Measuring Volume 1 (Archimedes’ Principle)

Let's take a look!

What type of experiment is this?

Experimental procedure and explanation:

• Let’s use the principle of buoyancy to measure the volume of objects, starting with those that sink in water.
• Place a container filled with water on the scale and reset the display to zero.
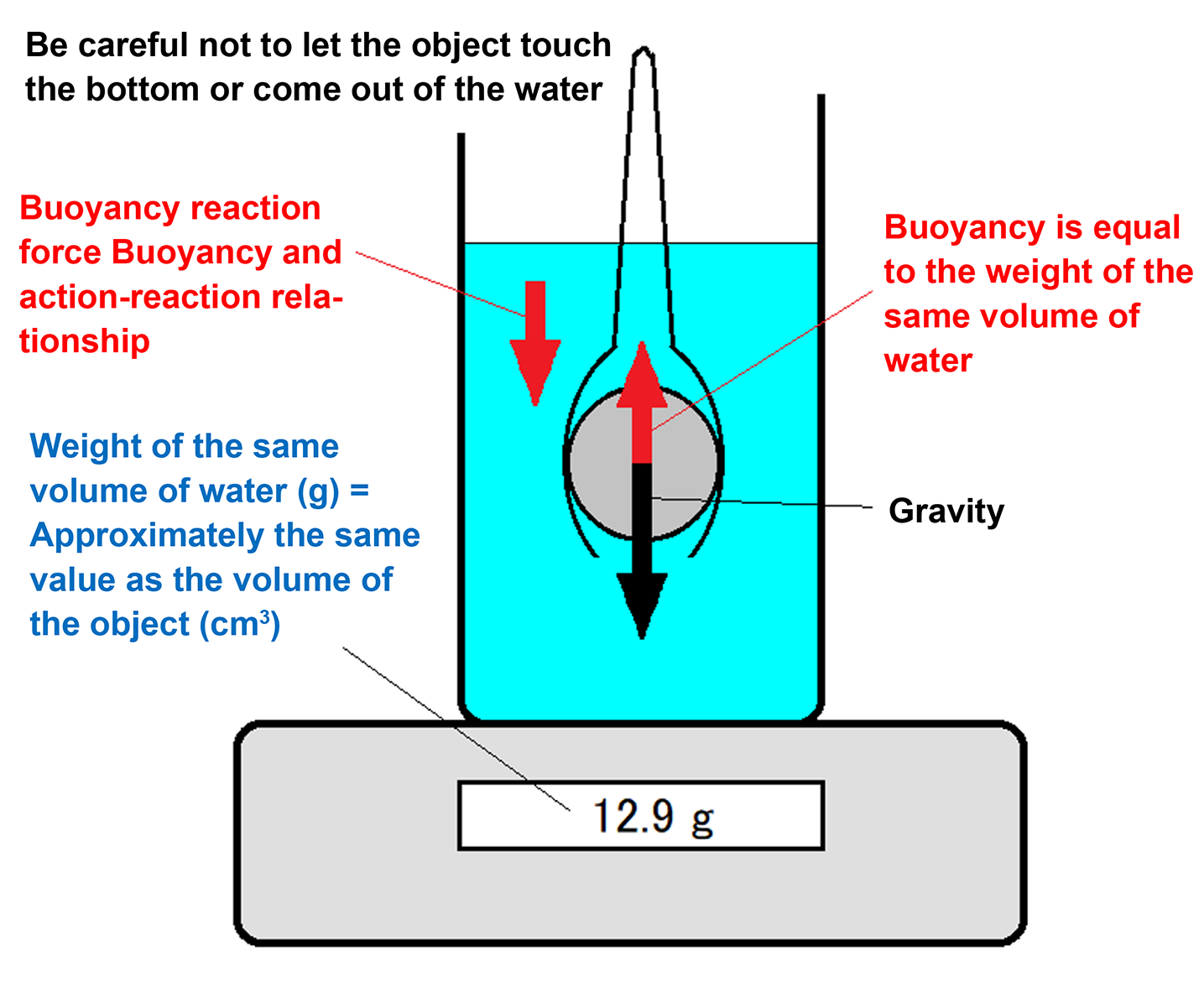
• First, measure the volume of the tongs. Submerge them to the marked line and note the weight displayed in grams. In this video, it reads 3.7 g. This means the submerged portion of the tongs has a volume of approximately 3.7 cm³. (Alternatively, you can reset the scale to zero with the tongs already submerged. However, when filming this video, my hand moved while holding the tongs, so I couldn’t zero the scale accurately. That’s why the method shown in the video was used.)
• This experiment demonstrates Archimedes’ principle, which states that the buoyant force acting on an object immersed in a fluid is equal to the weight of the fluid displaced by the object. In this case, the 3.7 g shown on the scale represents the reaction force to the buoyant force acting on the submerged object. According to Newton’s third law (action–reaction), this value is equal in magnitude to the buoyant force itself. Since the density of water is approximately 1 g/cm³, and the displaced water weighs 3.7 g (technically 3.7 gw, or gram-weight), the volume of displaced water is approximately 3.7 cm³. This means the volume of the submerged portion of the object is also approximately 3.7 cm³ because
  (displayed weight [g]) = (volume of water [cm³]) = (volume of object [cm³]).
  In conclusion, if the scale shows 3.7 g, the object’s volume is approximately 3.7 cm³.
• Next, grasp the object whose volume you want to measure using tongs or suspend it with a string. When immersing the object in water, ensure that it does not touch the bottom of the container, it is fully submerged (not floating above the water surface), and there are no air bubbles clinging to the object.
• Read the weight displayed on the scale (in grams). For example, if the display reads 16.6 g, and the buoyant force of the tongs alone was 3.7 g, then
  16.6 g − 3.7 g = 12.9 g, which means the object’s volume is approximately 12.9 cm³.
• Using this method, I measured the volume of a marble as 12.9 cm³ and the volume of the stone as 12.2 cm³.
• Next, measure the volume of a 10-yen coin. Because the volume of a single coin is very small, it is more accurate to measure the volume of multiple coins—in this case, 10 coins. Measuring a group improves accuracy. Since grasping multiple coins with tongs is difficult, use a small cup instead. Place 10 coins in the cup and submerge it in water while suspended. Be sure to carefully remove any air bubbles. Therefore, the volume of the 10 coins is
  6.5 g − 1.8 g = 4.7 g,
  which corresponds to a volume of 4.7 cm³ for 10 coins or 0.47 cm³ per coin.
• This video was produced with the support of the JSPS Grant-in-Aid for Scientific Research (18K03956).

[Keywords]	Buoyancy
[Related items]	Volume Measurement, Measuring Volume 2
[References]	Ryozo Ishiwata and Mitsumasa Nemoto, “The Wonder of Flow,” Kodansha Bluebacks, pp. 48–51. Ryozo Ishiwata, “Illustrated Fluid Dynamics Trivia,” Natsume Publishing, pp. 188–189.

Next　▶