Newsletter  2018.3  Index

Theme : "The Ninth JSME-KSME Thermal and Fluids Engineering Conference (TFEC9)" Preface T. HASHIMOTO，S. MATSUDA，H.J. Park How Turbulence Begins in a Transitional Flat-Plate Boundary Layer Yu FUKUNISHI, Yu NISIO, Seiichiro IZAWA (Tohoku University), Joe YOSHIKAWA (Industrial Technology Institute, Miyagi Prefectural Government) Numerical Simulation of Solidification and Deposition of Single Molten Droplet by Means of E-MPS Method S. KONDO, H. MAMORI (Tokyo University of Science), N. FUKUSHIMA (Tokai University), M. YAMAMOTO (Tokyo University of Science) Numerical simulation of a parallel plate particle separator for measurement of charging state of PM2.5 Takuto YONEMICHI, Koji FUKAGATA, Kentaro FUJIOKA, Tomoaki OKUDA（Keio University） Effect of viscoelastic Mach numbers on propulsive forces of a model helical flagellum in a viscoelastic fluid Kazuya TAJIMA, Fumihiko MIKAMI（Chiba University） Measurement of Ionic Current Fields by Using Variable Microgap Electrodes Takashi Fukuda, Kentaro Doi, Satoyuki Kawano (Osaka University)

 

Effect of viscoelastic Mach numbers on propulsive forces of a model helical flagellum in a viscoelastic fluid

Kazuya TAJIMA, Fumihiko MIKAMI Chiba University

Abstract

Some microorganisms propel themselves through the fluid by using rotating helical flagella, and many studies have been focused on the mechanics of swimming in purely viscous Newtonian fluids such as water. Recently, attention has been paid to the effects of viscoelasticity on the swimming of microorganisms, since many organisms commonly swim in complex fluid environments. In this study, we focused on the effect of viscoelastic Mach numbers M = V / c, where V is the speed of an object through a fluid and c is the speed of shear waves in the fluid. Joseph (1990) considered the problem of uniform flow of viscoelastic fluid past a body using a linearized theory and showed that a Mach cone will develop if M > 1, where the governing vorticity equation is hyperbolic when M > 1 and elliptic when M < 1. In this study, we examined experimentally the effect of viscoelastic Mach numbers on the propulsive forces of a rotating model helical flagellum in subcritical (M < 1) and supercritical (M > 1) conditions. Seven helical flagellum models with different pitches, helical diameters, and filament diameters were used for this study. The force measurement results show that the rotating speed dependence changes significantly at the speed whose Mach number based on the axial helical wave speed is unity. The propulsive forces are the function of only the tangential velocity along the helix when the tangential velocity is relatively high. The velocity fields obtained by a PIV (Particle Image Velocimetry) show that the flow patterns around a model helix with a larger pitch changes between subcritical and supercritical conditions.

 

Key words

Viscoelastic fluid, Viscoelastic Mach number, Helical flagellum, Propulsive force, Particle image velocimetry

 

Figures

Fig.1  Helical flagellum models for this study.

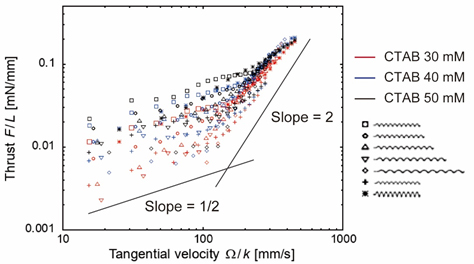
Fig.2  Thrust per unit filament length vs. tangential velocity.

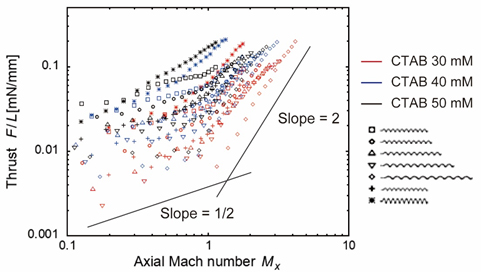
Fig.3  Thrust per unit filament length vs. axial Mach number.

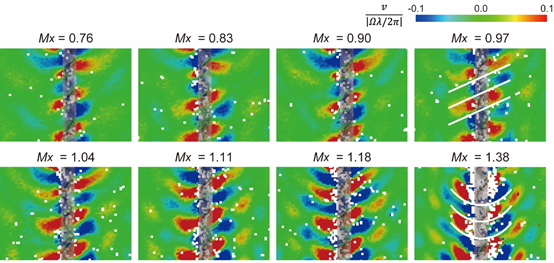
Fig.4  The axial component of fluid velocity generated by a rotating helical model (Model-E, 30mM)