Newsletter  2019.3  Index

Theme : "The Conference of Fluid Engineering Division" Preface (T. HASHIMOTO，S. MATSUDA，H.J. PARK) Development and launch of sounding rockets and development status of small launch vehicle by Japanese startup company Takahiro INAGAWA (Interstellar Technologies Inc.) Experimental quantification of friction drag reduction effects on an airfoil using uniform blowing Kaoruko ETO, Yusuke KONDO, Koji FUKAGATA (Keio University)and Naoko TOKUGAWA (Japan Aerospace Exploration Agency) Wind-tunnel experiments of friction drag reduction on an airfoil using passive blowing Shiho HIROKAWA, Kaoruko ETO, Yusuke KONDO, Koji FUKAGATA (Keio University)and Naoko  TOKUGAWA (Japan Aerospace Exploration Agency) A Study on Airfoil Flow and Aerodynamic Noise with Wake-boundary layer Interaction Noriaki KOBAYASHI　(The University of Tokyo) LES Analysis of Stator Cascade Flow in a Transonic Axial Compressor Seishiro SAITO (Kyushu University) Influence of grid resolution in large-eddy simulation of a turbulent pipe flow using the WALE model Daiki IWASA, Yusuke NABAE, Koji FUKAGATA (Keio University) The Dreams of Flow Contest Tomomi TERADA (Hokkaido University)   Separation of floating waste by "Water Surface Control Device" Toshiki HOMMA　 (Meisei University)

 

Influence of grid resolution in large-eddy simulation of a turbulent pipe flow using the WALE model

Daiki IWASA Keio University Yusuke NABAE Keio University Koji FUKAGATA Keio University

Abstract

CAE (Computer Aided Engineering) is an indispensable tool in the development of automobile engines. The Cross-ministerial Strategic Innovation Promotion Program (SIP) in Japan aims at improving the thermal efficiency of an internal combustion (IC) engines up to 50 percent and aims to reduce CO₂ emission by 30 percent, where an engine simulator, named HINOCA, is being developed so as to enable prediction and improvement of IC engines. As for the turbulence simulation in HINOCA, the wall-adapting local eddy-viscosity (WALE) model is adopted for the subgrid-scale model in large-eddy simulation (LES). However, in order to complete a simulation within a realistic computational time, it is inevitable to choose the grid spacing much coarser than that is well accepted. As for investigations of grid dependency for LES, many of the previous studies were done for a channel flow or in the streamwise and spanwise grid resolutions. Hence, there are many unclear points, especially in the wall-normal grid resolution. Therefore, we need to assess the accuracy of WALE model in the case where the computational grid is very coarse.

In the present study, we perform a comprehensive grid resolution study of WALE model in a turbulent pipe flow. The schematic of this computational domain is shown in Fig. 1. The LES is performed under the constant flow rate at the bulk Reynolds number of 5300. The governing equations are the filtered continuity equation and Navier-stokes equation. A top-hat filter is used for the spatial filter.

Figure 2 shows mean streamwise velocity and RMS velocity fluctuations in the case of (N_r, N_θ, N_z) = (6, 64, 64). If the grid spacing in the wall-normal direction is non-uniform, the velocity and RMS velocity fluctuations are in good agreement with those of DNS. However, if we adopted uniform grid spacings, the turbulent statistics do not agree. Especially, the values at the first grid point from the wall substantially deviate from the correct values. Streaks for LES at y⁺ = 20 shown in Fig. 3(b) are somewhat similar but somewhat different form that of DNS, as shown in Fig. 3(a). The streak length obtained by LES are smaller than that of DNS. Therefore, it is confirmed that although the turbulent statistics such as the mean velocity profiles and the second order moments is reproduced by LES with less grid points, the streak structures largely affecting the flow dynamics in the bulk region cannot be reproduced accurately. Figure 4 shows the relationship between the wall-normal location of the first grid point and the turbulent statistic values at the first grid point in the case of (N_θ, N_z) = (64, 64). From Fig. 4(a), it is found that the velocity at the first grid point is on the line of u⁺ = y⁺. Moreover, if the first point is located within y⁺ < 6, the velocity agrees with that of DNS. On the other hand, from Fig 4(b), the values of RMS streamwise velocity at the first grid point distribute along to the profile of DNS if the first grid point y⁺ < 6. Above that, however, the RMS value is gradually decreased. Hence, it is impossible for the first grid point to capture the peak value of RMS streamwise velocity.

Key words

Grid resolution, Large-eddy simulation, Turbulent pipe flow, WALE model, HINOCA.

Figures

Fig. 1: Computational domain for numerical simulations of a turbulent pipe flow.

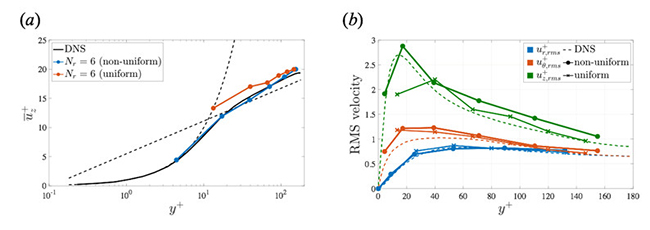
Fig. 2: Turbulent statistics using only 6 points with uniform or non-uniform grid spacings in the wall-normal direction. (a) Mean streamwise velocity profiles (solid lines with markers) and the law of the wall (dashed line); (b) RMS velocity fluctuations.

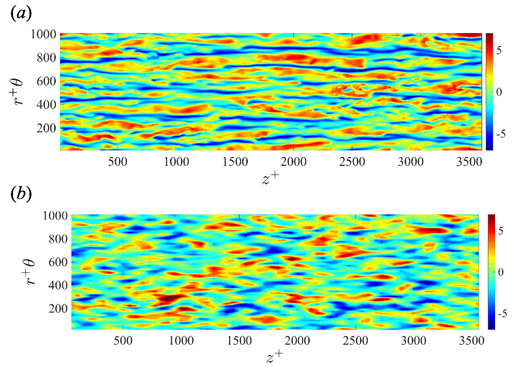
Fig. 3: Instantaneous streamwise velocity fluctuation contours at y⁺ = 20 in the turbulent pipe flow. (a) DNS; (b) LES in the case of (N_r, N_θ, N_z) = (6, 64, 64).

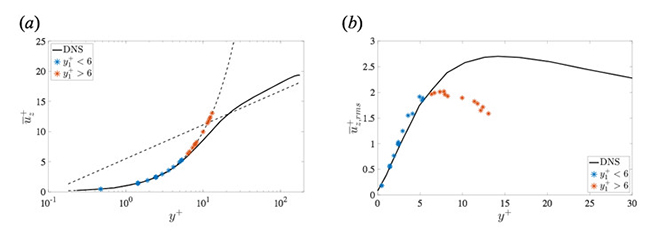
Fig. 4: Relationship between the wall-normal location of the first grid point from the wall and the resultant values of turbulent statistics there: (a) mean streamwise velocity; (b) RMS streamwise velocity fluctuations.