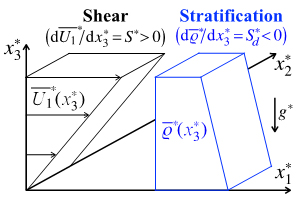
Figure 1 Sketch of the mean field.
Activities
Home > Activity > Newsletter > 2021.3
Theme : "The Conference of Fluid Engineering Division (March issue)”
|
Aoi NAKAMURA,
|
Unsteady turbulence under uniform stratification and uniform shear is analysed by direct numerical simulations (DNS) at a moderate Reynolds number (Re = 50) and a Prandtl number Pr = 1, to investigate the combined effects of stratification and mean shear, and discuss the applicability of the rapid distortion theory (RDT). Numerical scheme for the present DNS is the Fourier-spectral method. The computational domain is much larger than the initial integral scale to resolve the large-scale structures which develop in stratified shear flows. The stratification and shear have linear effects on the flow since the buoyancy term and the mean-shear term are the linear terms in the governing equations. They have more significant effects on large scales, and the stratification is effective down to the Ozmidov scale, and the mean shear is effective down to the Corrsin scale. Then, the RDT, which is a linear theory, applies down to the Ozmidov or Corrsin scale. The DNS results also show that the mean shear enhances the large-scale motion and suppresses the small-scale vertical motion, leading to a better applicability of RDT even at small scales.
Turbulence, Stratified Flow, Shear, Ozmidov Scale, Corrsin Scale

Case |
Sh | Fr | L (DNS) |
Sh1Fr1 |
1 | 1 | 30π |
Sh1Fr01 |
1 | 0.1 | 30π |
Sh10Fr1 |
10 | 1 | 30π |
Sh10Fr01 |
10 | 0.1 | 40π |
Sh15Fr01 |
15 | 0.1 | 40π |
Sh20Fr01 |
20 | 0.1 | 40π |
Sh30Fr01 |
30 | 0.1 | 40π |
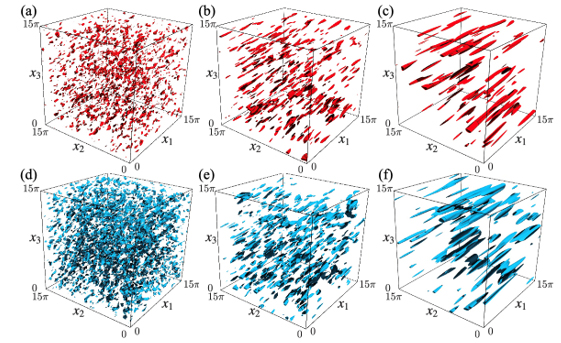
Figure 2 Distribution of the kinetic energy ui2/2 (red) and the potential energy ρ2/(2Fr2)(blue) obtained by DNS (Case Sh1Fr1). (a,d) t=U*0t*/L*0=2, (b,e) t = 10 and (c,f) t = 20.
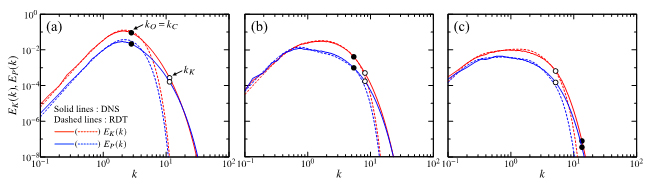
Figure 3 DNS and RDT results of the kinetic-energy spectrum EK(k) and the potential-energy spectrum EP(k) at (a) t=1 , (b) t=4 and (c) t=8 for Sh1Fr1. The symbol ● on the solid lines (DNS) indicates the Ozmidov wavenumber kO=lO-1 which is equal to the Corrsin wavenumber( kC=lC-1 ), and ○ indicates Kolmogorov wavenumber kK=lK-1 (l*K=(ν*3/ε*)1/4: Kolmogorov scale).
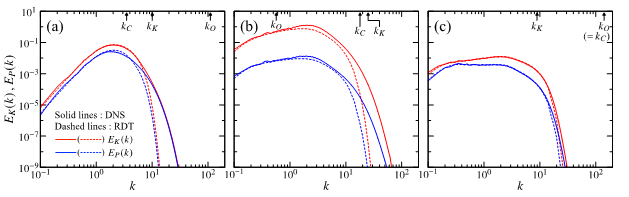
Figure 4 DNS and RDT results of the kinetic-energy spectrum EK(k) and the potential-energy spectrum EP(k) at t=1.5 for (a) Sh1Fr01, (b) Sh10Fr1 and (c) Sh10Fr01. The arrows at the top of each figure indicate the Ozmidov, Corrsin and Kolmogorov wavenumbers.
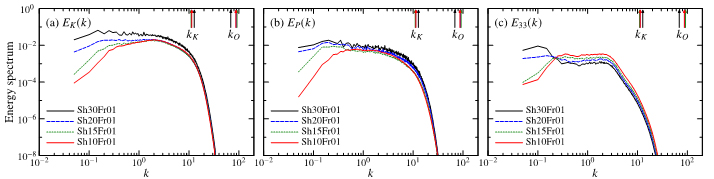
Figure 5 Shear-parameter dependence of the energy spectra (a)EK(k), (b)EP(k) and (c)E33(k) at t=1 obtained by DNS. The arrows at the top of each figure show the four Kolmogorov wavenumbers and four Ozmidov wavenumbers corresponding to the four simulated cases. The Corrsin wavenumber satisfies kC ≥ kO (kC = Sh3/2Fr3/2kO) in all the figures.