流れ 2003年8月号 目次
― 特集：混相流 ―
｜ リンク一覧にもどる ｜ |
固気二相自由乱流の渦法シミュレーション
 名古屋大学 情報メディア教育センター 内山知実 |
１．はじめに
気流中に微細な固体粒子を含む自由乱流は，化学プラントやエネルギー機器など様々な工業装置において見受けられる．固気二相噴流はその代表例であり，これまでｋ－ε二方程式モデルによる解析[1]が行われてきたが，最近では
DNS[2]やLES[3]が実行され，流れの発達過程や運動量拡散に及ぼす粒子の影響など，実験的研究を補完し得る貴重な知見が得られつつある．
一方，渦法が様々な流れ場の数値解析に有効に利用され，とくに組織的な大規模渦が支配的な単相自由乱流の解析に多用されている．渦法は，渦度場を多数の渦要素で離散化し，要素の挙動を追跡して流れ場を求めるLagrange型解法であり，渦の形成や変形など渦構造の発展過程を直接計算できるためである．著者は，渦法の適用範囲を拡大するため，固気二相自由乱流に対する二次元渦法を提案し[4]，二次元混合層[5]，スリットノズル噴流[6]および物体後流[7]の二相流解析に適用し，解法の妥当性を示した．また，自由空間中を自由落下する粒子群が形成する粒子噴流の解析にも適用した[8]．最近では，固気二相同軸円形噴流に対する三次元渦法を提案した[9]．
本稿では，自由落下粒子群が形成する粒子噴流および同軸円形噴流の解析例を紹介する．
２．自由落下粒子群が形成する粒子噴流の二次元解析[8]
自由空間中を粒子群が落下する場合，周囲の自由空気が粒子群に巻込まれ，粒子を含む下降気流が発生する．このような粒子噴流は粉塵の飛散などの原因となるため，実験的研究が多数遂行されてきた．ここでは，ガラス粒子（密度2590
kg/m3）を二次元スリットから質量流量3 g/sのもと自由落下させた場合を対象として，図１のような体系のもと二次元解析した．
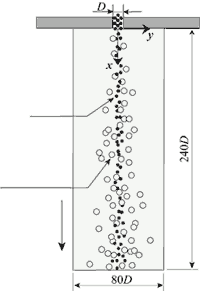
図１ 粒子噴流の概略
直径400μmの粒子を落下させたときの粒子分布を図2に示す．ただし，落下開始から10秒後の結果である．後述するように巻込み空気の流れが存在するにもかかわらず，粒子はオリフィス出口から直線的に落下し，横方向へ広がらない．解析の対象とした粒子は慣性力が大きいため，いずれの時刻においても同様に分布する．
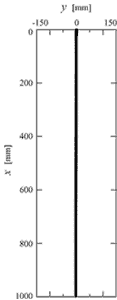
図２ 粒子の分布
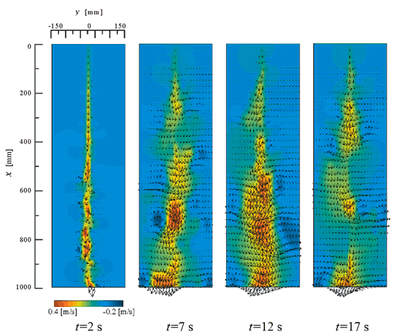
図3は空気速度分布の時間変化を示す．t
= 2 sでは，粒子が存在する中心軸近傍においてのみ下降流が存在する．時間が経過すると，巻込み空気の流れが規模を増し，大きな渦が中心軸の左右に交互に現れる．t=12および17
sでは中心軸上の速度が増すとともに渦が大きくなり，発達した噴流が形成される．
水平断面を通過する空気の流量すなわち巻込み空気流量Qは，空気の平均速度を断面内で積分すれば求められる．直径が300，400，500μmの粒子が落下するときのQと落下距離xとの関係を図4に示す．Qはxの増加とともに増し，解析モデル（Massive
particle model）の予測結果とほぼ一致している．
（画像をクリックすると動画612KBがご覧になれます）
図３ 空気速度分布の時間変化（アニメーション）
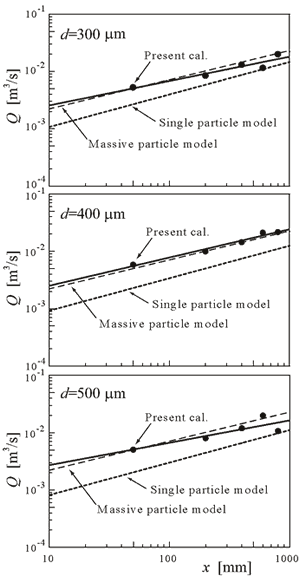
図４ 巻込み空気流量の軸方向変化
３．同軸円形噴流の三次元解析[9]
速度υa の一様流中におかれた円形ノズルから一様流と同一方向に速度υ0で噴出する同軸円形噴流（図５参照）の解析例を示す．ただし，流れは鉛直下向きであり，υ0 に基づくReynolds数が20000，速度比 υa /υ0が0.27の空気噴流に，ガラス粒子（直径100μm）がノズルから質量混合比0.27で供給される．粒子のノズル出口速度は0.8υ0 ，Stokes数は200である．
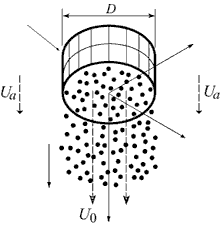
図５ 同軸円形噴流の概略
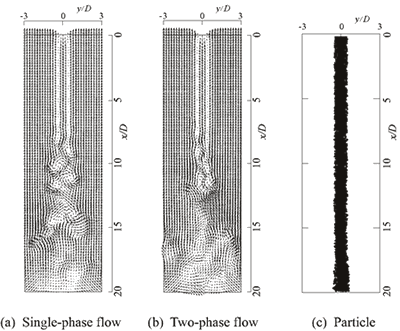
鉛直断面内の気相速度と粒子の分布を図６に示す．ただし，平均速度を差し引いた速度ベクトルと全粒子を断面内に投影した結果が表示してある．単相流時には
x / D 
7.3
において大規模渦が発生し，下流ほど規模が増し半径方向に拡散する．二相流時には，単相流時に比べ，ポテンシャルコア消滅後の速度の広がり幅が狭く，とくに
10 
x
/ 15
で顕著である．半径方向への気相運動量の拡散が粒子により阻害されている．このような結果は，円形噴流のDNS[2]やスリット形噴流の二次元渦法解析[6]でも求められている．一方，粒子はStokes数が大きいため，大規模渦の影響をほとんど受けず，直線的に運動する．
（画像をクリックすると動画1612KBがご覧になれます）
図６ 気相速度と粒子の分布
図７は等渦度面の分布を示す．ポテンシャルコアの消滅直後に螺旋状の等渦度面が現れる．二相流時には 8 x
/ D 12
において螺旋の振幅が減じている．
噴流中心軸上の気相および粒子の平均速度を求め，軸方向に対する変化を示すと図８のようになる．二相流時の気相速度は，単相流時と比較すると，
7 x
/ D 12
でやや低い．気相よりも低速度でノズルから噴出する粒子が気相に抗力を及ぼすためである．しかし，x
/ D > 12 では単相流時よりも高く，下流方向への速度減衰が緩和される．減速することなくほぼ一定速度で運動する粒子が気相に運動量を付与することに起因している．このような速度減衰の緩和は，円形噴流の実験[10]やDNS[2]，スリット形噴流のLES[3]や二次元渦法解析[6]でも報告されている．
（画像をクリックすると動画1119KBがご覧になれます）
図７ 等渦度面（ |
ω
| / | ω | = 0.1 ）の分布
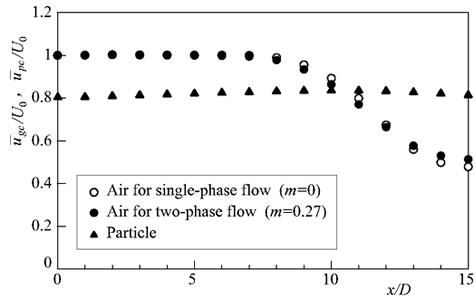
図８ 中心軸上速度の軸方向変化
４．おわりに
渦法による固気二相自由乱流の解析例を紹介した．ここでは省略したが，スカラーポテンシャルとベクトルポテンシャルにより気相速度場を表現するVortex
in Cell法に準拠した二相流解法も提案されている[11]．
本解法は渦法の特徴を生かしたLagrange型解法でありながらも，Two-way couplingの計算の一部に流れ場を格子に分割するEuler的手法を援用している．今後，格子を用いることなくTwo-way
couplingを実現できる，完全Lagrange型解法の開発が重要な課題と考えられる．
参考文献
[1] Elghobashi, S., ほか3名, “Prediction of the particle-laden
jet with a two-equation turbulence model,” Int. J. Multiphase
Flow 10-6(1984), 697.
[2] 湯晋一・ほか2名, “三次元固気混相乱流自由噴流のTwo-Way Methodを用いた直接数値計算と実験による検証,”
日本機械学会論文集 60-572 B(1994), 1152.
[3] 湯晋一・ほか2名, “高レイノルズ数スリットノズル固気混相噴流の流れに与える粒子の影響,” 日本機械学会論文集
66-641 B(2000), 57.
[4] 内山知実・ほか2名, “渦法による固気二相自由乱流の数値解法（数値モデルと二次元混合層への適用）,”
日本機械学会論文集 66-651 B(2000), 2853.
[5] Uchiyama, T. and Naruse, M., “Numerical simulation
of gas-particle two-phase mixing layer by vortex method,”
Powder Technol. 125(2002), 111.
[6] Uchiyama, T. and Naruse, M., “Vortex simulation of
slit nozzle gas-particle two-phase jet,” Powder Technol.
131(2003), 156.
[7] Uchiyama, T. and Yagami, H., “Numerical simulation
of wake gas flow laden with solid particles,” Proc. 2nd
Asian Particle Technol. Symp., Penang, (2003), (on CD-ROM).
[8] 内山知実・北野佳伸, “自由落下粒子群が形成する粒子噴流の数値解析,” 日本機械学会論文集 69-684
B(2003),（印刷中）.
[9] Uchiyama, T. and Fukase, A., “ Three-dimensional vortex
simulation for gas-particle two-phase compound round jet,”
Proc. 2nd Asian Particle Technol. Symp., Penang, (2003),
(on CD-ROM).
[10] 菱田公一・ほか2名, “固気二相軸対称噴流の乱れ構造,” 日本機械学会論文集 51-467 B(1985),
2330.
[11] 内山知実・成瀬正章, “Vortex in Cell法による固気二相自由乱流の数値解析（数値解法と二次元混合層への適用）,”
日本機械学会論文集 B(2003), （印刷中）.