流れ 2009年9月号 目次
― 特集テーマ： 特集テーマ： 界面を含む流れのシミュレーション ―
｜ リンク一覧にもどる ｜ |
界面体積追跡法の最近の進展とサブクール沸騰解析への展開
|
1. 界面体積追跡法の最近の進展
一般に変形する自由界面を伴う流れを解析する場合，界面における表面張力効果を正確に考慮する必要があり，このため界面曲率や界面を通過する流体輸送量を精度良く計算することが重要である．従来から，自由界面を含む流れ解析の一つの典型である気泡流の解析では，界面を一種の膜としてその挙動を境界積分法1)で追跡する手法，自由界面形状を精度良く追跡するために計算格子を界面変形に追従させながら解析する有限要素法2)，境界適合座標系3)，Lagrangian法4)等の適用が試みられているが，いずれの方法も界面追跡のために計算格子の頻繁な再構成が必要であり，その際に数値誤差や数値不安定を発生する可能性がある．一方，このような計算格子の再構成を必要としない解析手法として，MAC(Marker and Cell)法5)やFront-tracking法6)に代表される質量を持たないマーカー粒子を追跡して界面形状を追跡する方法があるが，流体の渦運動のために一部のマーカー粒子の凝集や，界面近傍の粒子が不足して界面が決定できないなど，粒子数の保存や粒子再配置等についての人為的な制御が必要となる．特に，界面が合一・分裂するような場合には界面近傍の粒子の制御は極めて困難である．最近では，流体運動を多数の粒子間相互作用としてモデル化して取扱うMPS(moving particle semi-implicit)7)，界面捕獲に距離関数を用いるLevel-set法8)や密度関数の輸送を用いるCIP(Constrained Interpolation Profile)法9)などが研究されている．これらの手法はそれぞれ特長を有するため，手法の優劣を決定することは不可能である．したがって，本稿では，気液各相の体積保存性に優れるため気液二相流現象への適用性が高い界面体積追跡法について最近の進展を概観し，相変化を含む気液二相流系への展開について紹介する．
界面体積追跡法の代表格はVolume-of-fluid法10)であり，以下の流体率輸送方程式によって界面追跡を行う．
ただし，f は流体率であり，各計算セルにおける液相領域の割合を示す．また，
は速度ベクトルである．Volume-of-fluid法は，界面セル（界面を含む計算セル）における界面再構築の有無によって大別され，再構築を行わない手法としては，Donor-Acceptor法による流体率輸送を行うSOLA-VOF法11)，高解像度スキームによる流体率輸送を行うFCT-VOF法12)およびCICSAM（Compressive Interface Capturing Scheme for Arbitrary Meshes）法13)などがあり，再構築を行う手法としては，界面を水平もしくは垂直面として表すSLIC（Simple Line Interface Calculation）法14)や界面勾配を考慮するPLIC（Piecewise Linear Interface Calculation）法15)などがある．これらのうち，PLIC法は幾何学的計算を含むため比較的複雑な計算アルゴリズムを必要16)とするが，一般的に最も高精度な解を導く．PLIC法の計算手順は，1）界面勾配ベクトル（界面に垂直な単位ベクトル）の計算，2）界面の再構築（各界面セルにおける界面勾配の接続性），3）流体率の輸送であり，各手順に対して様々な計算手法が提案されている．界面勾配ベクトルの計算に関しては，注目する界面セルの周囲の流体率分布から計算する比較的簡単な手法17)， 2次精度の計算手法であるLVIRA（Least Square Volume-of-fluid Interface Reconstruction Algorithm）法18)等がある．界面の再構築に関しては，従来の（Newton-Rapthon法などを用いた）反復計算法に加え，より高速で高精度な直接計算法19)が提案されている．また，流体率の輸送に関しては，各座標軸方向の輸送を別々に行うOperator-splitting法，各方向の輸送を同時に行うため高精度な解が得られるmulti-dimensional法があり，後者については，更なる高精度化のため，流線に沿った流体率積分を行うStream法20)や幾何学的な予測・修正を行うGPCA（Geometrical Predictor-corrector Advection）法21)等が提案されている．ただし，検証問題の解析結果を見る限り，流体率の輸送を高精度化することによる解析精度向上は限定的である．PLIC系の手法は様々な気液二相流現象解析に適用され，高精度な解を導くことが確認されており22)，最近では非構造格子系におけるPLIC法の高精度解析手法が提案されている23)．その他，PLIC法をLevel-set法と組み合わせたCLSVOF（Coupled Level-set and Volume-of-fluid）法24)やMarker法と組み合わせた手法25)，1つの界面セル内において複数の界面を考慮できる手法26)などが検討されている．
気液二相流現象の高精度解析のためには，界面における物理現象を正確にモデル化する必要がある．特に，表面張力モデルの誤差によって誘起されるSpurious Velocityの抑制に関して多くの研究が行われている．一般に，Volume-of-fluid法を用いた数値解析では，界面上の表面張力(面積力)を界面セル内で積分した体積力としてNavier-Stoke方程式（運動量輸送式）のソース項として考慮する．その際，流体率分布から界面曲率を計算する必要があり，古典的なCSF（Continuum Surface Force）モデル27)では，流体率の勾配・発散から界面曲率を計算するが，計算精度がそれ程高くないため，例えばEstimator Functionを用いた手法28)や局所界面形状を二次曲面で近似するPROST（Parabolic Reconstruction of Surface Tension）モデル29)が開発され，Spurious Velocityを大幅に抑制することに成功している．また，最近では，界面からの距離関数を再構築して界面曲率の計算を行うRDF（Reconstructed Distance Function）モデル30)やHeight Functionを用いて計算を行う手法24)を用いた高精度化が検討されている．Spurious Velocity抑制のためには，高精度界面曲率計算手法に加え，Navier-Stokes方程式における圧力項および表面張力項の定式化が重要である．一般的には，正しい界面曲率の値を用いた場合においてもSpurious Velocityが発生することが知られている．これを防止するためには界面セルで圧力と表面張力がバランスする必要があり，Balanced-force Algorithm31)と呼ばれる定式化を用いることで，Spurious Velocityの抑制に関して高精度の界面曲率計算手法と同等以上の効果があることが明らかになっている32)．また，局所的な界面変形挙動の解析精度を向上させるため，解適合格子におけるVolume-of-fluid法34)やPLIC法の拡張34)および，非構造解適合格子の開発例35)もある．著者らも非構造解適合格子系PLIC法の開発を進めており，少ない計算セル数で高精度な解が得ることを確認している．その一例として，高速炉のガス巻き込み現象の予測をターゲットとした解析例36)を図1に示す．これは，一様流中に角柱を置き，その角柱後流に吸い込み管を設置した場合のガス巻き込み現象の解析結果をレイトレーシングで表現したものである．
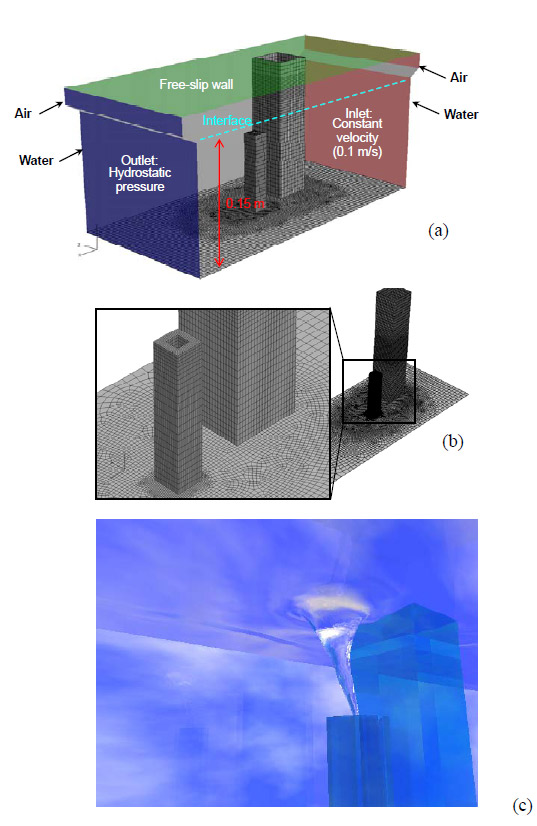
図1 一様流中の角柱後流に設置した吸い込み管によるガス巻き込み現象解析36)
(a) 解析体系
(b) 解析体系の非構造格子分割例
(c) ガス巻き込み解析例(レイトレーシング表現)
2．サブクール沸騰解析への展開
沸騰現象は，理論的な取扱いや実験による直接的な現象観察が極めて困難であるため，これまでは膨大な実験データに基づく経験的なパラメータを導入した実験式や経験式に依存するモデル化が一般的である．一方，筆者らは上述の界面体積追跡法に基づく混相流数値解析法を用いて，沸騰時の伝熱特性やその詳細なメカニズムを解明するための沸騰・凝縮モデルの構築を目指した研究を行っている．特に，飽和沸騰と比較して高い熱流束が得られるサブクール沸騰（飽和温度とバルク液温との差，すなわち，過冷度が大きい場合の沸騰現象）に着目している．本節では，沸騰・凝縮モデルの概要および著者らが開発したMARS（Multi-interface Advection and Reconstruction Solver）22)に沸騰・凝縮モデルを組込み，サブクール・プール沸騰における気泡挙動の3次元数値シミュレーション結果例について紹介する．
ここで検討している沸騰・凝縮モデルは，Rayleigh-Taylor不安定の状態にある過熱液を仮定した均一核生成理論に基づく核生成モデルと，核生成後の気泡成長・凝縮モデルの2段階から構成される37)．気泡成長・凝縮モデルは，温度回復法（エンタルピー法）38)を基にした相変化モデルと，発生気泡内のγ則気体の等エントロピー変化を仮定した膨張・収縮モデル37)を用いている．ここで，相変化モデルは水‐蒸気系のように気液相変化時の大きな密度変化を適切に取扱うための修正を施している39)．本モデルによる相変化計算手順は，界面セルに対して，１）相変化を考えず温度場の計算を行う，２)飽和温度からの温度差に相当する顕熱量と相変化に伴う潜熱量との比を相変化率として計算し，その変化率を気相または液相の流体率に反映する，３）相変化により界面セルの温度を飽和温度に回復する．
本モデルは相変化について状態方程式の熱力学的変化を評価するのではなく，「準静的熱平衡過程」の仮定に立って，潜熱量と顕熱量の交換をモデル化して相変化過程を取扱う．したがって，「準静的熱平衡過程」の気液界面を含んだ計算格子内での相変化は瞬間的に生じる（すなわち，気液界面の厚みはゼロ）．しかしながら，この過程だけでは準静的熱平衡過程のうちの「無限にゆっくりと変化する」過程が無視されている．そこで，気液界面の厚みを考慮する，すなわち，界面領域での非定常熱伝導効果を検討した．このため，相変化に伴う移動界面が界面セル内を通過する特性時間，すなわち「緩和時間」の概念を非定常熱伝導の観点から新たに導入した．この緩和時間の導入により，界面セル内の相変化は単位時間あたりに界面セルの70％だけ進行することを解析的に見出した40)．この緩和時間は相変化モデルを適用する界面セルの流体率F (0≤ F ≤1)の制約条件(30%)として導入するだけで考慮できる，すなわち，相変化の開始を遅らせたり(例えば， F ≥0.15)，または終了を早めたり(例えば，F ≤0.85)できる．
以下では，本モデルをMARSに組み込み，サブクール・プール沸騰で発生した気泡挙動の3次元数値シミュレーションに適用した例を示す．計算条件はモデル検証用に大気圧条件下で実施された可視化実験41)に合わせ，サブクール度ΔTsubが10.3K，伝熱面からの熱流束q は0.25W/mm2とした．また，核生成モデルによって直径6µmの気泡核（推定した伝熱面過熱度10Kに相当）を伝熱面中央に1個配置して計算を開始した．図2に示した可視化実験によれば，気泡が伝熱面から離脱する際，サブクール度が10K程度になると，気泡は水平方向に扁平へと成長した後，今度は縦長に強く伸長してから伝熱面より離脱する傾向にある．図3はシミュレーション結果であるが，核生成後の急激な成長は可視化出来ないが,その後に気泡が水平方向に扁平となり，次いで表面張力による復元力が大きく作用している観察結果と定性的に一致している．図4は気泡成長段階のシミュレーション結果（速度ベクトルと界面等高線）を示しているが，水平方向への気泡の成長に伴い，気泡底部と伝熱面との間に薄い液相が取り残されていく様子が確認できる．これは，沸騰熱伝達の伝熱機構に非常に大きな影響を及ぼすと言われている薄液膜（マイクロレイヤー）42)の存在を示唆するもので，本モデルにおいて相変化時の緩和時間を考慮したことにより，計算格子内に蒸発せずに残留している液相が薄液膜として顕在化したものではないかと推測される．また，気泡成長に伴う気泡端から気泡内部へ流入する強い流れによって，気泡周囲の液膜が気泡内部に引き込まれる様相も見られる．これらの現象については，まだ十分な考察が行われていないため，更なる検討が必要と考えられるが，実験相関式を用いずに沸騰現象をシミュレートできたことは，今後の進展に大きな意味を含んでいると思われる．本例では，伝熱面上に1個の気泡核を配置した孤立気泡を対象としたが，実際の現象では伝熱面上に多数の気泡核が存在していることは明らかであり，今後は伝熱面上の発泡点密度をモデル化し，多数の気泡同士が干渉する沸騰ニ相流動場に対しても適用・検討していく必要がある。さらに，乱流との相関関係についての検討を行うことも課題として残されている．最終的には，強制対流沸騰における流動様式の予測やDNB及びドライアウトの限界熱流束の発生機構の予測に繋がることを期待している．
図2 サブクール沸騰気泡の離脱挙動の高速度カメラによる可視化像
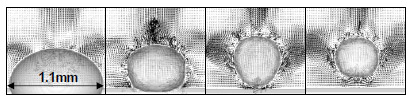
図3 サブクール沸騰気泡の離脱挙動の数値解析結果
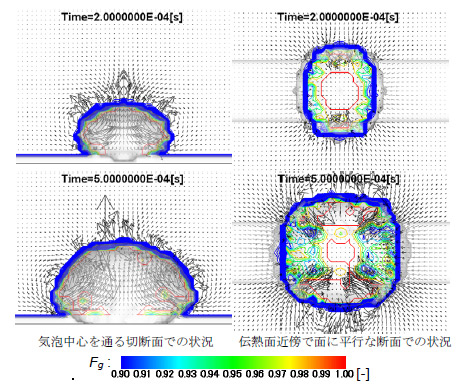
図4 サブクール沸騰気泡の成長過程シミュレーション結果の一例
（気泡は加熱白金細線の上で形成．下側の図では伝熱面上に液膜の残留が認められる）
参考文献