流れの読み物

Home > 流れの読み物 > ニュースレター > 2014年12月号

流れ　2014年12月号　目次

―　特集テーマ：2014年度年次大会 (2)　―

  1. 巻頭言
    （真田，横山，杵淵）
  2. 高クヌッセン数流れ（希薄気体流からマイクロ気体流れへ）
    新美智秀（名古屋大学）
  3. ワークショップ：先端熱流体計測の計算との連携を含む新展開
    早瀬敏幸（東北大学）
  4. 荷電ナノ粒子流の計測（イオン電流とトンネル電流）
    土井謙太郎，川野聡恭（大阪大学）
  5. 空力音源探査のためのファン表面圧力変動計測技術の開発
    飯田明由（豊橋技科大）
  6. プロセス・トモグラフィー法による血液循環流路内の血栓検出の可能性
    Sapkota Achyut，布施拓士（千葉大学），丸山修（産業技術総合研究所），武居昌宏（千葉大学）
  7. 最近の先端熱流体計測における高速度カメラの利用について
    桑原譲二（株式会社フォトロン）

 

荷電ナノ粒子流の計測（イオン電流とトンネル電流）


土井 謙太郎
大阪大学　

基礎工学研究科


川野 聡恭
大阪大学　
基礎工学研究科

 

はじめに

　 近年，マイクロ・ナノ流路を用いた流れ場の制御と単一分子の検出・識別技術に関する研究開発が注目を集めている[1]–[5]．特に，デオキシリボ核酸（DNA）やリボ核酸（RNA）の塩基配列を超高速に解読するための革新的技術につながるとして期待されている[2],[3]．DNAやRNAなどの長鎖高分子は，液中で糸まり状の構造で安定に存在するため，それを解きほぐしながら直線状にした後に，一塩基ずつ識別する必要がある[4],[5]．そのために，流路のサイズを段階的に絞りながら分子を誘導し，最終的には直径10 nm以下のナノポア（その内壁にナノギャップ対電極を備えた孔状流路）の中で一塩基分子を電気的に識別するといった一連の手順が提案されているが，各プロセスにおいて未だ課題が残されている．特に，ナノ流路における流動場と分子の振る舞いについては未知の部分が多く，現象の解明について実験と理論の両面からアプローチが必要とされている．我々はこれまで，DNAのモデル化[6],[7]とナノ流路における分子流動シミュレーション[8]を行うとともに，ナノポアに設置されたプローブ電極による単一粒子の電気的検出メカニズムに関する理論解析[9],[10]を行ってきた．また，図1に示すようなナノギャップ対電極を備えた矩形流路を開発し，実験結果との比較検討を重ねることによる理論解析手法の高精度化を目指してきた[11],[12]．マイクロ・ナノ流路において，支配的に存在する電解質イオンの移動と帯電した分子やナノ粒子の運動を識別するためには，両者を異なる方法で計測する必要がある．一手段として，イオン電流とトンネル電流を用いて分離識別する方法が提案されている．すなわち，図2に示すように，分子や粒子がナノポアに入ると流路に沿った電解質イオンの輸送が妨げられるためにイオン電流は減少するが（図2(a)），ナノギャップを持つ電極間に物体が存在するときにトンネル電流は増加する（図2(b)）．本稿では，イオン電流とトンネル電流を用いた一粒子計測技術に関する現状について紹介する．


Fig. 1. Scanning electron microscope image of (a) nanogap pair electrodes embedded in nanochannel and (b) magnified view of the nanogap, in which ion current flows along the nanochannel and tunnel current passes across the nanogap between the electrodes [12].


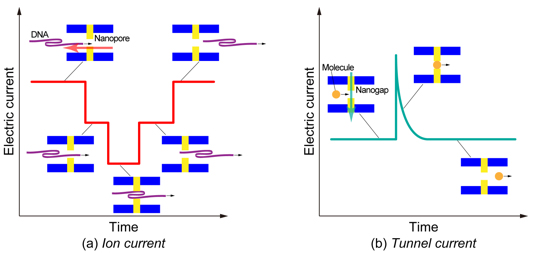
Fig. 2. Schematic illustrations of (a) ion current and (b) tunnel current in single molecule detection.

 

１．イオン電流とトンネル電流による分子およびナノ粒子の識別

１．１．イオン電流

　電解質溶液中を電荷が移動するとき，電極間にイオン電流が観測される．電荷の担体として，電解質イオン，帯電した分子および荷電粒子などが挙げられる．電極間に電場を印加すると，平衡状態で一様に分布している正負の電解質イオンが各電極に引かれるとともに濃度勾配による拡散が生じ，加えて電極表面で酸化還元反応を伴う場合は，定常電流が得られる．このような，電気泳動と拡散に起因するイオン電流は，Nernst–Planck方程式およびPoisson方程式を自己無撞着に解くことにより調べることができる[13]．さらに移流を含む場合には，Navier–Stokes式も同時に解いて速度場を求める必要がある．DNA分子やナノ粒子は，そのような流れ場を電気泳動等によって移動するが，これら検出対象は，電解質イオンに比べて濃度が非常に低いため，マイクロ流路ではイオン電流のノイズに埋もれて電気的に検出することはできない．そこで，溶液中の対象粒子をイオン電流の応答から検出するために，マイクロ流路に粒子サイズと同程度の径を持つナノポアを設置すると，粒子の通過に伴う排除体積効果によりイオン電流の減少が観測される（図2(a)）[11],[12]．この原理は，Coulter counterとして知られてきたが，MEMS/NEMSプロセスを用いることにより多様なサイズの粒子検出に適用可能となってきた．しかしながら，高分子を構成するモノマーのサイズについては，イオン電流で識別できるまでには至っていない．

１．２．荷電粒子の電気計測

　1 nm以下の単一分子を識別するために，量子効果であるトンネル電流を用いる手法が提案されている．前述の流路構造において，ナノポア内部に分子サイズのギャップを持つ微小電極を配置し，そこに分子または粒子を捕捉しながら電圧を印加すると微弱ではあるが電流が検出されることが知られている[1]–[3]．これが量子力学効果による電流であるとする理由は，電極間に分子が存在することによって電流値が増加するところにある（図2(b)）．イオン電流の場合は分子や粒子の存在がイオン電流を妨げる抵抗となるが，トンネル電流の場合はむしろ伝導性を向上させる要因である．一般的に，トンネル電流の値は距離に対して指数関数的に減衰すると考えられるが，電極間に分子やナノ粒子が存在する場合は，量子力学的意味で電極ギャップが短絡するために導通することになる[10]．

　 ただし，検知電流が増大する要因としてはトンネル電流のみでなく，電極のキャパシター化効果（荷電粒子の電極への衝突による電荷蓄積とその瞬時放出）による可能性も高いと考えられるため，実験結果の評価には多角的な検討が必要となる．たとえば，我々の先行研究では，図3に示すように，水溶液中で帯電している金ナノ粒子をそれと同等のギャップを持つ電極で補足したときの電流応答[1]を電気回路に模して説明した[9]．そこでは，ナノ粒子が電極に捕捉されるときに急激な電流の立ち上がりと減衰が見られることから，粒子が電流経路を形成するスイッチの役割を担うものと考えている（図3(c)）．電極のギャップが導通する瞬間に，粒子の持つ電荷も電流に寄与し電流値の増加が見られる．初期の電流に比べて粒子を捕捉した後の定常電流に若干の増加が見られることから，電極に捕捉された粒子が抵抗の低減に寄与していることを説明し，実験結果[1]との対応を議論した（図2(d)）[9]．


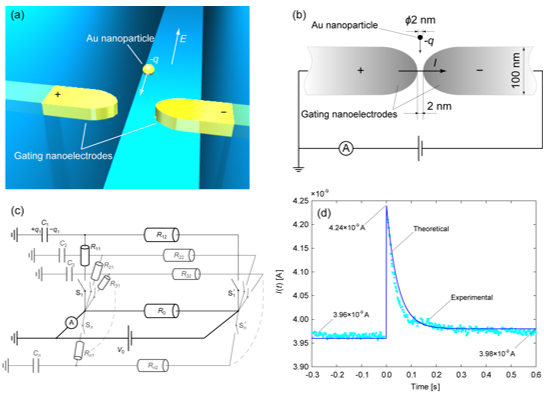
Fig. 3. Schematic illustrations of (a) nano-gapped gating electrodes in a nanofluidic channel to detect a single nanoparticle by tunnel current, (b) dimensions of the experimental system, and (c) electric circuit model of the single particle detection and (d) comparison between theoretical [9] and experimental [1] results.

 

１．３．トンネル電流による単一分子識別

　さらに，トンネル電流による一分子の識別技術に関しても，理論的予測[14]と実験結果[2],[3]から確立されつつある．たとえばDNAを構成する4種類の塩基分子（グアニン，アデニン，チミン，シトシン）の識別が確認され[2]，数10塩基からなる鎖状分子の解読が実現している[3]．我々は，実験における電流値の変化が，各分子の特徴を反映した量子力学効果に基づくトンネル電流によるものであることを説明するために，Heisenbergの不確定性原理から定性的な説明を試みた[10]．ここでは，その理論背景について簡単に紹介する．不確定性原理がΔEΔt≥h/(4π)の形で与えられるとき，エネルギーEと時間tの関係はプランク定数hを4πで割った程度以上に正確には決定できないことを示している．これに対して，Δtの間に系の電荷量QがΔQだけ変化するものとして電流I=ΔQ/Δtを定義すると，上記の不確定性原理から

(1)

を得る．さらに，電気的中性である系に電場が印加されるとき，エネルギーの変化に対して双極子の影響が支配的である場合にはΔE=−ΔD·ΔEextで近似できる．ここで，ΔDは，外部電場ΔEextを印加することで生じる双極子モーメントの変化である．また，素電荷eの変化量ΔNからΔQ=eΔNとし，電荷移動の理論[10]から

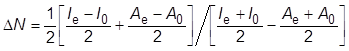(2)

と書ける．ここで，IeとI0はそれぞれ電場存在下と基底状態でのイオン化エネルギーであり，AeとA0はそれぞれ両者の電気親和力である．以上より，ΔD, Ie, I0, AeおよびA0を知ることができれば，式(1)より量子力学効果に起因する電流の程度を見積もることができる．我々は，量子化学計算を用いて上記の物理量を導出することにより各分子固有の電子状態を加味し，DNAを構成するグアニン，アデニン，チミンおよびシトシンについて電流電圧特性を評価した．その結果，伝導性の序列はアデニン＞グアニン＞チミン，シトシンとなり，プリン塩基（アデニン，グアニン）のほうがピリミジン塩基（チミン，シトシン）よりも高い伝導性を示すことが分かった[10]．本結果は，先行研究の実験結果[2]や別法を用いたトンネル電流の理論解析[14]とも定性的に一致した．

 

２．おわりに

　本稿では，電解質溶液中で電気泳動する分子やナノ粒子に対して，イオン電流とトンネル電流によりそれらを検出および識別する手法について紹介した．流体中における一分子の電気計測に関する研究開発は，多方面の研究者が注目している課題であり，今後のさらなる進展が期待される．その中でも，我々は液相における分子流体力学の立場で理論と実験の両面から学術的深化を目指している．

 

謝辞

　 本研究を遂行するにあたり，大阪大学産業科学研究所の谷口正輝教授および筒井真楠准教授にご助力を賜りましたこと，記して感謝の意を表します．

 

参考文献

[1] Tsutsui, M., Taniguchi, M., and Kawai, T., “Transverse Field Effects on DNA-Sized Particle Dynamics”, Nano Letters, Vol. 9, No. 4 (2009), pp. 1659–1662.
[2] Tsutsui, M., Taniguchi, M., Yokota, K., and Kawai, T., “Identifying Single Nucleotides by Tunnelling Current”, Nat. Nanotechnol., Vol. 5 (2010), pp. 286–290.
[3] Ohshiro, T., Matsubara, K., Tsutsui, M., Furuhashi, M., Taniguchi, M., and Kawai, T., “Single-Molecule Electrical Random Resequencing of DNA and RNA”, Sci. Rep. 2, 501 (2012).
[4] Uehara, S., Shintaku, H., and Kawano, S., “Electrokinetic Flow Dynamics of Weakly Aggregated λDNA Confined in Nanochannels”, Trans. ASME., J. Fluids Eng., Vol. 133 (2011), pp. 121203 (8 pages).
[5] Yasui, T., Rahong, S., Motoyama, K., Yanagida, T., Wu, Q., Kaji, N., Kanai, M., Doi, K., Nagashima, K., Tokeshi, M., Taniguchi, M., Kawano, S., Kawai, T., and Baba, Y., “DNA Manipulation and Separation in Sublithographic-Scale Nanowire Array”, ACS Nano, Vol. 7, No. 4 (2013), pp. 3029–3035.
[6] Nagahiro, S., Kawano, S., and Kotera, H., “Separation of Long DNA Chains Using a Nonuniform Electric Field: A Numerical Study”, Phys. Rev. E, Vol. 75 (2007), pp. 011902 (5 pages).
[7] Doi, K., Haga, T., Shintaku, H., and Kawano, S., “Development of Coarse-Graining DNA Models for Single-Nucleotide Resolution Analysis”, Phil. Trans. R. Soc. A, Vol. 368 (2010), pp. 2615–2628.
[8] Qian, W., Doi, K., Uehara, S., Morita, K., and Kawano, S., “Theoretical Study of the Transpore Velocity Control of Single-Stranded DNA”, Int. J. Mol. Sci., Vol. 15 (2014), pp. 13817–13832.
[9]) Doi, K., Ueda, M., and Kawano, S., “Theoretical Model of Nanoparticle Detection Mechanism in Microchannel with Gating Probe Electrodes”, J. Comput. Sci. Technol., Vol. 5, No. 2 (2011), pp. 78–88.
[10] Szarek, P., Suwannawong, S., Doi, K., and Kawano, S., “Theoretical Study on Physicochemical Aspects of a Single Molecular Junction: Application to the Bases of ssDNA”, J. Phys. Chem. C, Vol. 117 (2013), pp.10809–10817.
[11] Kawaguchi, C., Noda, T., Tsutsui, M., Taniguchi, M., Kawano, S., and Kawai, T., “Electrical Detection of Single Pollen Allergen Particles Using Electrode-Embedded Microchannels”, J. Phys.: Condens. Matter, Vol. 24 (2012), pp. 164202 (6 pages).
[12] Uehara, S., Tsutsui, M., Doi, K., Taniguchi, M., Kawano, S., and Kawai, T., “Fluid Dynamics and Electrical Detection of λDNA in Electrode-Embedded Nanochannels”, J. Boimech. Sci. Eng., Vol. 8, No. 3 (2013), pp. 244–256.
[13] Doi, K., Tsutsui, M., Ohshiro, T., Chien, C.-C., Zwolak, M., Taniguchi, M., Kawai, T., Kawano, S., and Di Ventra, M., “Nonequilibrium Ionic Response of Biased Mechanically Controllable Break Junction (MCBJ) Electrodes”, J. Phys. Chem. C, Vol. 118 (2014), pp. 3758–3765.
[14] Lagerqvist, J., Zwolak, M., and Di Ventra, M., “Fast DNA Sequencing via Transverse Electronic Transport”, Nano Lett., Vol. 6, No. 4 (2006), pp. 779–782.
リンク一覧へ戻る
更新日：2014.12.15

↑