流れ　2019年3月号　目次

―　特集テーマ：流体工学部門講演会　― 巻頭言 （橋本，松田，朴） 民間単独での観測ロケット開発と打上げとその後の超小型衛星打上げロケット開発状況 稲川 貴大（インターステラテクノロジズ株式会社） 一様吹出し制御による翼面摩擦抵抗低減効果の実験的定量評価 江藤 薫子，近藤 佑亮，深潟 康二（慶應義塾大学），徳川 直子（宇宙航空研究開発機構） 受動吹出し制御による翼面摩擦抵抗低減の風洞実験 廣川 詩歩，江藤 薫子，近藤 佑亮，深潟 康二（慶應義塾大学），徳川 直子（宇宙航空研究開発機構） 翼に渦が干渉する場合の翼周りの流れと発生する空力騒音に関する研究 小林 典彰（東京大学） 遷音速多段軸流圧縮機における静翼列流れのLES解析 齋藤 誠志朗（九州大学） WALEモデルを用いた円管内乱流のLESにおける格子解像度の影響 岩佐 大器，難波江 佑介，深潟 康二（慶應義塾大学） 流れの夢コンテストに参加して 寺田 智美（北海道大学）   水面制御装置を用いたゴミの分別 本間 俊貴（明星大学） 　｜　リンク一覧にもどる　｜

 

一様吹出し制御による翼面摩擦抵抗低減効果の実験的定量評価

江藤 薫子 慶應義塾大学	近藤 佑亮 慶應義塾大学	深潟 康二 慶應義塾大学	徳川 直子 宇宙航空研究開発機構

1.　はじめに

　第96期流体工学部門講演会において発表⁽¹⁾を行い，日本機械学会若手優秀講演フェロー賞をいただきました．さらにニュースレターとして講演内容を紹介する機会を頂きました．この場を借りて流体工学部門の皆様に御礼申し上げます．本ニュースレターでは，講演内容である，外部からの空気供給を用いた，能動的な一様吹出し制御による翼面摩擦抵抗低減効果の実験的定量評価について紹介させていただきます．なお，本研究の後継テーマである，受動的な一様吹出し制御に関しては，本ニュースレターの別記事⁽²⁾ をご覧ください．

2.　流体摩擦抵抗低減のための一様吹出し制御とその実験的評価手法

　近年，航空機の高エネルギー効率化を目指して，航空機に生じる流体抵抗，中でも全抵抗の約50%を占める摩擦抵抗⁽³⁾ を低減する手法が注目されている．この摩擦抵抗を低減する手法の一つとして，境界層に対して壁面から微小な速度で流体を一様に吹き出す，一様吹出し（UB）制御が挙げられる．Park & Choi⁽⁴⁾ は乱流境界層におけるスリットからの吹出しの効果を直接数値シミュレーション（DNS）によって調査し，局所的に摩擦抵抗が減少することを報告した．Kametani & Fukagata⁽⁵⁾ は空間発達乱流境界層に対しDNS を行い，UB制御による摩擦抵抗低減を確認し，そのメカニズムを報告した．Kondo & Fukagata⁽⁶⁾ は，制御の実用化を視野に入れ，圧力こう配を誘起させた平板上の乱流境界層に対してレイノルズ平均ナビエ・ストークス・シミュレーション（RANS）を行い，圧力こう配を伴う流れ場においてもUB 制御によって摩擦抵抗が低減されるという傾向が変わらないことを報告した．しかしこれらの先行研究は平板上の境界層に対して実施されたものがほとんどであり，翼などの実用的な物体表面上での調査は十分に行われていない．したがって，本研究ではこの制御の実用化を視野に入れ，翼面にUB制御を適用し，その制御効果を風洞実験によって調査することとした．

　制御効果の評価にあたり，翼面上の流体摩擦抵抗の変化を定量的に評価する必要があるが，圧力こう配や翼面からの流体の吹出しが存在する中で直接摩擦抵抗を測定することは困難である．また一般的にも実験で取得できる物理量は限られており，その中で現象を定量的に評価することが実験的研究の一つの課題に挙げられる．本研究では熱線流速計による速度計測を実施しているが，この限られた情報の中でどのように定量評価を実施するのか，また圧力こう配や翼面からの吹出しの影響をどのように捉えるのかという点は，制御効果を評価する上で非常に重要である．したがって，制御による流れ場の変化の調査に加え，その評価方法に関しても十分吟味する必要があると言える．

　以上を踏まえ，本研究の目的を，翼に対して一様吹出し制御を行い，その制御効果を風洞実験によって調査するとともに，その摩擦抵抗低減効果の実験的な定量評価法を検討することとした．

3.　実験手法

　本研究ではJAXA航空技術部門所有の0.65 m × 0.55 m小型低乱風洞を用いた．テストセクションと計測の概要をFig. 1に示す．本研究では局所的な摩擦抵抗低減効果の調査のため，翼上面の境界層速度分布を熱線流速計を用いて計測した．熱線流速計はトラバース装置によって制御されており，主流方向 (x方向) 及び鉛直方向 (z方向) に移動することができる．主流速度はピトー管，テストセクション内温度は熱電対により計測した．翼型にはClark-Y翼を用いており，コード長c = 400 mm，スパン長は2b = 548 mmである．乱流遷移を促すため，翼前縁上面にサンドペーパーを設置した．流体を翼面から吹き出すための装置としては，翼内部にチャンバが設けられており，そのチャンバには透過性のある多孔質蓋が備わっている．本研究ではコンプレッサからチャンバへ空気を送り込むことによりUB制御を実現した．なお吹出し領域は翼の後半上面に設置されている．またy/b = 0 および 0.64の翼断面上には圧力計測用の静圧孔が計35点設置されている．

　試験条件としては，迎角をα = 0°に設定し，コード長に基づくレイノルズ数および一様吹出し制御の強さはRe_c = 1.5 × 10⁶ および主流速度の0.14%，あるいは Re_c = 0.65 × 10⁶および主流速度の 0.31%と設定した．

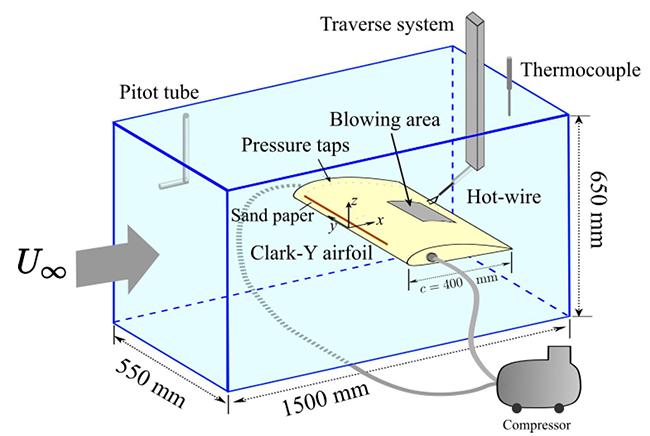
Fig. 1: Schematic of the test section.

 

4.　 実験結果および壁面摩擦抵抗の定量評価法

　計測した翼面上の境界層平均速度分布をFig. 2に示す．この図から，平均速度分布が制御を加えることによって翼面から離れる方向にシフトアップしていることがわかる．これは翼面近傍の速度こう配，つまり壁面せん断応力が低減されていることを示唆しており，UBによって摩擦抵抗が低減されていることを定性的に確認した．

　続いて制御効果の定量評価に取り組んだ．一般的な定量評価法にはプレストン管等を用いて直接摩擦抵抗を計測する方法や，カルマン積分方程式を用いる方法が挙げられるが，前者は逆圧力こう配および翼面からの吹出しの影響，後者は主流方向の計測点の不足から適用困難であった．そこで，局所での境界層速度分布から局所壁面摩擦係数c_fを求めることのできる手法を調査し，修正クラウザー線図法(MCCM)⁽⁷⁾ と，圧力こう配とUBの影響を考慮に入れた壁法則を用いた定量評価法(WL)の二つを導入した．修正クラウザー線図法は，一般的に知られたクラウザー線図法に，圧力こう配の影響による対数則の傾きの変化を加味した手法である．この修正クラウザー線図への平均速度分布のフィッティングを繰り返すことによりc_fを取得した．ただし，この手法は壁面からの吹出しの影響は加味していないため，非制御時の結果への適用に留まる．壁法則を用いた定量評価法でも，平均速度分布を理論分布にフィッティングさせるという手法をとった．ただし，翼面からの吹出しの影響を加味するため，制御時の平均速度には修正Stevenson則⁽⁸⁾ を適用し，吹出しによって変形する速度分布を対数則領域で補正した．また理論分布にはNickels⁽⁹⁾ による圧力こう配を加味した壁法則を採用し，対数則領域において平均速度分布を理論分布へフィッティングさせ，制御時および非制御時のc_fを算出した．以上のフィッティングの様子をFig. 3に示す．

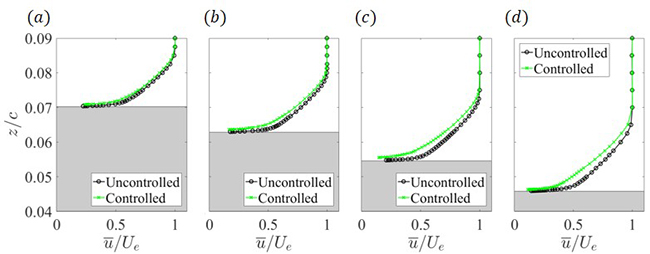
Fig. 2: Mean velocity profiles in the control region
(α = 0°, Rec= 0.65 × 106): (a) x/c = 0.65; (b) x/c = 0.70; (c) x/c = 0.75;
(a) x/c = 0.80.

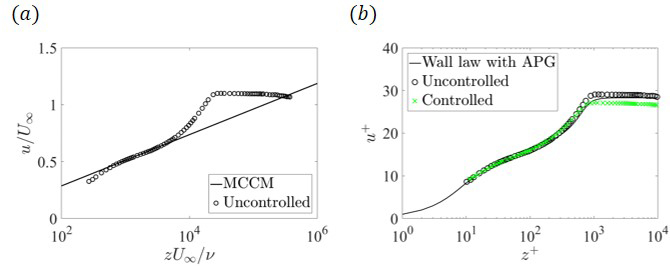
Fig. 3: Sample results of the velocity fitting in the quantitative assessment
(α = 0°, Re_c= 1.5 × 10⁶, x/c = 0.70):
(a) Modified Clauser chart method⁽⁷⁾;
(b) Quantification using the wall law with pressure gradient⁽⁹⁾.

　以上の評価法より得られたc_fの分布をFig. 4に示す．まず，黒の〇および＋で示される各評価法により得られた非制御時のc_fが互いに良好に一致していることがわかる．全ケースを通じてこの差は6%未満であり，各評価法の妥当性を相互に確認した．また，制御を加えることにより，制御領域以降においてc_fが効果的に低減されていることがわかる．得られた壁面摩擦係数を基に局所の摩擦抵抗低減率を算出したところ，21%-66%の低減率が得られた．以上の検討により，翼に対してもUB制御は効果的な乱流摩擦抵抗低減手法であることが示された．

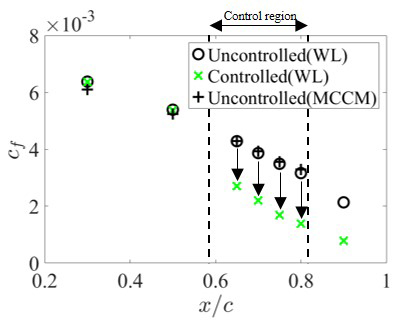
Fig. 4: Skin friction coefficients c_f as a function of streamwise coordinate x.

5.　おわりに

　本研究では翼に対して一様吹出し制御を加え，その摩擦抵抗低減効果を風洞実験によって調査するとともに，その定量評価法について検討した．まず，翼面の境界層速度分布計測を実施し，その形状の変化から定性的に摩擦抵抗が低減されていることを確認した．続いて制御効果の定量評価に取り組んだ．本研究では，壁面摩擦抵抗の定量評価に必要な翼面の物理量が直接測定できないという制約があったため，翼面の平均速度分布を用いた修正クラウザー線図法と壁法則を用いた速度フィッティング法の二つを用いて定量評価に取り組んだ．この結果，それぞれの定量評価法から得られた結果が良好に一致し，双方が妥当な評価法であることを確認した．また21%-66%の局所摩擦抵抗低減率が得られ，一様吹出し制御は翼に対しても有用な摩擦抵抗低減手法であることを定量的に示した．

謝　　　辞

　本研究はJAXA-慶應義塾共同研究「境界層制御による航空機の抵抗低減に関する研究」の一環として実施されました．またJSPS科研費JP16K06900の助成を受けたものです．末筆ながら，選考委員の皆さま，そして今回ニュースレターにて執筆の機会を与えてくださった流体工学部門の皆さまに感謝申し上げます．

文　　　献

(1)	江藤 薫子，近藤 佑亮，深潟 康二，徳川 直子，「一様吹出し制御による翼面摩擦抵抗低減効果の実験的定量評価」，日本機械学会第96期流体工学部門講演会，室蘭，2018年11月29日-30日，Paper OS1-15 (2018).
(2)	廣川 詩歩，江藤 薫子，近藤 佑亮，深潟 康二，徳川 直子，「受動吹出し制御による翼面摩擦抵抗低減の風洞実験」，日本機械学会流体工学部門ニュースレター「流れ」，2019年3月号，Article No. 4 (2019).
(3)	Abbas, A., De Vicente, J., and Valero, E., “Aerodynamic technologies to improve aircraft performance,” Aerospace Science and Technology, Vol. 28, pp. 100–132 (2013).
(4)	Park, J., and Choi, H., “Effects of uniform blowing or suction from a spanwise slot on a turbulent boundary layer flow,” Physics of Fluids, Vol. 11, pp. 3095–3105 (1999).
(5)	Kametani, Y., and Fukagata, K., “Direct numerical simulation of spatially developing turbulent boundary layers with uniform blowing or suction,” Journal of Fluid Mechanics, Vol. 681, pp. 154–172 (2011).
(6)	Kondo, Y., and Fukagata, K., “Friction drag reduction of a spatially developing boundary layer with pressure gradient by uniform blowing and suction,” 11th European Fluid Mechanics Conference, Seville, Spain, Sept. 12-16, 2016 (2016).
(7)	Dixit, S. A., and Ramesh, O. N., “Determination of skin friction in strong pressure-gradient equilibrium and near-equilibrium turbulent boundary layers,” Experiments in Fluids, Vol. 47, pp. 1045–1058 (2009).
(8)	Vigdorovich, I., “A law of the wall for turbulent boundary layers with suction: Stevenson’s formula revisited,” Physics of Fluids, Vol. 28, 085102 (2016).
(9)	Nickels, T. B., “Inner scaling for wall-bounded flows subject to large pressure gradients,” Journal of Fluid Mechanics, Vol. 521, pp. 217–239 (2004).