流れ 2002年11月号 目次
― 特集１．生体内の流れ ―
― 特集２．スポーツと流れ ―
３．部門同好会報告 ｜ リンク一覧にもどる ｜ |
リアリステイク血管モデルにおける流れ
慶應義塾大学理工学部システムデザイン工学科 谷下 一夫
１．はじめに
血液循環系の流れの研究に関して，動脈硬化症の流体力学的発症プロセスを明らかにするために，60年代末に血行力学説が提唱され，動脈内流れの研究が本格的に始まった．その後，多くの研究が行われて来たが，所が，当時では動脈の形態を実際の動脈の病理標本から取り出して再構築するとか，動脈の形態の特徴的なパラメータのみを捕らえた平均的な血管形態の理想モデル内での流れを実験的及び数値的に明らかにした研究が中心であったため，実際の血管病変の発症プロセスを血流と明確に関連付けるには無理があった．そのため現在でも血管病変の流体力学的要因は必ずしも明らかになっていない．そこで，実際の血管形態を忠実に再現して，特定な血管病変内の流れを明らかにするリアリステイクアプローチが必要となった．幸いな事に核磁気共鳴画像（MRI）やX線CTなど非侵襲的に体内の血管形態を忠実に捉える手法が開発されており，捉えられた画像から3次元形態を取り込む事が可能で，そのような3次元形態を基にした流体力学的な研究が展開されている．そのような実際の血管病変に基づくリアリステイクモデルによる研究を予見的研究[prospective study]と称し，実際の診断治療と深く関わって展開されている[1]．そこで，本稿では動脈内流れの予見的な研究の展開について，巨視的及び微視的な視点からの幾つかの具体例を紹介する．
２．巨視的な動脈内流れの研究
動脈内流れで血管病変が顕著に現れる部位は，心臓の冠状動脈，大動脈弓，頚動脈，腎動脈，脳動脈などであり，それぞれの部位での血管病変は心筋梗塞や脳梗塞，或いは動脈瘤などの深刻な疾病の原因となり，臨床サイドからの関心が高い部位である．大動脈弓は曲率の大きい曲り管であり，曲りのある典型的な部位として古くから生理流体力学の分野で注目されていた．曲率が特に大きいため，遠心力による二次流れが著しく加速される流れである．さらに大動脈では心臓の大動脈弁が開いた時のみ血液が流入し，閉じている時は停止するという間欠的な流れである[2][3]．一方，生体内の大動脈弓内の流れをKilner
et al.[4]がMRIを使って初めて可視化することに成功した．彼らの結果によると大動脈の曲りによって回転する渦が形成され，生体内の二次流れの可視化に成功した訳である（図1）．しかしながらMRIの空間分解能は数mmであり，3次元の流れや渦構造を精密に測定するには空間分解能が不足している．とは言え，MRIによって直接血管内の流れを測定できる事は画期的で，彼らのグループはその後心臓内の流れも直接測定し，大きな反響をよんでいる[5]．
脳動脈瘤は発症してある程度増大した後，破裂することはまれで，その割合は，くも膜下出血の既往がなく瘤の最大径が10mm以下の場合でわずか0.05％，10mm以上の場合でも1％程度である[6]．脳動脈瘤の破裂に血流がどのように影響しているかを調べるためには，より詳細な流れの構造を知る必要があると考えられる．そこで，筆者らは脳動脈瘤のリアリスティックモデルを構築し，瘤内の流れ場を詳細に測定して，破裂の可能性を瘤内の流れから予測する可能性について検討した[7]．脳動脈瘤患者のCT連続断層像を体軸方向に重ね合わせ，血管壁のみを抽出し，補間をかけることにより3次元形状データを作成した（図２）．そしてそのデータを用いて光造形法によりエポキシ樹脂のモデルを作製し，キャスティングを繰り返すことにより，アクリルによるモデル流路を作成し，ＰＩＶによって速度ベクトル場を取得した（図３）．モデル流路で得られた速度ベクトルのデータから，破裂した症例と未破裂の症例とでは，流れの構造に明らかな相違が見られる．ただこの流れの違いが直接破裂の原因とするには，まだ生体側の情報が不足しているが，このような研究の積み重ねから，明確な相関が得られると期待される．
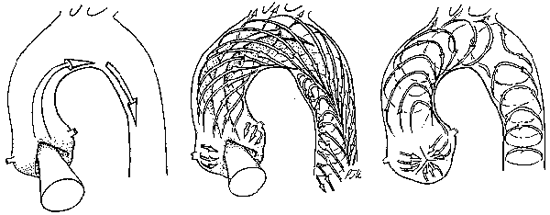
図１：MRIによって観測された大動脈弓の渦
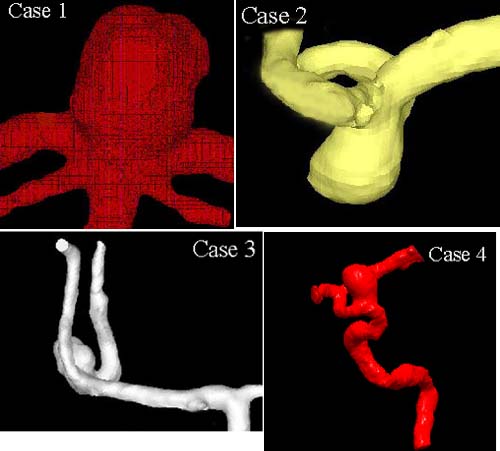
図2：脳動脈瘤の症例．症例３が破裂した例で，その他は未破裂．Case
1：脳底動脈先端部動脈瘤，
case2, 3:中大脳動脈分岐部動脈瘤，case4:内頚動脈眼動脈分岐部動脈瘤
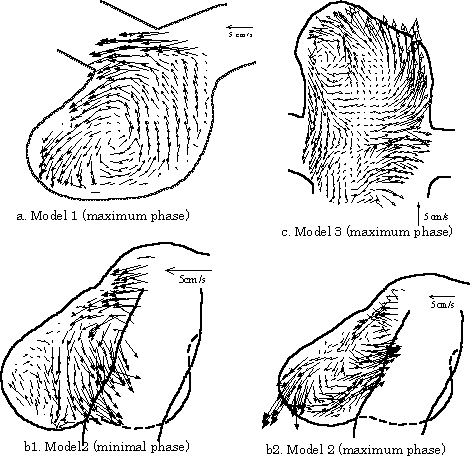
図3：脳動脈瘤内の流速ベクトル図
３．細胞近傍の微視的な流れ
内皮細胞は血管内面を覆う細胞であり，血流の方向が一定の部位では内皮細胞は長円形でその長軸が血流方向に配列しているが，血流の方向が変化する部位や停滞する部位では類円形で方向性はない．細胞スケールの微視的流れ場の解析結果は，流れ負荷による形態変化が力学的環境に対する一種の適応反応であるとことを示唆している．適応機構を明らかにするためには，類円形の細胞が最終的に伸張・配向するまでの形態再構築過程で細胞表面のせん断応力分布がどのように変化するかを把握する必要がある．
実際の細胞スケールでの流れ場の測定はサブミクロンの空間分解能が必要となり，実現困難であるため，１００倍モデルによって流れ場を測定する事とした．即ち，共焦点レーザ顕微鏡によって細胞形状を測定し，光造形法によって作成された100倍拡大モデル近傍の流れを顕微鏡下でＰＴＶによって流速分布を求め，壁せん断応力を定量的に決定する事が出来た．（図４）に静置培養した細胞と24時間流れを負荷した細胞の等高線図を示す[8][9]．等高線間隔は0．3μmである．同時に図４には個々の細胞表面の壁面せん断応力分布を示す．流れを負荷させることによって，流れの方向に伸長しせん断応力分布が低下している．さらに重要な点は，刺激は細胞ごとに異なっていることを示しており，細胞の力学的刺激受容機構を解明するには個々の細胞ごとの考察が必要である．さらに，異なった刺激を受容した細胞間相互の情報伝達もあわせて検討する必要があると考えられる．（図５）に数値計算の結果も示す．
内皮細胞にせん断応力や歪などの物理的な刺激が加わった際に生ずる生物学的応答は様々で，多くの現象が見つけられおり，力学的刺激受容機構を明らかにする事の重要性が多くの学者から指摘されている．そこで，細胞毎の力学的刺激の定量的な評価がますます重要となってくる．従って，細胞生物学の分野においても流体力学的な視点が必要とされており，今後分子生物学的な側面との対応などでますます微視的な流体力学的なアプローチが重要な役割を演じることになるであろう．
図4：実験的に求めた内皮細胞表面のせん断応力分布．上が力の負荷を与えていない場合で，下が与えた場合．
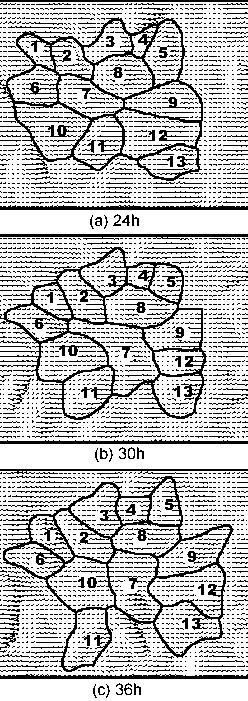細胞表面のせん断応力のベクトル図
(a) ２４時間後
(b) ３０時間後
(c) ３６時間後
図5：数値計算によって得られた内皮細胞群におけるせん断応力の分布
参考文献
[1]Steinman, D.A., Image-based CFD modeling
in realistic arterial geometries, Annals of Biomedical Engineering,
[2002] [to appear]
[2]Naruse, T. and Tanishita, K., Large curvature effect
on pulsatile entrance flow in a curved tube, Trans. ASME,
J. Biomech. Eng.,118 [1996]180
[3]Komai, Y., and Tanishita, K., Fullu developed intermittent
flow in a curved tube, J. Fluid Mech., 347 [1997]pp263-287.
[4]Kilner, P.J., Yang, G.Z., Mohiaddin, R.H., Firmin, D.N.,
and Longmore, D.B., Helical and retrograde secondary flow
patterns in the aortic arch studied by three-directional
magnetic resonance velocity mapping., Circ., 88 [1993] pp.2235-22247
[5]Kilner, P.J., et al. Nature, (2000)
[6]The international study of unruptured intracranial aneurysms
investigators, Unruptured Intracranial Aneurysms - Risk
of Rupture and Risks of Surgical Intervention: N Engl J
Medicine 339 [1998] 1725-1733-
[7] S. Tateshima, Y. Murayama, J.B. Villablanca, T. Morino,
I. Takahashi, T. Yamauchi, K.Tanishita, F. Vinuela, Intra-aneurysmal
flow dynamics study using an acrylic anerysm model manufactured
from CT angiogram, Neurosurgery, Vol. 95, [2001] pp.1020-1027.
[8]Fukushima, S., Nagatsu, A., Kaibara, M., Oka, K., Tanishita,
K., Measurement of surface topography of endothelial cell
and wall shear stress distribution on the cell, JSME, Int.
J. C, 44 (2001),pp972-981.
[9]Fukushima, S., Deguchi, T., Kaibara, M., Oka, K., Tanishita,
K., Microscopic velocimetry with a scaled-up model for evaluating
a flow field over cultured endothelial cells, Trans. ASME,
J. Biomech. Eng., 124 (2002)