流れ 2004年8月号 目次
― 特集:流体情報と融合研究 ―
| リンク一覧にもどる | |
計算と実験を融合した新しい流体解析手法
 東北大学流体科学研究所 流体融合研究センター 早瀬敏幸 |
1.はじめに
流体研究のみならず,現代の科学技術を支える研究手法である実験と数値シミュレーションを一体化することにより,従来の研究手法単独では解決が困難だった複雑・多様化した流体問題を解決することが可能となる.本稿では,実現象の数値シミュレーションを特に「数値リアライゼーション」と呼ぶ理由を説明した後,制御工学におけるオブザーバの概念を流体の数値シミュレーションに応用することによって数値リアライゼーションが実現できることを例を示しながら述べる.
2.数値リアライゼーション
最初に,計測と融合した流体シミュレーションの必要性について説明する.図1は,流体の計算機シミュレーションの発展を示したものである.1949年に世界初の電子計算機が開発されて以来,流体解析は常に計算機が解決すべき主要課題であった.計算機の開発当初は,2次元の単純な流れ場が対象であったが,ハードウエア性能の向上と,数値計算手法の発展により,3次元流れ場,複雑な実形状の流れ場の解析へと進み,現在では,1000万次元を超える計算も可能となっている.計算モデルの点からは,実現象のシミュレーションも可能になりつつあるといえる.しかし,実際には計算モデルとは別にバリアがあって,現在のシミュレーション技術の延長線上で実現することは困難である.すなわち,数値シミュレーションを行うためには,初期条件と境界条件(以後,計算条件と呼ぶ)を与える必要があるが,例えば,1003 = 100万次元の問題の場合,与えるべき初期条件の数は100万,境界条件の数は1002 =1万のオーダーとなり,これを実現象に対して正確に与える(例えば境界条件として,計算ステップごとに1万点の計測データを与える)ことは,現実問題として不可能である.
このように,実現象のシミュレーションは本質的な困難を含んでおり,著者らは実現象のシミュレーションを特に「数値リアライゼーション」と呼んで通常の数値シミュレーション(理想条件下の計算)と区別している[1].数値リアライゼーションを実現するため,現実的な測定点(100のオーダー以下)のデータをシミュレーションにフィードバックし,漸近的にシミュレーション結果を実現象に収束させる研究が行われている.これは,制御分野におけるオブザーバの概念を流体解析に応用したものであり,オブザーバを無限次元の非線形システムである流れ場に対して構成する問題と捉えることができる(図2).このような問題に対するオブザーバ設計の一般的理論は現状では存在しないので,個々の流れ場に対する物理的考察により,適切なフィードバック則を決定している.なお,流れのオブザーバは,計測の立場から見ると,センサの無い場所での計測を実現する「仮想計測」と捉えることも出来る[2].
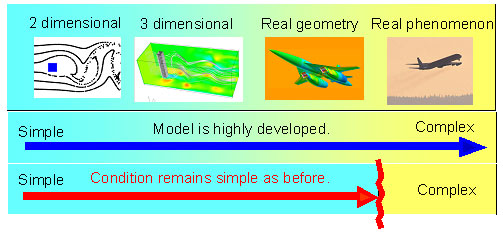
図1 CFDの発展と数値リアライゼーションの必要性
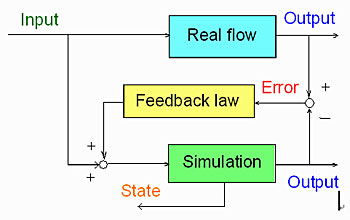
図2 流れのオブザーバのブロック線図
3.数値リアライゼーションの例
流れのオブザーバによる数値リアライゼーションの例を示す.最初に,実際の流れ場を対象とした数値リアライゼーションの例として,ハイブリッド風洞で角柱後流のカルマン渦列を解析した例を図3に示す[3].この例では,風洞実験で角柱の後流に生じるカルマン渦列に対して,数値計算における角柱側面の圧力の誤差を数値計算にフィードバックしている.リアルタイム計算を行うためにかなり粗い格子を用いているため,通常の数値シミュレーションでは,振動数が実験と一致せず,また渦の発生が実験に比べてかなり下流側に移動するなど,流れ場の構造を正確に再現できていないが,数値リアライゼーションでは,カルマン渦による流れの振動の位相も含め,実際の流れ場を正確に再現している.
次に,実際問題への応用例として,医療診断に用いる超音波診断装置とスーパーコンピュータを用いて流れのオブザーバを構成した例を,図4に示す[4].この例は,食道から超音波プローブを挿入し,大動脈に発症した潰瘍周りの血管形状と血流構造を,超音波診断装置により可視化したものである.図(b)は,血流速度の超音波方向成分を可視化表示したもの(カラードプラ)の比較である.通常のシミュレーション[図右上]では,正確な上流境界条件を与えることが困難であり,また,計算モデルも2次元流の仮定などの誤差を含んでいるため,実測結果の複雑な渦構造を再現できていない.これに対して,計測と計算のカラードプラの差を求め,これに比例した仮想的な外力をシミュレーションに加えて計算を行った結果[図左下,右下]では,通常のシミュレーションと同一の境界条件を用いているにもかかわらず,実験で見られる複雑な流れ構造を正確に再現している.
数値リアライゼーションは,本稿で述べた医療応用の他にも,原子力プラントの異常同定,半導体製造のプラズマ流制御など様々な分野への応用が研究されており,複雑なシステムの内部状態をリアルタイムで診断する一般的手法として確立されることが期待される.
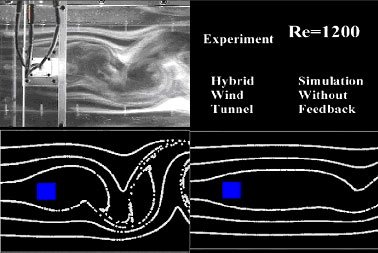
図3 ハイブリッド風洞によるカルマン渦列の解析(クリックすると再生 531KB)
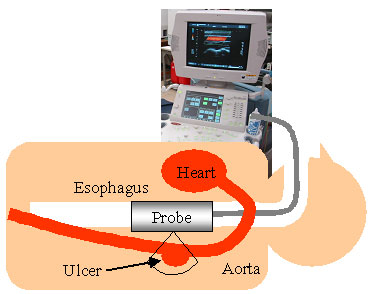
(a) 大動脈の潰瘍
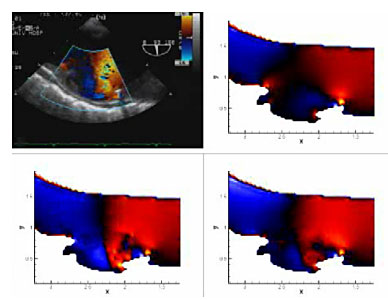
(b) カラードプラ画像(左上),通常のシミュレーション(右上),超音波計測融合シミュレーション(左下,右下)の比較
(クリックすると再生 160KB)
図4 超音波計測融合シミュレーションによる大動脈潰瘍部の血流解析
4.おわりに
以上,本稿では,実験計測と数値シミュレーションを一体化した新しい解析手法について述べた.本手法により,従来の研究手法単独では解決が困難だった,複雑・多様化した流体問題を解決することが可能となるものと期待される.
参考文献
1) T. Hayase, K. Nisugi, and A. Shirai: Numerical Realization of Flow Field by Integrating Computation and Measurement., Proc. Fifth World Congress on Comput. Mechanics (WCCM V), (2002), Paper-ID: 81524, pp. 1-12.
2) 早瀬:流れ場の数値シミュレーションと仮想計測, 計測と制御,Vol. 40, No. 11, (2001), pp. 790-794.
3) K. Nisugi, T. Hayase, and A. Shirai: Fundamental Study of Hybrid Wind Tunnel Integrating Numerical Simulation and Experiment in Analysis of Flow Field, JSME Int. J., Ser. B, Vol. 47, No. 3, (2004).
4) K. Funamoto, T. Hayase, A. Shirai, T. Yambe, and Y. Saijo, Reproduction of Real Blood Flow in Aorta with Ultrasonic-Measurement-Integrated Simulation, Proc. 3rd Int. Sympo. on Advanced Fluid Information, AFI-2003, (2003), pp. 39-40.

