流れ 2006年9月号 目次
― 特集： 風洞・水槽で流れを造る ―
｜ リンク一覧にもどる ｜ |
ACサーボモータでファンを駆動する風洞による風速風向変動の生成
|
|
１．はじめに
風は風速だけでなく風向も変動しながら吹いている．風速と風向がともに変動する気流を生成し，自然風を模擬できる風洞を開発することを目的とする研究を行ってきた．ファンを駆動する AC サーボモータをコンピュータで制御する方式の送風機を斜交配置し， 2 方向の変動気流を合成する方式である．この風洞装置によって風速や風向が非定常に変化するときに物体に作用する空気力の特性を調べた．
２．送風機の諸元
用いた送風機は図１に示すように吹き出し口が口径 10cm の円形断面の小型なものであるが，最高風速 13 m/s ， 0.1 秒で 10 m/s の風速差を達成する能力を有している．
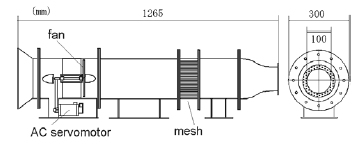
図 1 AC サーボモータでファンを駆動する送風機
３．放射状に配置した送風機による風速・風向変動の生成
図 2 に示すように AC サーボモータ送風機２本を水平面内に斜交配置し， 2 方向の気流を合成させる． 2 本の送風機の狭角は 45 度
とした．予備的な実験によれば， 2 本の送風機から同じ風速
の定風速気流を発生させて合成すると，合成気流の方向は中心軸方向
となる．このとき合成気流の乱れ強さは単独気流の倍程度（およそ 1 ％が 2 ％程度）になるが，脈流のような不正な変動は発生しないことが確認された．
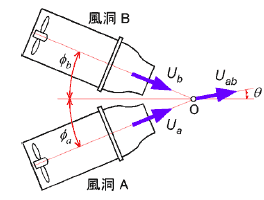
図 2 水平面内に斜交配置した送風機のレイアウト
そこで 2 方向の気流風速
，
を種々組み合わせて，気流合流点［図 2 の点 O ］における合成気流の風向 
と風速 
を測定した．測定結果より，最小二乗法を用いて多項式で表した次の 2 つの関係式の係数
を決定する．
図 3, 4 は求めた式 (1), (2) をグラフ表示したものであり，滑らかな曲面を形成している．この関数から目標とする合成気流の風速 と風向 に対する各送風機の風速変動 と を逆算し，制御電圧の時系列を作成して 2 つの風洞を駆動する [1] ．
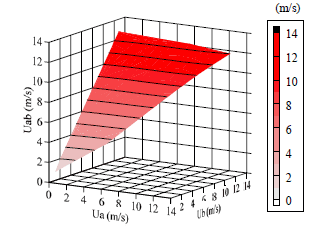
図 3 測定された と , の関係
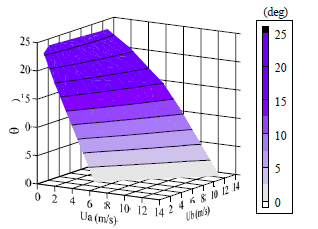
図 4 測定された と , の関係
４．乱流の生成
2 本の送風機の中心軸方向 
風速成分
と中心軸直交方向成分
は次式で定義できる．
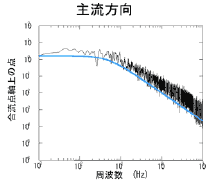
この関係を用いて風速成分 と がともにカルマンスペクトルに従う合成気流を作成した．図 5 は合成気流の変動スペクトルの例である．目標のスペクトル分布に従った気流変動を得ることができている．
 |
 |
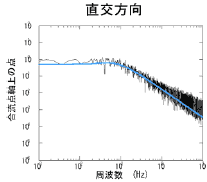図 5 合流点の気流変動（平均風速 
，乱れ強さ
，乱れスケール
）
［左図：主流方向変動（ 成分），右図：直交方向変動（ 成分）］
５．脈動気流下の正方形角柱に作用する空気力の測定
AC サーボモータ送風機が急激な風速変動の気流を生成できることを利用して，風速振幅が大きい脈動気流による空気力の非定常特性を検討する実験を行った [3] ．海洋工学の分野では周期的に流れを反転させ，変動流速の中央値がゼロという条件で多くの研究がなされている．これに対し，本研究では非ゼロの平均風速を持つ脈動流を生成し，正方形角柱に作用する空気力を測定した．図 6 に空気力の定義を示す．辺長 D ＝ 3cm ，軸長 L ＝ 10cm の正方形角柱模型（材質：桂）を 4 枚の板バネ（材質：燐青銅，厚さ 3mm ，ヤング率 E ＝ 1.1×104kgf/mm2 ）で支持し，作用空気力をひずみゲージを用いて測定する．
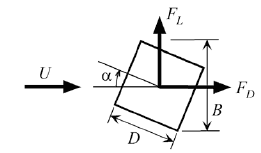
図 6 正方形角柱に作用する空気力の定義
測定空気力（抗力：
，揚力：
）をモリソン公式 ( 風速の二乗に比例する成分
と風速の時間勾配
に比例する成分
を加えた式で表すと，次式のように示せる．
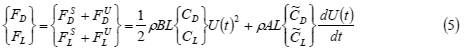
ここで
は空気密度， 
は角柱断面積，
と
は慣性力成分の無次元係数である．
実験結果の一例として，迎角 22.5 °の正方形角柱に，風速の中央値
，片振幅
，周期
の 脈動気流を与えた場合を示す．図 7 は測定した空気力の抗力成分
に関する時系列波形である． なお細かい変動は空気力測定装置の固有振動数 25Hz に対応するものである． 風速の 2 乗
の波形から抗力係数
を評価すると，緑の線で示された波形が得られ，測定値との間に位相の差異が生じる．係数を評価して慣性力成分を加えると，黒の線で示された波形が得られ，測定値の波形に近い波形を得ることができる．図 8 は揚力成分
に関するもので，図 7 と同様に慣性力成分を考慮することによって脈動気流による空気力変動をよりよく評価できる結果になっている．
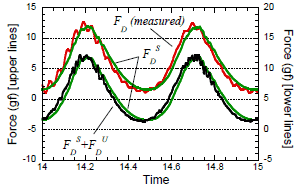
図 7 脈動気流を作用させた正方形角柱の変動抗力
［赤：測定値，緑：
，黒：
］
（見やすくするために 5gf ずらしてプロットしている）
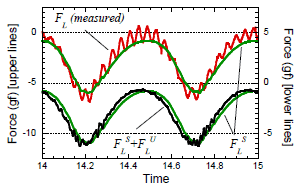
図 8 脈動気流を作用させた正方形角柱の変動揚力
（赤：測定値，緑：
，黒：
）
（見やすくするために 5gf ずらしてプロットしている）
このような測定を迎角
と周期 
を変えて行った結果を表 1 に示す．ここで 
数は
と定義する．
表 1 評価された空気力係数
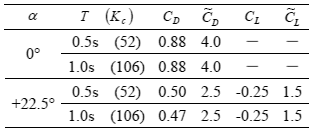
無次元係数 
について， Okajima [5] は
， Blevins [6] は
（付加質量係数
として）という値を示している．本研究の
はこれらの値より大きい値が得られた．
図１の送風機を挟角 45 度で 3 本配置し， 2 本ずつの気流を合成させることにより，図 9 のように± 45 度の範囲で風向を時間変化させることができる装置を作成した．この装置を用いて正方形角柱に作用する空気力に対する風向の時間変化率の影響を測定した [2] ．
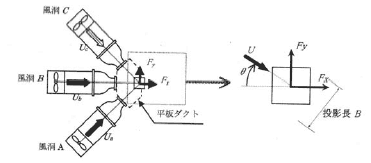
図 9 3 本の送風機による風向が変化する気流の生成と空気力の定義
図 10 は実験に用いた合成気流の一つであり，風速がほぼ一定 (12m/s) で， -45 度から +45 度までの 90 度を 1 秒間で風向が変化する［時間変化理知 
］．他に
の気流を用いた．
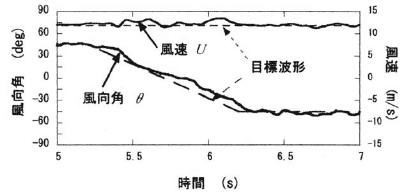
図 10 図 9 の装置で生成させた気流の風速と風向 
図 11 はそれらの気流によって正方形角柱に作用する空気力
の無次元係数
の変化を定常風向の気流による値と比較して示す．また図 12 は空気力係数
の変化である．いずれも，風向変化率が大きくなるほど定常風向による空気力の値との差が大きくなる傾向にある．
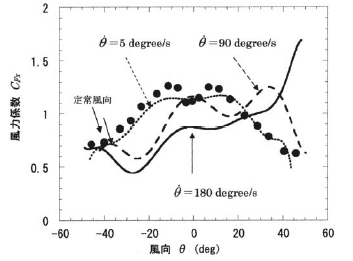
図 11 定常風向気流と風向変動気流の風力係数
の比較
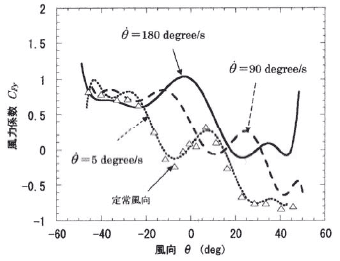
図 12 定常風向気流と風向変動気流の風力係数
の比較
７． おわりに
送風機のファンを AC サーボモータで駆動する送風機を複数組み合わせて， 2 方向の気流を合成する方式で，風速と風向が非定常に変動する合成気流を生成させる風洞装置を作成し，乱流の生成，角柱に作用する非定常空気力の測定などを行ってきた．現在， 4 つの AC サーボモータで 4 つのファンを駆動することにより 40 cm × 40 cm の正方形断面の送風機を用いて本研究の展開を試みている．
参考文献
[1] 野村卓史，山縣大樹，木村吉郎： AC サーボモータでファンを制御する風洞による風速風向変動の生成，第１５回風工学シンポジウム論文集， pp.197-202, 1998.
[2] 野村卓史，関野洋一郎，鈴木洋司：風向が時間変化する気流による非定常空気力の測定，第 17 回風工学シンポジウム論文集， pp.297-302, 2002.
[3] T. Nomura, Y. Suzuki, M. Uemura and N. Kobayashi, Aerodynamic forces on a square cylinder in oscillating flow with mean velocity, Journal of Wind Engineering and Industrial Aerodynamics, Vol.91, pp.199-208, 2003.
[4] 野村卓史： AC サーボモータ送風機による風速風向変動の生成と空気力測定，最新の風洞実験法に関する比較研究，研究集会（一般） 13K-5 ，京都大学防災研究所， pp.49-52,
[5] A. Okajima, T. Matsumoto and S. Kimura, Force measurements and flow visualization of circular and square cylinders in oscillatory flow, Proc. of JSME, B, Vol.63, No.615, pp.58-66, 1997.
[6] R.D. Blevins, Flow-Induced Vibration, 2nd ed., Van Nostrand Reinhold, 1990.