流れ 2009年9月号 目次
― 特集テーマ: 特集テーマ: 界面を含む流れのシミュレーション ―
| リンク一覧にもどる | |
分子シミュレーションで見た微小気泡
松本充弘 |
1.微小気泡の不思議
直径がmmよりも十分に小さい気泡(図1)は,微小気泡あるいはマイクロバブルとよばれて,最近いろいろな方面で注目を集めている(1).ミリメートル級の気泡でも,その表面積比が大きいことを利用した気体の溶解促進や浮遊選鉱など古くから数々の応用例があるが,せん断流などを利用して手軽にマイクロバブルを発生させる機器が登場したことにより,化学反応や医療工学など新たな利用方法が開拓されつつある.
応用技術が先行している微小気泡であるが,いろいろな「謎」が存在する.たとえば
(1) 表面張力のために微小気泡内は非常に高圧になっているはずだが本当か?
(2) 水や水溶液中での微小気泡は多くの場合に帯電していることが実験的に知られているが,その由来は?
(3) 気泡の合体や消滅時には何が起きているのか?
など,基礎的な興味をかき立てられるとともに,その解明が新たな応用につながりそうな魅力的な謎がある.

図1 水中のマイクロバブルの例.
私たちは,分子動力学(MD)法を基礎としたミクロスケールシミュレーションによって,微小気泡のいろいろな基礎的特性の解明に取り組んでいる.ここで,その一端を紹介する.
2.微小気泡の平衡物性を調べる
最初の謎は,平衡状態における半径R の球形気泡について成り立つ,有名なYoung-Laplace式に始まる:
pV=pL+2γ/R (1)
ここでpV は気泡内の蒸気圧,pL+は気泡周囲の液体圧力,γ は表面張力(気液界面張力)である.この式自体は単純な力の釣り合いを記述する式であり,疑う余地はあまりない.ここで,気泡内外の圧力差Δp≡pV-pL+2γ/R に注目する.たとえば大気圧下で室温付近の水(γ≈70×10-3N/m)を考えよう.R=1mmのミリバブルでは,Δp=140 Paで,測定誤差の範囲内である.しかし,R=1µmではΔp=1.4 hPaとなり,気泡内は2気圧以上になる計算である.もしR=10 nmのナノバブルが安定に存在したとすると,何とΔp=140 hPaとなり,気泡内に200気圧以上の気体(例えば空気+飽和水蒸気)がないと気泡を支えることができないはずである.
このように大きな圧力差が予想されるにもかかわらず,なぜ大気圧下でマイクロバブルが存在できるのかについて,いくつかの説明が考えられる.すぐに思いつくのは,表面張力や飽和蒸気圧が曲率依存性をもっているという可能性であろう.たとえば,もしマイクロバブルの表面張力がR に比例して小さくなるならば,Δp は発散しない.実験的な検討は困難であるため,私たちは微小気泡の分子シミュレーションを行ない,その平衡物性を調べた.Lennard-Jonesポテンシャルによるモデル液体の結果を文献(2)に,TIP4Pモデルポテンシャルによる水の結果を文献(3)に報告した.水の結果の一部を図2に示す.予想に反して,いずれの液体でも,表面張力も飽和蒸気圧も気泡半径にはほとんど依存しないことがわかった.

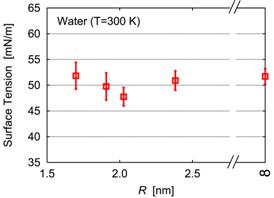
図2 水中の微小気泡の分子シミュレーション例(3).(左)断面図,(右)表面張力のサイズ依存性.シミュレーションに用いたモデルポテンシャルでは,バルクの表面張力は52 mN/m 程度であり,実験値(~71 mN/m)よりやや小さい.
次に考えられるのは,気泡表面に吸着物質が存在することによって表面張力が低下している可能性である.特に,水や水溶液の場合には,気泡が帯電していることが指摘されており(4),イオン吸着は表面張力にも大きな影響を与えていると思われる.しかしながら,電荷の符号や帯電量は水素イオン濃度や塩濃度に大きく依存しており,吸着種や吸着領域の特定はまだ完全には行われていない.さらには,第一原理計算によるイオン吸着解析の結果(5)とも相容れないところがあり,今後の研究が待たれる.
3.微小気泡のダイナミクスを調べる
ミクロスケールの流体のダイナミクスを調べることは,分子シミュレーションの得意とするところである.ここでは,微小気泡に関する計算例を3つ紹介する.
図3 核沸騰最初期過程の分子シミュレーション例(6). ムービーと解析結果.
最初は,加熱面上での微小気泡の発生,すなわち核沸騰の最初期過程のシミュレーションである(6).図3に示すようなセルに液体を入れて底面から一定の熱流束を加えると,気泡核が生成する.加熱条件によっては,熱伝導と蒸発による温度低下のために,数回の気泡振動が観測されるのが興味深い.
次の例は,気泡の合体や破裂時に見られるような液膜の安定性に関する計算例である.ある厚さD をもつ平らな液膜に半径R の穴が開いた状況を考える.この穴が自発的に塞がるか,それとも次第に拡大して膜が破れるかは,表面積の変化を簡単な手計算で求めることで判断でき,定性的には0.5D≤R のような大きな穴の場合に膜の崩壊に至ると予測できる.図4は分子動力学シミュレーションによりその過程を実証した例(7)である.
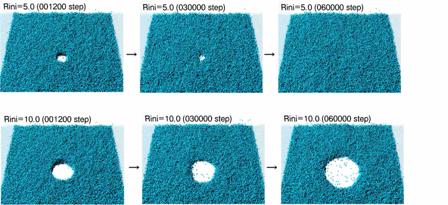
図4 液膜に穴をあけるシミュレーションの例.厚さ10の液膜に半径Rの穴をあけた後の変化(7).
(上段)R=5.0,(下段)R=10.0.長さは分子直径で無次元化している.
実用的な問題へのアプローチを考えると,以上のような分子レベルのシミュレーションには限界がある.私たちは,分子シミュレーションと連続体レベルのCFDシミュレーションのハイブリッドによる気泡ダイナミクス解析の試みを始めているので,その一例を最後に紹介する.これは,激しく変動する気泡表面の近傍や気泡内部はMD法で,比較的ゆっくりと変化する液体部分は従来のCFD法で扱うというアイディアである.MD領域とCFD領域の境界は,両側の圧力差によって移動させる.全領域をMD法で扱う場合にくらべて計算時間を大きく節約できるとともに,CFD法における厄介な移動境界問題が少し単純になり,また,動的表面張力などの入力パラメタを必要としないことが大きな長所である.例として,平面圧力波が通過する際に微小気泡が非球形に崩壊する様子を図5に示す.空間スケールがかなり異なるため,実験やマクロなCFD計算結果との直接比較はまだ行っていないが,変形の様子など定性的には妥当な結果と考えている.表面吸着が存在する場合の崩壊挙動など,このハイブリッドシミュレーションはいろいろな適用範囲が考えられる.
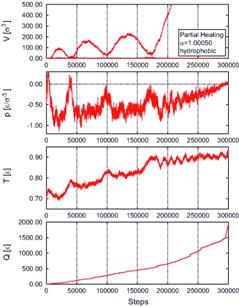
図5 圧力波通過による微小気泡崩壊のMD-CFDハイブリッドシミュレーションのムービー例(8).実線は液相部分の等圧線である.
参考文献