流れ 2009年9月号 目次
― 特集テーマ: 特集テーマ: 界面を含む流れのシミュレーション ―
| リンク一覧にもどる | |
二相系格子ボルツマン法による混相流シミュレーション
稲室 隆二 |
1.はじめに
気液や液液混相流に見られるような界面が複雑に変形する混相流の問題は,機械工学だけでなく様々な理工学分野で重要な研究課題であり,近年,この分野における数値シミュレーションが急速に発展している.界面を含む混相流の数値解析法は移動境界流れ問題と呼ばれ,界面をいかに取り扱うかによって種々の方法が提案されている.これまで,VOF法,Front Tracking法,Level Set法がよく用いられている.これらの方法では,界面を流れとともに自由に変形する(一般には厚みのない不連続な)数学モデルとして取り扱っている.一方,界面を厚みのある連続領域として取り扱う物理モデルである拡散界面モデル(Diffuse Interface Model)1)が最近注目されている.本モデルでは,界面を秩序パラメーターの値によって識別し,界面の変化は自由エネルギーが最小になるように自律的に決まるため,界面のつなぎかえや分裂を問題なく取り扱うことができる.本稿では,格子ボルツマン法(Lattice Boltzmann Method, 以下LBM)2,3)と拡散界面モデルとを組み合わせた二相系LBMを用いた混相流シミュレーション結果について紹介する.なお,紙面の制限から,動画による非定常流れの様子のみを示している.二相系LBMの詳細および計算結果の定量的な整理や実験結果との比較等については参考文献を参照されたい.
2.二相系格子ボルツマン法
LBMの特徴は,①アルゴリズムが簡単であり,また,並列計算に適している,②質量および運動量の保存性に優れている,③衝突項の形を変えるだけで単相流から混相流まで統一的に取り扱うことができる,ことである.混相流シミュレーションにおいては,上記②の特徴が重要である.すなわち,例えば,質量保存性が良くないと,計算を進めて行くに従って液滴や気泡の体積が変化する.それを防ぐために,再初期化などにより体積保存を維持する必要がある.一方,二相系LBMでは体積保存性が良いために,体積保存のための特別の工夫を必要としない.しかし,従来の二相系LBMでは,密度比が約10程度までの計算が可能であるが,それ以上に密度比が大きくなると界面近傍での圧力場の計算が不安定になる.筆者らは,圧力場を安定に計算するためにProjection法を用いて密度比が1000までの計算が可能な二相系LBMを開発した4).その後,大きな密度比に適用できる二相系LBMの開発が盛んであるが,実用計算に適用できる手法はまだ発展途上にある.今後のさらなる発展が期待される.
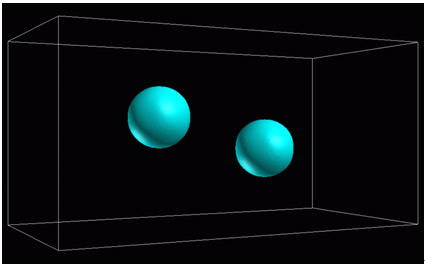
3.液滴衝突
まず,気体中の2つの液滴の衝突シミュレーション結果を図1に示す.気液の密度比=50,Reynolds数=2,000,Weber数=79.5,衝突係数=0.5の結果である.動画よりわかるように,2つの液滴は衝突した後,伸びながら変形し,最終的には2つの大きな液滴と1つの小さな液滴に分裂することがわかる.これは,stretching separationと呼ばれる分裂形態である.このように,衝突時における液滴の複雑な挙動が安定して計算できることがわかる.Weber数と衝突係数との組み合わせを変化させると,coalescenceやreflexive separationと呼ばれる衝突形態が現れる5,6).また,それぞれの液滴内部に異なった色の多数のトレーサー粒子を配置し,その軌跡を逐次計算することにより衝突時の混合状態を計算することができる.
4.気液上昇流
次に,分岐部を上昇する冷媒の気液二相流シミュレーション結果を図2に示す.左図は気液界面を表し,右図は中央断面の気液分布を表している.気液の密度比=45,Reynolds数=12,000とした結果である.下方の入口から流入した気液二相流が上方の2つの出口から流出している.2つの出口から流出する気液二相流のボイド率の差異を求めるのを目的とした計算である.動画よりわかるように,複雑な気液二相流の挙動が長時間にわたって安定に計算できている.図2は分岐部を垂直に置いた場合の計算結果であるが,分岐部を斜めに置いた場合の計算も行い,2つの出口から流出する気液二相流のボイド率の差異を求めている7).
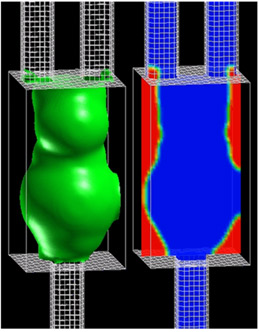
図2 分岐部を流れる気液二相流
(▲図をクリックすると動画を開始)
5.固液混相流
最後に,密度が等しい液液二相流シミュレーション法8)を用いた固液二相流の計算結果を紹介する.上で述べたように,二相系LBMでは,界面の変化は自律的に決まるため,界面の座標を追跡する必要がない.そのため,移動境界問題を容易に取り扱うことができる.以下では,一方の液滴の粘性係数を大きくし,なおかつ,界面張力を大きくすることで「硬い液滴」を作成し,この「硬い液滴」で固体粒子を模擬して固液二相流シミュレーションを行った結果を示す.ただし,「硬い液滴」はそのままでは界面張力のために球形になる.この球形模擬粒子に適当な遠心力や圧縮力などの人工的な体積力を加えることにより,非球形模擬粒子を作製することができる.図3に正方形ダクト内を流れる2つの両凹円盤粒子の挙動シミュレーション結果を示す.左上図が上方から見た図,左下図が側面から見た図,右図が出口から見た図を示している.ダクトの入口および出口には圧力差のある周期境界を用いているので,2列の両凹円盤粒子の挙動を見ていることになる.Reynolds数=104である.動画からわかるように,2つの粒子はダクト中心のまわりを姿勢を変えながら螺旋軌道を描いて周期的な運動をしながら流れる.また,一方の粒子が他方の粒子の姿勢および軌道をちょうど半周期ずれて追いかけることがわかる9).
図3 正方形ダクト内を流れる両凹円盤粒子
(▲図をクリックすると動画を開始)
6.まとめ
二相系LBMを用いた気液および固液混相シミュレーション結果を紹介した.本文でも述べたが,二相系LBMの特徴は各相の体積保存性が良いことである.そのため,図2および図3に示したように,再初期化のような特別な工夫をせずに長時間の計算(例えば,図2の計算では3,000,000ステップ)が可能である.ただし,今後の課題は,(他の大部分の数値解析法も同様であるが)界面の厚さが数メッシュになるため,実際の界面の厚さに比べてかなり大きくなることである.したがって,界面の厚さが重要となる問題には,界面近傍により細かな格子を用いる多重格子による計算などの工夫が必要である.
最後に,多くの研究者や技術者が二相系LBMに興味を持ち,手法の発展とともに応用分野が広がることを期待している.
参考文献