流れ 2011年12月号 目次
― 特集テーマ: 医療と流体工学 ―
| リンク一覧にもどる | |
数値流体シミュレーションを用いた摩擦音"s"発音分析への取り組み
野崎一徳 |
1.はじめに
歯科治療においてマウスピース(図1(a))や義歯(図1(b))のような補綴物の設計は,その着用度合いや予後を左右するため重要である.特に前歯部分の設計では,主に強度,かみ合わせ,そして審美性に重点がおかれている.しかし,設計時に発音時の調音機能への影響は十分考慮されていない.Palmer(1)は,総義歯の設計に際し,前歯の果たす役割として,摩擦音調音を挙げ,その物理メカニズムを推測し,上顎口蓋部と舌との間で作られる隙間から乱流ジェットが生成され発生すると報告している.ただし,具体的研究データが示されていないため,義歯設計に十分な影響を与えられていないと考えられる.そこで,今回,Palmerの推測を基に,摩擦音"s"調音時の口腔内の流れと音源を数値流体シミュレーションによって可視化し,前歯が"s"音の発生に及ぼす影響について考察する.
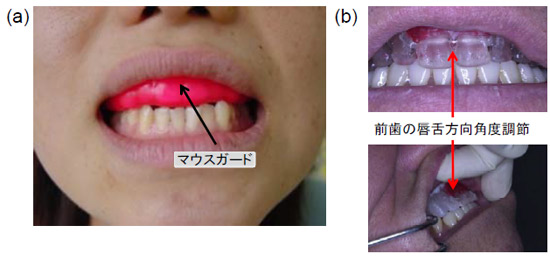
Fig.1. (a)マウスガードを上顎歯列部に装着した様子.(b)上顎前歯の唇舌方向の角度の設定を行い,発音に適した角度を決めている様子.
2.摩擦音"s"とは
図2は顎顔面領域の矢状断面図である.図3(a)は"s"発音時に上顎口蓋部と舌が接触する領域を示している.発音時の気流は青矢印で示したように,左右両側の上顎口蓋部と舌との間で封鎖された隙間を流れる.図3(b)は"s"発音時の核磁気共鳴装置(MRI)による矢状断面図である.このように,左右両側の上顎口蓋部と舌との間で封鎖された隙間をSibilant groove(2)と呼んでいる.
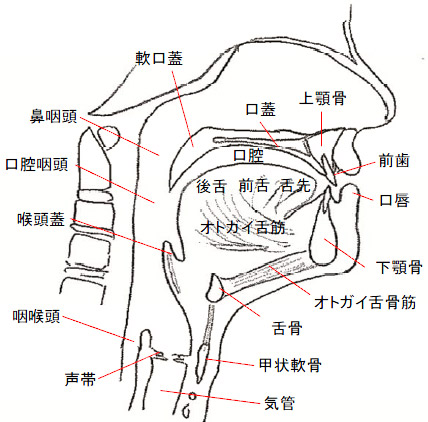
Fig.2. 顎顔面領域の矢状断面.口腔は口蓋,舌,歯列,口唇で囲まれた空間である.
3.摩擦音"s"発音時の数値流体シミュレーション
3.1.摩擦音"s"発音時の口腔内形状の取得
発音時の口腔内形状を計測するには,MRIか,X線断層撮影装置(CT)を用いる.MRIを用いると,被曝がなく何度も撮像でき,さらに時系列で口腔内形状を計測出来る.しかし,歯列については撮像されないため,歯列補間方法が幾つか提案されている.CTは被曝の問題から短時間で限られた回数しか撮像が許されない.しかし,歯列と口腔組織を同時に撮像可能である."s"発音時の口腔形状については,その形状は定常的であり,また,コーンビームCTと呼ばれる歯科用CTを用いれば低被曝で且つ短時間(9.6 s)で0.1 mm立方の解像度のボリュームデータを取得できる.そのため本研究では,大阪大学歯学部倫理委員会の承認を得た上で,実験に同意を得られた被験者1名に対してコーンビームCT(CB MercuRay)にて撮像を行った(図2(a)).
図2(b)は,512 x 512 x 512 pixel で得られた顎顔面領域のボリュームデータから,空気部分を抽出した結果を示している.コーンビームCTは被曝量が少なく高速で高精細に撮像できる一方で,CT値を用いることが出来ず,またノイズが多い欠点がある.そのため,興味領域の抽出のために,異なる2つの閾値を用いた.
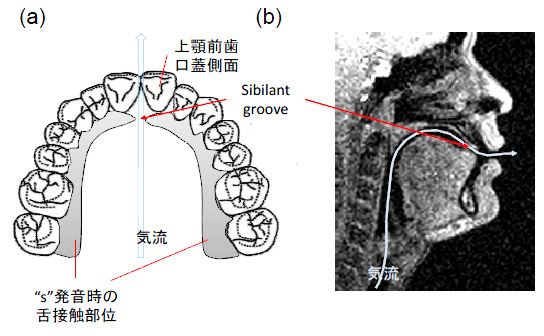
Fig.3. (a)摩擦音"s"発音時の口蓋と舌の接触部分.上顎前歯口蓋側歯茎付近に前舌が接触しない領域があり,この部分をsibilant grooveと呼ぶ.青矢印は気流の通過する方向を示している.(b)"s"発音時の顎顔面領域矢状断面像.MR画像であるため歯列が撮像されていない.前舌が口蓋に押し当てられている様子がわかる.白矢印は気流が通過する方向を示している.
3.2.乱流計算手法
Palmer(1)が言及しているように,Sibilant grooveから乱流ジェットが生じると推測されるため,数値流体シミュレーションにおいて乱流を考慮に入れなければならない.また,乱流から生じる音を推測するためには,乱流中の渦の空間,時間的変化を求める必要がある.本研究では,空間フィルタリングを用いることで計算格子では解像しきれない渦と,直接ナビエ・ストークスの式を解くことで求めることが出来る大きな渦に分け,サブグリッドスケールモデル(SGSモデル)を適用することで小さな渦と大きな渦を分けることによって生じるSGS応力を求めることが出来るLarge Eddy Simulation (LES)を用いた.空間フィルタリング幅は計算格子要素の体積の3乗根とし,口腔のような複雑な形状に適応可能であると考えられるDynamic SGSモデルを用いた.
図4(b)で示したボリュームデータを元にして構築した計算格子を図5(a)に示す.この計算格子は全て6面体で構築されており,マルチブロック構造格子に分類される.壁面付近については法線方向に壁面に垂直な格子を3要素配置した.境界条件については,壁面に滑りなし条件を与え,流出条件として圧力ゼロを与えた.流入境界条件は,人の呼気流量の影響を考慮(3)し,450 mL/sとした.実際の計算にはFrontFlow/Blue v 5.3を用いた.
音源の強さおよび場所を評価する指標としては, Lamb vector divergence φ(4)を評価した.これは,
| φ=∇・(ω×u) | (1) |
として,与えられる.ここで,∇は微分演算子,ωは渦度ベクトル,uは速度ベクトルである.
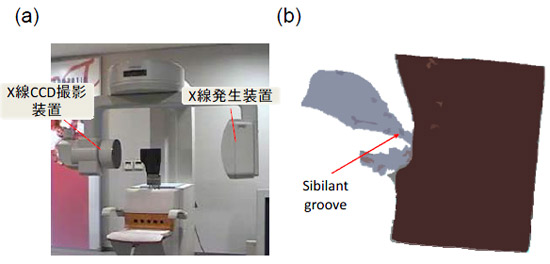
Fig.4. (a)コーンビームCT装置.被験者の座位での口腔内断層像を撮影することが可能.(b)コーンビームCT装置から出力された512 x 512 x512 pixelのボリュームデータから,空気に相当するボクセルを抽出した結果.
4.実験結果
図5(b)は,250本の流線で,色は流れベクトルの絶対値を示している.この結果より,口腔を流れる空気が,Sibilant grooveで速くなり,上下前歯付近を通過する際に流れが大きく乱れ,その舌唇に衝突し,口腔外へ流れ出る様子が分かった.
図6(a-1), (b-1)は,渦管の存在する領域を示しており,(a-1)は,∇2P = 7.0E+08 kg/m3/s,(b-1)は∇2P= 7.0E+09 kg/m3/sの等値面である.この結果から,前歯上流側のsibilant grooveにおいて,すでに渦管が生成されていることが分かった.また,上下前歯付近においても渦管が生成され,舌唇に衝突時には更に多くの渦管が生じていることが分かった.図6(a-2), (b-2)は,(a-1), (b-1)で示した∇2P の等値面に加えて,Lamb vector divergence φ= -1.0E+9, -1.0E+10 1/sの等値面を示している.この図から,∇2P とLamb vector divergence φは異なる物理量にも関わらず,何らかの空間的関係性が有ることが推測された.特に,図6(b-2)では渦管(∇2P = 7.0E+09 kg/m3/s)とLamb vector divergence φ= -1.0E+9 1/s)の等値面の位置関係はほぼ一致していた.図6(a-3), (b-3)は,(a-1), (b-1)で示した∇2P の等値面に加えて,Lamb vector divergence φ= 1.0E+9, 1.0E+10 1/sの等値面を示している.(a-3)では渦管(∇2P = 7.0E+09 kg/m3/s)とLamb vector divergence φ= 1.0E+9 1/s)の等値面の位置関係は近接しているように思われたが,(b-3)では位置関係がずれていることが分かった.
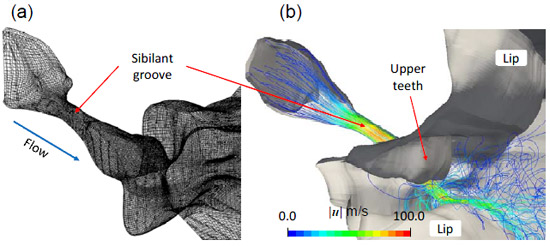
Fig.5. (a)LES解析に用いた6面体計算格子の矢状断Clip画像.青矢印は流入境界条件に与えた流れの方向.(b)LES解析の結果.流線を表示している.色は流れの速度ベクトルの絶対値.
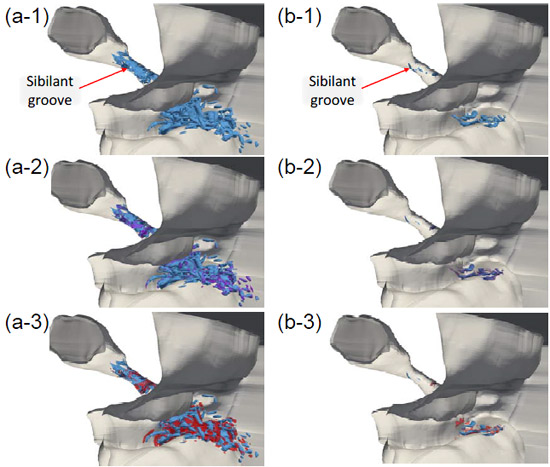
Fig.6. (a-1)渦管(7.0E+08 kg/m3/s), (b-1)渦管(7.0E+09 kg/m3/s), (a-2)渦管(7.0E+08 kg/m3/s)とLamb vector divergence φ (-1.0E+9 1/s)の等値面を重ね合わせた図.青が渦管,紫がφ.(b-2)渦管(7.0E+09 kg/m3/s)とLamb vector divergence φ (-1.0E+10 1/s)の等値面を重ね合わせた図.(a-3)渦管(7.0E+08 kg/m3/s)とLamb vector divergence φ (1.0E+9 1/s)の等値面を重ね合わせた図.(b-3)渦管(7.0E+09 kg/m3/s)とLamb vector divergence φ (1.0E+10 1/s)の等値面を重ね合わせた図.
5.考察
Lamb vector divergence φの等値面の正負による領域の違いは,上顎前歯での剥離による渦管と下顎前歯での剥離による渦管では回転方向が反対になることによるものと推察される.ただし,Lamb vector divergence φが正の場合,その近辺に渦管が見られなかったため,比較的渦度の弱い渦管に速い流速変化が生じたことによりLamb vector divergence φの高い値を示していると考えられる.
歯科治療において,摩擦音"s"発音に問題を生じさせないためには,最も上流側で渦管の生成が見られたsibilant grooveの形成に影響を及ぼさないことや,剥離による渦管生成を担う上下前歯の形状,位置関係を最適に保つ必要があると考えられる.ただし,最適な位置関係については,より詳しい調査が必要である.
被験者一名に対して,"s"発音時の詳細な口腔内形状を取得し,得られた気道データを元に6面体格子を作成し,LES解析を行うことで,口腔内の流れを調べた.ただし,コーンビームCTから得られた口腔内形状には,歯と歯の隙間等の微細な特徴のある形状が存在する.しかし,6面体格子によるマルチブロック構造格子では,それらの微細構造の表現が難しいため,省略された.さらに,口腔内面,特に口蓋部分の表面性状は滑らかな曲面で表現されているが,実際には,粗造で微細な非規則な溝が散見された.これら,本報告で行ったLES解析では捉えられなかった形状が,結果に及ぼす影響について調べるには,構造格子ではなく,数億要素レベルの非構造格子や,数十億要素レベルの直行格子によるLES解析が必要となると思われる.
6.おわりに
本稿では,数値流体力学シミュレーションによる,歯茎摩擦音"s"発音時の口腔内での流れと音源領域の可視化に関する研究を紹介した.歯茎摩擦音"s"音の発生は騒音研究分野と類似した手法を用いて行ったが,目的が低騒音化ではなく,適切な音を発生させなければならない点が異なる.今後のCFDおよびCAAの技術の発展によって,より多くの知見が得られることを期待している.
謝辞
本研究を推進するに当たり,大阪大学サイバーメディアセンターに計算機利用に関するご支援を頂いた.特に,下條真司教授,東田学助教には計算機環境の構築についてアドバイスを頂いた.LES解析ソフトFrontFlow/Blueの活用に際して,東京大学生産技術研究所の加藤千幸教授,GUO Yang博士,JR東日本株式会社の水島文夫博士,みずほ情報総研の山出吉伸氏にアドバイスを頂いた.グルノーブル大学Gipsa-labのXavier Pelorson博士,Annemie van Hirtum博士には様々な議論を通した研究的示唆を頂いた.大阪大学大学院基礎工学研究科の和田成生教授,埼玉大学院理工学研究科の中村匡徳先生には生体工学的アプローチの方法についてアドバイスを頂いた.大阪大学大学院歯学研究科の玉川裕夫先生にはコーンビームCTについてアドバイスを頂いた.ここに謝意を表する.
参考文献


