流れ 2009年4月号 目次
― 特集テーマ: 流体工学により解明される自然界,そこから生まれる新技術 ―
| リンク一覧にもどる | |
羽ばたきとオートローテーションにおける流れ
|
1.はじめに
「飛翔」は人間が身につけていない能力だけに,あこがれである.人類は,鳥を観るにつけて「あのように大空を飛べたらな」と思い描き,鳥の羽をまねたものを腕に付けぱたぱたと「羽ばたき」ながら走り,あるいは高いところから飛び降り,などして飛ぶことへの挑戦をしてきた.最初の飛ぶための試みは鳥の羽ばたきをまねることであった.しかし,ことごとく失敗であったことは知るところである.固定翼で飛ぶことが可能となってからしばらく羽ばたき翼は忘れられてきたが,近年マイクロエアビークル(MAV)に関心1,2)が向けられ,昆虫の羽ばたき1-6)に注目が集まるようになってきた.大ざっぱに言って体量が100g以下で飛行速度が10m/s以下のものでは,羽ばたきによる飛行である.MAV開発において,昆虫の羽ばたきを観察し,それを模倣することが正当なやり方であり,まさにそれが行われてきた7),8).この結果,その運動およびそれにともなう揚力取得方法(流れ場)は複雑かつ巧妙であることがわかってきた.大がかりな装置では実現できても昆虫程度に小型化することは簡単ではなさそうである.このため,いかに小型化に結びつくシンプルな方法で羽ばたきと同じように揚力を取得できるか?これを見いだすことが本研究の目的である.
2.羽ばたき
羽ばたき運動は図1に示すように,翼弦に対して垂直方向運動であるヒービング(対軸に対しての回転運動),翼弦に対して水平方向運動であるリード・ラグ(体軸に垂直な軸まわりの回転運動),体軸に水平な軸まわりの回転運動(ピッチング)であるフェザリングの3つの運動が組み合わさったものである.ヒービングとフェザリングの組み合わせ運動をとくにフラッピング(Flapping)という.蝶では体軸まわりの羽の回転角度が大きく,羽を打ち付けるクラップと引きはがすフリングを行う.
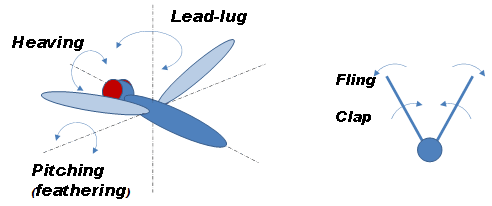
図1 羽ばたき運動を分解すると
これらの運動によって羽先端に渦(leading edge vortices)を形成し(delayed stall),その反力で揚力および推力を得る1-3).また,前の羽ばたき運動で形成された渦による誘起速度を利用し(wake capture) (この効果のほどはまだよくわかっていないが3)),さらに揚力を稼ぐ.また,羽の非定常運動とくにデッドポイントにおけるピッチング(羽ばたきの上死点においてピッチダウン,pronationと下死点においてピッチアップ,supination)によって,回転におけるマグヌス効果による付加揚力(Kramer効果3))が作用する.したがって,昆虫の羽ばたきの基本は渦の形成とその利用にある.
3.オートローテーション
羽ばたき運動する羽まわりの流れ場1-8)は,一様流れの中で図2に示すような矩形板が長軸まわりに回転する際に観察されるものとよく似ている.時計方向回転する矩形板まわりの流れ場の計測結果を図3に,2次元の渦法を用いた数値シミュレーション結果を図4に示す.無次元回転速度(スピンパラメータ)Sを次式のように表わす.
S = πNc / ( 60U ) (1)
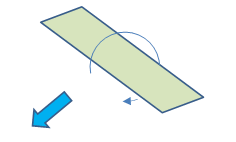
図2 オートローテーションしながら落下する矩形板
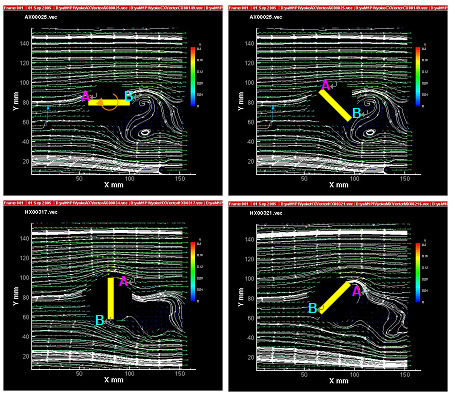
図3 オートローテンションする矩形板まわりの流れ計測結果.S=0.6.
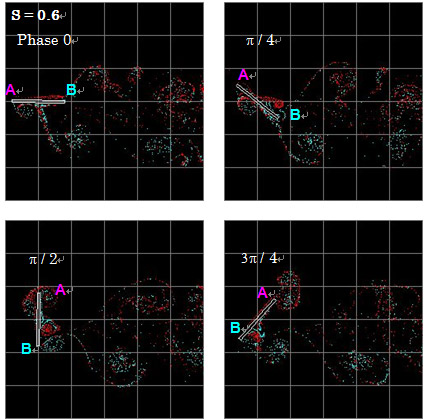
図4
オートローテンションする矩形板まわりの流れシミュレーション結果.S=0.6.
ここに,Nは毎分回転数(r.p.m.),cは矩形板の幅(コード長),Uは主流速度(矩形板の移動速度)である.主流速度に対する縁の速度の比を表している.実験から,S=0.6において一様流中において矩形板は自動的に回転する(オートローテーション)ことがわかった.数値シミュレーションにおいても同じ回転速度を用いている.両端にA, Bと名前を付け,回転の様子がわかるようにしてある.図3は流跡線のパターン,図4は渦点の分布としてπ/ 4回転毎の流れパターンを示してある.両者の結果は良く一致している.一様流に対して端Aはピッチアップ,端Bはピッチダウンの状態である.一周期前に形成された渦と現周期で形成される渦が板近傍で干渉しており,複雑な流れパターンであることがわかる.しかし,後方では周期的に交互に渦放出がなされ,あたかもカルマン渦列のようなパターンを示している.ただし,後流は下側に傾いているので,回転する板にはその反作用として揚力が作用していることがわかる.図5に最大揚力を示すときの流れ場を示す.最大揚力を示すときの流れを観ると上面に時計方向に回転する渦度をもったしっかりとした渦構造が存在している.この渦は端Aから放出されたものである.
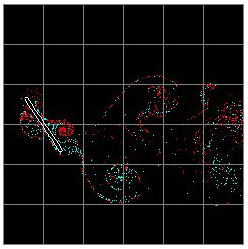
図5 最大揚力を示すときの流れ場.S =0.6.
(図をクリックすると動画が表示されます)
Sの違いによる揚力,抗力,モーメント,合力の比較を図6に示す.S >1では回転が速く,先行する端で発生した渦を後からくる端によって壊す結果,wake-captureがうまくできないために,合力は低くなっている.しかし,揚力だけについてみるとS <1の場合に比べ大きくなっており,回転によるマグヌス効果が作用しているものと考えられる.モーメントの方向は図より反時計方向であるので,矩形板の回転を止める方向に作用していることがわかる.これに対し,S <1では合力は先の場合に比べ1.5倍ほど大きくなっている.揚力は回転数が低くなるにつれて小さくなる.モーメントは矩形板の回転と同じ時計方向のものであるので,回転を持続するよう作用していることがわかる.ちなみに,体重の軽い昆虫の無次元羽ばたき周波数は0.25程度2)である.
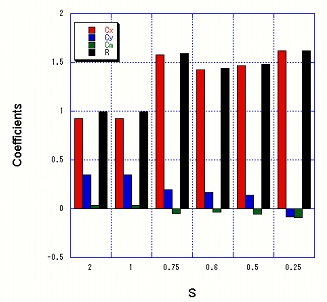
図6 Sの違いによる揚力係数Cy,抗力係数Cx,モーメント係数Cm,合力係数Rの比較
4.まとめ
昆虫程度の大きさおよび重量のMAVを作るならば,羽ばたきを用いるのが自然であるが,これをどの様に実現するかとなると,複雑な機構がおよび多くのモーターが必要となる.しかし,オートローテンションを用いれば,自動的に回転するのでモーターは必要ないことになる.回転数を下げるように回転軸にブレーキをかけ制御することで作用する力の大きさも変化させられるので,小型化の可能性が見えてきた.ただし,自力で離陸するにはやはり動力が必要であるので,その辺をどの様にするかが今後の課題である.
参考文献


