流れ 2009年4月号 目次
― 特集テーマ: 流体工学により解明される自然界,そこから生まれる新技術 ―
| リンク一覧にもどる | |
計測融合シミュレーションによる血流解析
|
1.はじめに
循環器系疾患は,生体内の血液の循環を担う心臓と血管に関わる疾患であり,現代の日本人の死因の約3割を占める.その発症および進展に対し,血流により生体組織に作用する力(血行力学)は,血管壁の機械的特性を変化させるなどの重要な役割を果たしている(1).そのため,血流場を正確かつ詳細に把握することが,より高度な診療に繋がると考えられる.
生体内の血流場の情報を得るには,X線CT,MRI,超音波診断装置による計測方法がある.しかし,現存する計測方法では,血流場の限られた情報しか得られず,時間・空間分解能や計測精度にも限界を有する.循環器系疾患の診断に最も幅広く用いられている超音波計測は,カラードプラ法により実際の血管の断面形状と共に血流動態を非侵襲かつリアルタイムに提供できるものの(2),その情報は血流の速度ベクトルを超音波ビーム方向に射影した成分(ドプラ速度)に限られる.また,圧力場や壁せん断応力の情報を得ることは困難である.
一方,各種画像診断装置を用いて血管の実形状を再構成し,血流の数値シミュレーションを行うことにより,血流場の詳細な情報を得ることができる(3).最近では,循環器系疾患の原因の解明や手術計画などの臨床応用に計算結果を用いる試みがなされている.しかし,実際の血流場を正確に再現するという目的に対しては,本質的に重要である計算条件の正確な設定が困難であることから,得られる計算結果が実際の血流場と完全には一致していないという問題がある.
流れの計測と数値シミュレーションがそれぞれ有する問題点の解決策として,制御理論における状態観測器の概念を流れ解析に適用した「流れのオブザーバ」が提案されている(4).これは,流れの計測の出力信号とそれに対応する数値シミュレーションの結果を比較し,両者の間の誤差に基づいて体積力や境界条件を数値シミュレーションにフィードバックし,コンピュータ上に実際の流れ場を再現する方法である.著者らは,実際の血流場を再現するために「流れのオブザーバ」を応用し,血流の超音波ドプラ計測と数値シミュレーションを融合した新たな血流解析手法として,超音波計測融合シミュレーション(5-8)を開発してきた(図1参照).
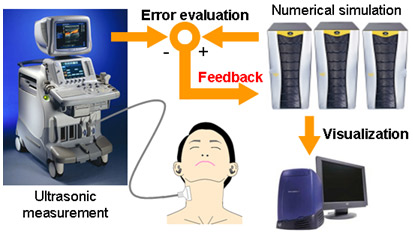
図1 超音波計測融合シミュレーションの概念図
2.超音波計測融合シミュレーション
超音波計測融合シミュレーションの基礎方程式は,非圧縮性ナビエ・ストークス方程式と圧力方程式である.
| (1) | |
| (2) |
ここで,u = (u, v, w)は速度ベクトル,pは圧力,ρは密度,μは粘度である.fは流れのオブザーバ独自の項であり,フィードバック信号を表す.超音波計測融合シミュレーションのフィードバック信号は,計測と計算によるドプラ速度の誤差に基づく仮想的な体積力として,以下の式により与える.
| (3) |
ここで,Kv*はゲイン(無次元値),Φdは速度ベクトルの超音波ビーム方向への射影関数,Uは代表速度,Lは代表長さ,添え字sおよびcは基準解(計測結果)および超音波計測融合シミュレーションの計算結果であることをそれぞれ表す.図2にフィードバック信号の作用の模式図を示す.実際の血流の速度ベクトルusと計算結果ucの間に誤差ueがある場合,超音波ドプラ計測を行うことにより,超音波ビーム方向に射影したドプラ速度の誤差Veの情報が得られる.この誤差を補償するように体積力fを作用させ,計算結果を実際の血流場に収束させる.計算手法としては,式(1)および(2)を有限体積法に基づいて離散化し,得られる差分方程式を解く.
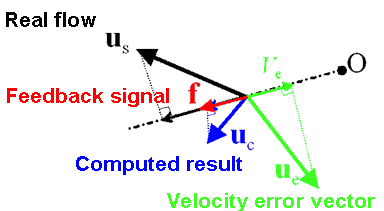
図2 フィードバック信号の作用の模式図
3.大動脈瘤内の血流を題材にした数値実験(5, 6)
超音波計測融合シミュレーションの計算精度を評価するため,下行大動脈に発症した動脈瘤内の3次元非定常の血流を計算対象とした数値実験を行った.数値実験では,実際の血流の状態に近い境界条件を与えて得られた数値解を基準解と定義し,誤差を含む境界条件を用いて実行する超音波計測融合シミュレーションによる基準解の再現について評価を行った.超音波計測融合シミュレーションでは,正確な境界条件が通常未知であることを考慮し,上流端には一様平行流,下流端には自由流出の条件を与えた.ただし,簡単のため,流量の時間変化は基準解のものと一致させた.また,この境界条件の差異により基準解に対して生じる誤差を減少させるため,動脈瘤内の全計算格子点において,ドプラ速度の誤差の情報に基づいてフィードバックを適用した.
得られた計算結果の一例として,図3に心拡張期における血管上の壁せん断応力分布を示す.いずれも良く似た計算結果が得られているが,基準解(図3(a))とフィードバックを適用しない通常の数値シミュレーション(図3(b))の間には,境界条件に起因する誤差が見られる(特に,矢印の位置).一方,超音波計測融合シミュレーション(図3(c))では,フィードバックの効果により,動脈瘤内において基準解の壁せん断応力を再現できており,血行力学の情報をより正確に把握することができる.
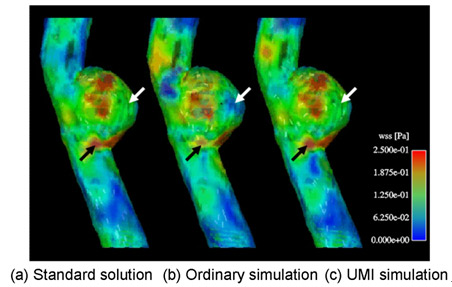
図3 数値実験による動脈瘤を有する血管上の壁せん断応力分布の比較
4.超音波計測融合シミュレーションシステムの開発(8)
超音波計測融合シミュレーションを循環器系疾患の診断に用いるため,システムの開発も行っている(図1参照).本システム開発は,企業と共同で行っており,血流の超音波計測融合シミュレーションをPC上で実行し,血流場や血行力学の情報を計測と同時にリアルタイムに可視化することを目指している.図4に,頚動脈のカラードプラ画像と本システムにより得られた2次元の超音波計測融合シミュレーションの結果を示す.これまでの超音波計測のみでは得ることが困難であった速度ベクトル(図4(b)の矢印)や圧力分布,壁せん断応力分布の情報を提供することが可能になった.
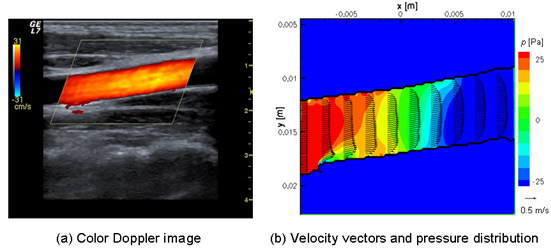
図4 頚動脈内血流の超音波計測融合シミュレーション結果
5.おわりに
超音波ドプラ計測と数値シミュレーションを融合した超音波計測融合シミュレーションは,血流場や血行力学をコンピュータ上に再現することができ,循環器系疾患のより高度な診断を実現する可能性を有している.これまでにその有用性を主に数値実験により確認し,システムの開発を行ってきた.現在は,実験による検証を行うと共に,様々な症例に本手法を応用し,汎用性の向上と疾患の有無による血行力学の変化の観察を行っている.
文献



