流れ　2010年4月号　目次

―　特集テーマ： 乱流遷移に携わる若手の研究紹介　― 亜臨界乱流遷移の理論的記述について 河原 源太（大阪大学） 実験的研究：主流乱れによる境界層の遷移過程について 松原 雅春（信州大学） 数値解析による研究：航空機の翼から発生する空力音と境界層不安定 跡部 隆（JAXA） 自由液膜内対流とその遷移過程 上野 一郎（東京理科大学） ヨーロッパでレイノルズの軌跡をたどる：円管内流れの遷移に関する研究 西 美奈（東京大学） 編集後記 編集後記（木上，帆足，塚原） 　｜　リンク一覧にもどる　｜

 

亜臨界乱流遷移の理論的記述について

河原源太 大阪大学

１．はじめに

　乱流遷移現象の予測と制御は，流体工学における最重要課題の１つである．流れの特性は，乱流遷移を経ることにより著しく変化する．したがって，遷移流れを制御することで，流れの特性の大幅な改善，例えば流動抵抗低減や伝熱促進などを実現することが期待される．

　 周知のように，乱流遷移には超臨界問題と亜臨界問題とがある．超臨界遷移の問題は比較的単純明快であり，現象は非線形微分方程式の解の（一連の）分岐問題に帰着され，臨界点（分岐点）及びその近傍では線形理論と弱非線形理論により現象の理論的記述が可能である．この種の遷移では，層流解からの一連の解の分岐により，層流状態が段階的に複雑化する．その代表例としては，レイリー・ベナール対流やクエット・テイラー流などがある．一方，亜臨界遷移の問題は極めて複雑である．第２節で述べるように，臨界点から遠く離れた場合あるいは臨界点が存在しない場合には，この種の遷移は有限振幅の撹乱により生じる本質的に非線形な問題であり，その理論的な取扱いは著しく難しくなる．亜臨界遷移では，層流状態から乱流状態へと急激に遷移が進行する．境界層流や平行平板間流れ，あるいは円管流や正方形ダクト流といった壁面剪断流は，亜臨界遷移により乱流に移行するのが一般的である．

　 本稿では，理論的な記述が困難である亜臨界乱流遷移の問題について議論したい．第２節において，なぜ亜臨界乱流遷移の問題が難しいのかを簡単に説明する．1990年以降，この難問に対して何度かブレイクスルーがあり，最近では亜臨界乱流遷移の理論的記述の糸口がある程度見えてきたように思われる．そこで第３節では，この問題に対する研究の進展をいくつかの代表的な壁面剪断流について紹介する．第４章では今後の研究の課題について手短に触れる．

２．なぜ亜臨界乱流遷移の問題は難しいのか？

　ここでは，平行平板間ポアズイユ流を例として取り上げる．この流れは圧力勾配により駆動される平行平板間の粘性流である．線形安定性理論により，この流れの層流状態（基本流）は，流路中心流速と流路高さの半分に基づくレイノルズ数が5772⁽¹⁾より大きくなると，無限小撹乱に対して不安定化することが示されている．この臨界点近傍では，弱非線形理論によりスチュワートソン・ランダウ方程式（振幅方程式）が求められており^(2),(3)，層流解から２次元定常進行波解⁽⁴⁾が亜臨界分岐（低レイノルズ数側に分岐枝が伸びる）することが示されている．線形理論で求められた臨界レイノルズ数5772を超えると，決して層流状態は実現されない．一方，この臨界レイノルズ数より小さい場合，すなわち亜臨界の場合，有限振幅の撹乱を層流に加えると，撹乱の振幅や形状に応じて，ときには層流状態が持続し，ときには乱流に遷移することになる．このように亜臨界の乱流遷移では，加える撹乱（初期条件）によってその後の流れの様子が全く異なるため，乱流遷移の本質を撹乱の性質によらずに簡潔に記述することは困難である．

 

３．最近の研究の進展

　前述の平行平板間ポアズイユ流の場合には，亜臨界問題ではあるが，基本流が無限小撹乱に対して不安定化するので，層流状態との有限のずれを有する非線形定常進行波解を，臨界点（分岐点）から数値計算により延長することが可能である．しかし，以下の３．１節，３．２節及び３．３節で述べる平行平板間クエット流，円管ポアズイユ流及び正方形ダクト流では基本流は線形安定であるため，層流解からの解の分岐はあり得ない．ゆえに，層流からの解の分岐を追跡することによって非線形解を求めることは不可能である．このため，これらの流れの乱流遷移の解明は流体力学における難問とされてきた．しかし，平行平板間クエット流における非線形定常解⁽⁵⁾の発見を契機に，以下に記すように，最近これらの流れに関する研究が大きく進展している．３．４節では平行平板間ポアズイユ流に関する最近の結果を紹介する．

 

３．１　平行平板間クエット流

　平行平板間クエット流では，有限撹乱による乱流遷移が認められるのは，平板の速度差の半分と流路高さの半分に基づくレイノルズ数がおよそ320以上においてである⁽⁵⁾．したがって，レイノルズ数がこの値を超えると，層流状態と乱流状態のいずれも実現することになる．すなわち，流れの状態が空間の１点として表現される相空間では，層流アトラクターと乱流アトラクター（あるいは乱流サドル）とが共存することになる．これら２つのアトラクターの吸引領域間には境界が存在し，相空間における初期点（初期状態）が境界の層流側，乱流側のどちらに位置するかに従って，その後の時間発展の結果流れが層流化するか乱流が実現するかが決する．

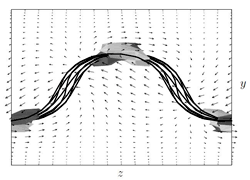
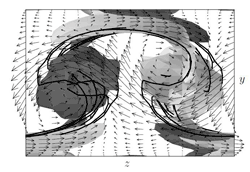
　Nagata⁽⁶⁾は，その後の研究の進展をもたらす新奇のアプローチにより，上述した平行平板間クエット流の困難を解決した．平板間クエット流を，スパン方向に向いた軸回りに一定速度で回転させるものとする．無回転の場合には基本流は線形安定であるが，基本流の渦度と反平行に適度の回転を与えると，回転平板間クエット流は無限小撹乱に対して不安定化する．Nagata⁽⁶⁾は，クエット流を回転させることによって得た臨界点から分岐する非線形の（流れの方向に一様な）２次元定常解を数値的に求め，さらにはこの２次元解から分岐する３次元定常解を数値的に求めた．こうして得られた３次元解を，クエット流に与えた回転率を徐々に減少させながら計算し，回転率がゼロの状態，すなわち非回転クエット流における非線形の３次元定常解を得ることに成功した．このNagata⁽⁶⁾の解は，流れ方向とスパン方向に周期性を有し，レイノルズ数がおよそ127⁽²⁷⁾においてサドル・ノード分岐により生成され，それより大きいレイノルズ数では，同一レイノルズ数において層流からのずれが小さい下分枝解とずれの大きい上分枝解の対をなす．図１に著者らにより再計算されたNagataの解の下分枝と上分枝を示す⁽⁷⁾．この定常解の空間構造が，乱流遷移や発達乱流において認められる流れ方向渦とストリークによって特徴づけられることがわかる．

(a)	(b)
図１　Nagata(6)の定常解の下分枝(a)及び上分枝(b)(7)．１周期箱における流れ（x）方向渦度の等値面（白が正（時計回り），灰色が負（反時計回り））が示されている．また，xが一定の異なる面での流れ方向速度がゼロの等値線と流れに垂直（y，z）方向の速度ベクトルが示されている．

 

　最近，相空間においてこの定常解の下分枝はただ１つの不安定方向をもち，この解及びその安定多様体が，前述した層流アトラクターと乱流アトラクターとの吸引領域境界を形成することが示された⁽⁸⁾．もしこの吸引領域境界が同定されれば，層流と乱流の境界あるいは乱流遷移をもたらす有限振幅撹乱の振幅や形状に関する完全な情報が得られることになる．しかし，極めて次元の高い安定多様体の大域的な同定は困難であり，もし同定できたとしても，その情報量は膨大であり，そこからの亜臨界乱流遷移の本質の抽出が必要となろう．

　実は，この層流と乱流の吸引領域境界に関する報告以前に，著者は平板間クエット流の静穏な時間周期解⁽⁹⁾とその安定多様体が層流アトラクターと乱流アトラクターとの吸引領域境界を形成することを見出した⁽¹⁰⁾．図２は，この時間周期解の線形安定性解析によって得られた１次元不安定固有空間上に微小撹乱を与えた際の流れの時間発展を示したものである．不安定固有空間上に与える撹乱の向きの違いによって，層流に移行する（破線），あるいは乱流に遷移する（実線）することになる．したがって，周期解（青い閉曲線）とその安定多様体が層流と乱流の境界を形成していることがわかる．最近では，平板間クエット流を模擬した低自由度力学系において，相空間における層流と乱流の境界（edge of chaosとよばれることがある）を大域的に同定し，低レイノルズ数ではそれが上で見たように周期解の安定多様体に一致することが観測されており⁽¹¹⁾，またナビエ・ストークス方程式に従う力学系に対しても層流と乱流の境界に関する研究が行われつつある⁽¹²⁾．

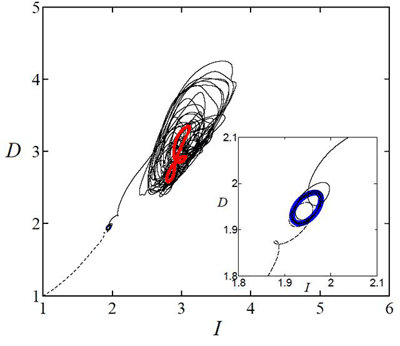図２　Kawahara-Kida(9)の静穏周期解（青）の不安定固有空間に微小撹乱を与えた際の流れの時間発展(10)．Dはエネルギー散逸率，Iはエネルギー注入率を表す．これらは対応する層流状態の値で規格化されている．赤い閉曲線は乱流と類似した性質を有する活発周期解である．

 

３．２　円管ポアズイユ流

　円管ポアズイユ流では，十分に大きい撹乱を層流状態に与えれば，管断面平均流速と管直径に基づくレイノルズ数がおよそ2000以上で乱流遷移が起こることが古くから知られている．乱流遷移が可能となる下限レイノルズ数は，より正確には1760から2300の間の値である⁽¹³⁾．最近，円管流においても非線形３次元定常進行波解が発見されて注目を集めている^(14),(15)．この定常進行波解は，管軸回りの離散回転対称性をもち，その空間構造は平板間クエット流のそれと同様に流れ方向渦とストリークによって特徴づけられる．この解はレイノルズ数がおよそ1251においてサドル・ノード分岐によって現れ，それより大きいレイノルズ数では下分枝と上分枝からなる．この最低レイノルズ数をもたらす進行波解は，周方向波数が3（2π/3回転対称），つまり３本のストリークと３対の互いに逆回転する流れ方向渦を有する．最近，回転対称性をもたない非線形３次元定常進行波解も発見され，そのうちの鏡像対称解がさらに低いレイノルズ数773でのサドル・ノード分岐によって発生することが示されている⁽¹⁶⁾．

　上で見た平板間クエット流の場合には，定常解あるいは周期解の相空間での不安定方向はただ１つであり，それらの解の安定多様体が層流と乱流の境界を与える．したがって，この場合，その境界（不変集合）内でのアトラクター（edge stateとよばれることがある）は必然的に定常下分枝解⁽⁶⁾や静穏周期解⁽⁹⁾となり，層流と乱流の境界内での流れの動力学は非常に単純である（単なる定常解あるいは周期解への漸近）．一方，円管ポアズイユ流においては，定常進行波解の不安定方向は２つ以上あると考えられ，層流と乱流の境界内に埋め込まれた進行波解に流れの状態が漸近することは許されず，境界内での流れの動力学はカオス的となることが観測されている⁽¹⁷⁾．

 

３．３　正方形ダクト流

　 矩形断面を有するダクト内の流れには臨界アスペクト比が存在し，アスペクト比が臨界値（およそ3.2）より大きい場合には層流状態は線形不安定であるが，それより小さい場合には線形安定となる⁽¹⁸⁾．したがって，アスペクト比が1の正方形ダクト流は３．１，３．２節で述べた平板間クエット流や円管ポアズイユ流と同様，任意のレイノルズ数において無限小撹乱に対して安定となる．ここでは正方形ダクト流に関する最近の結果を紹介する．

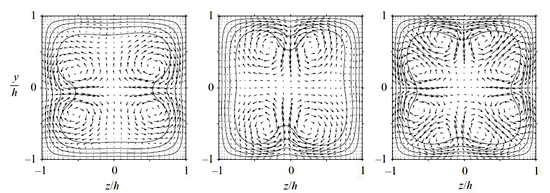
　著者らは流れ方向周期がダクト幅のおよそ0.4倍から13倍の計算領域において正方形ダクト乱流の直接数値シミュレーションを行い，乱流が持続する下限レイノルズ数（ダクト断面平均流速とダクト幅の半分に基づく）がおよそ1100であることを観測した⁽¹⁹⁾．比較的流れ方向周期の短いダクト（流れ方向周期がダクト半幅hのおよそ3倍）において乱流が持続する下限レイノルズ数付近では，１本の低速ストリークと１対の千鳥配列した互いに逆回転する流れ方向渦がダクトの対向する２壁面上のみに存在する状態が現れる．その結果，図３に示すように，平均二次流れは，周知の８つの渦をもつ流動パターン⁽²⁰⁾ではなく，４つの渦（と２つの低速領域，つまり図３(a)，(b)の湾曲した等値線）をもつ特異なパターンを示す⁽¹⁹⁾．

(a)	(b)	(c)
図３　乱流が持続する下限レイノルズ数近傍での正方形ダクト乱流の平均流(20)．流れ（x）方向平均速度が等値線，流れに垂直（y，z）方向の平均速度がベクトルで示されている．(a)はある時間間隔での平均，(b)は(a)と異なる時間間隔での平均，(c)は(a)と(b)の時間間隔を含む長時間での平均を表す．

 

　最近，上で述べた，乱流が持続する下限レイノルズ数付近に固有な４つ渦パターンを示す流れに対応する正方形ダクトの非線形３次元定常進行波解が，沖野・永田⁽²¹⁾によって発見された．彼らの解は，前述したNagata⁽⁶⁾のアプローチと同様の手法で，一様な内部発熱を伴う鉛直正方形ダクト流の層流状態の臨界点⁽²²⁾から分岐した非線形定常進行波解を内部発熱がゼロの状態に延長することで求められたものである．

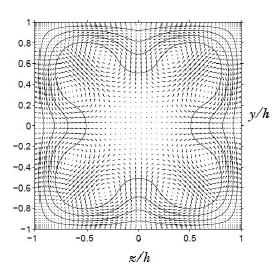
　また，より最近，著者らは，１本の低速ストリークと１対の互いに逆回転する流れ方向渦が４壁面上に存在する流れを示す正方形ダクトの非線形定常進行波解を発見した⁽²³⁾．図４にこの進行波解の流れの構造と流れ方向平均で得られた平均二次流れを示す．この定常進行波解は，乱流状態に現れる８つ渦パターンの平均二次流れ⁽²⁰⁾と同様の二次流れをもち，ナビエ・ストークス方程式が許容する非線形平衡状態と乱流二次流れを関連づける点で興味深い．この種の解と正方形ダクトにおける乱流遷移との関連性が明らかにされれば，乱流二次流れの生成機構の理論的解明につながると考えられる．

(a)	(b)
図４　４本の低速ストリークと４対の互いに逆回転する流れ（x）方向渦をもつ正方形ダクト流の定常進行波解(23)．(a) 壁面y/h=-1上の低速ストリークと流れ方向渦．灰色の曲面は流れ方向速度の等値面，濃い灰色と黒の曲面は正（時計回り）と負（反時計回り）の流れ方向渦度の等値面を表す．(b) 流れ方向に平均した速度の，流れ方向成分の等値線と流れに垂直（y，z）方向成分のベクトル線図．

　正方形ダクト流に関しては，層流と乱流の境界に関する研究はまだ行われていないが，上で紹介したように複数の非線形定常進行波解が既に発見されているので，層流・乱流境界に関する研究が今後急速に進展するものと期待される．３．１節，３．２節で紹介した平板間クエット流及び円管ポアズイユ流と比べれば，正方形ダクト流は周囲を壁面に囲まれている点で円管流に近い．よって，層流と乱流の境界内での流れの漸近先は定常進行波ではなくカオスアトラクターであるものと予想される．

 

３．４　平行平板間ポアズイユ流

第２節において平板間ポアズイユ流について簡単に触れた．この流れでは層流状態からの２次元定常進行波の分岐が起こる⁽⁴⁾．この２次元解の線形不安定性，いわゆる二次不安定性⁽²⁴⁾によって，微小撹乱による平板間ポアズイユ流の乱流遷移については比較的よい理解が得られている．しかし，振幅の大きい撹乱で生じる亜臨界遷移の様相は，これとは大きく異なる．

平板間ポアズイユ流の亜臨界問題に対しては，Itano-Toh⁽²⁵⁾及びWaleffe^(26),(27)による先駆的な研究により，円管ポアズイユ流や正方形ダクト流以前に非線形３次元定常進行波が求められている．Waleffe⁽²⁷⁾は，平板間ポアズイユ流において求めた彼の定常進行波解が，境界条件を変化させながらそれを追跡することによって，平板間クエット流に対するNagata⁽⁶⁾の定常解に接続できることを示した．すなわち，平板間のポアズイユ流とクエット流に対するそれぞれの非線形解は同一であると言える．亜臨界レイノルズ数においては，これらの解の下分枝の不安定多様体は，クエット流と同様に，層流と乱流の吸引領域境界を形成するものと考えられる⁽²⁵⁾．したがって，有限振幅撹乱に関する亜臨界遷移では，古くからHerbert⁽⁴⁾によって得られていた２次元の進行波解と言うよりもむしろ，層流解からは分岐しないItano-Toh⁽²⁵⁾及びWaleffe^(26),(27)の３次元進行波解が重要となる．

 

４．まとめ

　 以上で述べたように，1990年以降，亜臨界乱流遷移を示す典型的な壁面剪断流である平板間ポアズイユ流，平板間クエット流，円管ポアズイユ流及び正方形ダクト流では，非線形３次元の定常進行波解や周期解が存在することが明らかにされてきた．これらの解は相空間において安定方向と不安定方向をもつサドルである．ある解からその不安定方向へ伸びる不安定多様体が，その解自身あるいは他の解の安定多様体と接続する場合（ホモクリニック接続あるいはヘテロクリニック接続）には，解と解とを結ぶ大域的な軌道が生成される．このような相空間の広範囲に及ぶ大域的な軌道が多数生じてネットワークを形成すると，流れは多様な状態（解）の間を彷徨することが可能となり，複雑な流れの振舞いが現れ得る．さらに，ある解の不安定多様体とその解自身あるいは他の解の安定多様体が横断的に交差すると，無数のホモクリニック点あるいはヘテロクリニック点（不安定多様体と安定多様体との交点）を生じて複雑な相空間構造をもたらし，またいわゆるスメールの馬蹄形写像からの類推により，カオス的な挙動が実現されるものと考えられる．したがって，乱流遷移に対して今後さらに一歩踏み込んだ議論を行うためには，定常進行波解や周期解の不安定多様体を大域的に数値計算する必要があろう．この方向の研究としては，平板間クエット流において定常解のヘテロクリニック接続⁽²⁸⁾や周期解の不安定多様体⁽²⁹⁾に関する研究が最近行われている．

本稿では，特に断ることなく，力学系として取り扱うことのできる小寸法の周期箱における壁面剪断流，言わばミニマル流^{(30),(31),(19)}の乱流遷移を考えてきた．もし実験で観測される流れに匹敵するほどにその寸法が大きくなると，平板間クエット流や平板間ポアズイユ流においては斑点⁽⁵⁾あるいは斜め縞⁽³²⁾が，円管ポアズイユ流や正方形ダクト流ではパフ⁽³³⁾が乱流遷移時に現れることになる．これらの構造は空間に局在し，それらの長さスケールは壁近傍のストリークや流れ方向渦のスケール，すなわちミニマル流の寸法に比べずっと大きい．したがって，ここで紹介した小周期箱における定常進行波解や周期解によって，大領域の壁面剪断流で生じる乱流遷移を直接捉えることはできない．今後はこのギャップを埋めることが望まれる．最近，この方面では，大周期箱の平板間クエット流において，空間的に局在した斑点構造をもつ相空間での層流・乱流境界内のカオスアトラクター（edge state）に関する研究⁽³⁴⁾やスパン方向に局在した空間構造をもつ定常解や定常進行波解に関する研究⁽³⁵⁾が行われている．

 

参考文献

(1)	Orszag, S. A., J. Fluid Mech., Vol. 50 (1971), pp. 689-703.
(2)	Stuart, J. T., J. Fluid Mech., Vol. 9 (1960), pp. 353-370.
(3)	Watson, J., J. Fluid Mech., Vol. 9 (1960), pp. 371-389.
(4)	Herbert, T., AGARD, (1977), cp-224,3.
(5)	Dauchot, O and Daviaud, F., Phys. Fluids, Vo. 7 (1995), pp. 335-343.
(6)	Nagata, M., J. Fluid Mech., Vol. 217 (1990), pp. 517-527.
(7)	Jimenez, J., Kawahara, G., Simens, M., Nagata, M. and Shiba, M, Phys. Fluids, Vol. 17 (2005), 015105.
(8)	Wang, J, Gibson, J. and Waleffe, F., Phys. Rev. Lett., Vol. 98 (2007), 204501.
(9)	Kawahara, G. and Kida, S., J. Fluid Mech., Vol. 449 (2001), pp. 291-300.
(10)	Kawahara, G., Phys. Fluids, Vol. 17 (2005), 041702.
(11)	Skufca, J. D., Yorke, J. A. and Eckhardt, B., Phys. Rev. Lett., Vol. 96 (2006), 174101.
(12)	Schneider, T. M., Gibson, J. F., Lagha, M., Lillo, F. D. and Eckhardt, B, Phys. Rev. E, Vol. 78 (2008), 037301.
(13)	Kerswell, R. R., Nonlinearity, Vol.18 (2005), pp. R17-44.
(14)	Faisst, H and Eckhardt, B., Phys. Rev. Lett., Vo. 91 (2003), 224502.
(15)	Wedin, H. and Kerswell, R. R., J. Fluid Mech., Vol. 508 (2004), pp. 333-371.
(16)	Pringle, C. C. T. and Kerswell, R. R., Phys. Rev. Lett., Vol. 99 (2007), 074502.
(17)	Schneider, T. M., Eckhardt, B. and Yorke, A., Phys. Rev. Lett., 99 (2007), 034502.
(18)	Tatsumi, T. and Yoshimura, T., J. Fluid Mech., Vol. 212, pp. 437-449.
(19)	Uhlmann, M., Pinelli, A., Kawahara, G. and Sekimoto, A., J. Fluid Mech., Vol. 588 (2007), pp. 153-162.
(20)	Pinelli, A., Uhlmann, M., Sekimoto, A. and Kawahara, G., J. Fluid Mech., Vol. 644 (2010), pp. 107-122.
(21)	沖野真也，永田雅人，日本流体力学会年会2009．
(22)	Uhlmann, M. and Nagata, M., J. Fluid Mech., Vol. 551 (2006), pp. 387-404.
(23)	Uhlmann, M., Kawahara, G. and Pinelli, A., in Advances in Turbulence XII, (2009), pp. 585-588, Springer.
(24)	Herbert, T., Annu. Rev. Fluid Mech., Vol. 20 (1988), pp. 487-526.
(25)	Itano, T. and Toh, S., J. Phys. Soc. Jpn., Vo. 70 (2001), pp. 703-716.
(26)	Waleffe, F., J. Fluid Mech., Vol. 435 (2001), pp. 93-102.
(27)	Waleffe, F., Phys. Fluids, Vol. 15 (2003), 1517.
(28)	Halcrow, J., Gibson, J. and Cvitanovic, P., J. Fluid Mech., Vol. 621 (2009), pp. 365-376.
(29)	van Veen, L., Kawahara, G. and Matsumura, A., (2010), in preparation.
(30)	Jimenez, J. and Moin, P., J. Fluid Mech., Vol. 225 (1991), pp. 213-240.
(31)	Hamilton, J. M., Kim, J. and Waleffe, F., J. Fluid Mech., Vol. 287 (1995), pp. 317-348.
(32)	Prigent, A., Gregorie, G., Chate, H., Dauchot, O and van Saarloos, W., Phys. Rev. Lett., Vol. 89 (2002), 014501.
(33)	Wygnanski, I. J. and Champagne, F. H., J. Fluid Mech., Vol. 59 (1973), pp. 281-335.
(34)	Duguet, Y., Schlatter, P. and Henningson, D., Phys. Fluids, Vol. 21 (2009), 111701.
(35)	Schneider, T. M., Gibson, J. and Burke, J., Phys. Rev. Lett., Vol. 104 (2010), 104501.