流れ　2010年4月号　目次

―　特集テーマ： 乱流遷移に携わる若手の研究紹介　― 亜臨界乱流遷移の理論的記述について 河原 源太（大阪大学） 実験的研究：主流乱れによる境界層の遷移過程について 松原 雅春（信州大学） 数値解析による研究：航空機の翼から発生する空力音と境界層不安定 跡部 隆（JAXA） 自由液膜内対流とその遷移過程 上野 一郎（東京理科大学） ヨーロッパでレイノルズの軌跡をたどる：円管内流れの遷移に関する研究 西 美奈（東京大学） 編集後記 編集後記（木上，帆足，塚原） 　｜　リンク一覧にもどる　｜

 

ヨーロッパでレイノルズの軌跡をたどる -円管内流れの遷移に関する研究-

西　美奈 東京大学

１．はじめに

　筆者は2001年10月から2009年2月までの約7年半をドイツのエアランゲン(図1)で大学(院)生として過ごした. エアランゲンはバイエルン州北部にある人口約10万人の都市でありドイツを代表する企業の一つ，ジーメンスの本社が置かれる．大気汚染問題への取り組みの一環として街の中心が歩行者天国になっており人口に対して自転車台数がとても多い街としても知られる.

筆者は図2のエアランゲン大学(正式名称, フリードリヒ・アレクサンダー大学 エアランゲン-ニュルンベルク)で修士課程と博士課程を修了した. 大学入学前2ヶ月間のドイツ語学研修を含む留学体験はこちら⁽¹⁾に詳しいので興味のある方は参照されたい. 本稿では, エアランゲン大学流体力学研究室で行った筆者の博士課程の研究成果⁽²⁾を引用しつつ，工業的に且つ社会的に重要でありながら未解決の流体力学基本問題の一つ，円管内流れの遷移について最近の研究動向等も交えて紹介できればと思う.

 

図1　街の中心に建つヒューゲンノッテン教会の最上階から眺める
エアランゲンの街と筆者

図2　エアランゲン大学メインホール(旧ブランデンブルク=
バイロイト辺境伯宮殿)と大学創立者フリードリヒの像

２．円管内流れの遷移に関するレイノルズの実験と臨界レイノルズ数

　円管内流れ(以下，円管流)は流体力学における基本流れの一つであり，円管流の遷移に関する研究は良く知られた1883年のレイノルズの実験 ⁽³⁾以降，多くの研究者によりなされてきた. 図3はレイノルズが行った円管流遷移の水槽実験のスケッチである. 彼は円管内に一筋のインクを流し，その挙動で流れが遷移する様子と遷移が層流から乱流，また乱流から層流の双方向に間欠性を持って発生する事を図4の様に示した．そして, 流体の動粘性係数と管の直径及び断面平均流速から求まる無次元数―今日ではレイノルズ数として知られる―を導入して遷移の有無を評価し，その値が約2300を上回ると円管流に乱流遷移が生じる (より正確に言うと, レイノルズ数約2300以下では円管流は層流であり続ける) 事を示した．同時にレイノルズは，流入状態に留意すればレイノルズ数が12000程度まで円管流が層流に保たれる事も示した.

 

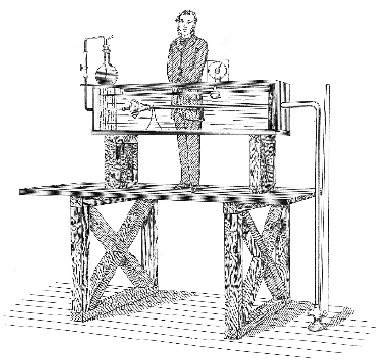
図3　マンチェスター大学におけるレイノルズの円管流遷移実験装置⁽³⁾

 

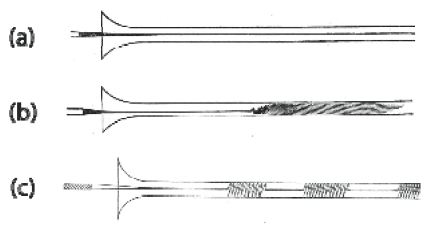
図4　レイノルズが示した(a)層流と(b)乱流の場合のインク筋の挙動と
(c)遷移流の間欠性の様子⁽³⁾

 

一般に乱流遷移が起こるレイノルズ数は臨界レイノルズ数と呼ばれ円管流遷移の場合には二種類存在する. 一つはそれ以下では円管流を乱流状態で維持できない下限の数であり，もう一つは円管流を層流に保ち得る上限の数である. レイノルズにより示された後者の臨界レイノルズ数(約12000)は後年, Pfenninger⁽⁴⁾によって10⁵まで高められる事が実験的に示されたが, 完全発達した円管流が微小撹乱に対して有限のレイノルズ数では線形安定である事を考慮すると，この値は今後更に高まるものと予想される. しかし一方で実際の円管流においては如何に注意深く外乱の侵入を防いだとしても，無限に高いレイノルズ数まで層流が維持され続けるとは考え難く，円管流の上限の臨界レイノルズ数が実際に有限の値を持つか否かについては現在も多くの議論の余地が残されている.

　 一方，円管層流を乱流遷移に導く臨界レイノルズ数は外乱の種類や強さに当然依存する．筆者ら⁽⁵⁾は図5に示される装置を用いて例えば外乱強度と臨界レイノルズ数の相関を調べた．実験は，質量流量コントローラで制御した空気流を定常に直径Dの円管に送り込み，下流部に設置した高さhの薄い金属リングで外乱を与えて行われた. 外乱強度は種々のhのリングを用いる事で変化させた．この実験の重要なポイントの一つは，質量流量コントローラに内蔵された臨界ノズルにより流れをチョークさせて質量流量を制御している点である．何故なら通常の流量コントローラでは遷移が生じた時の圧力降下によって流量(従ってレイノルズ数をも)が変化してしまうからである．図6は，リング高さと臨界レイノルズ数の関係を示しており，筆者らは無次元化した外乱強さ(hD^-1)は臨界レイノルズ数の-0.5乗に比例する事を実験的に且つ解析的に示した⁽⁵⁾が, 噴流という性質が異なる外乱を与えたHofら⁽⁶⁾の実験結果では外乱強度は臨界レイノルズ数の-1乗に比例するとしている. この乗数に関しては外乱強度の定量化等が試みられており⁽⁷⁾，統一的な見解を得るために, 今後の更なる解明が期待される. もう一方の乱流維持が可能な下限の臨界レイノルズ数に関しては本稿の第4節で ’乱れ’ のライフタイムの議論と合わせて論じる.

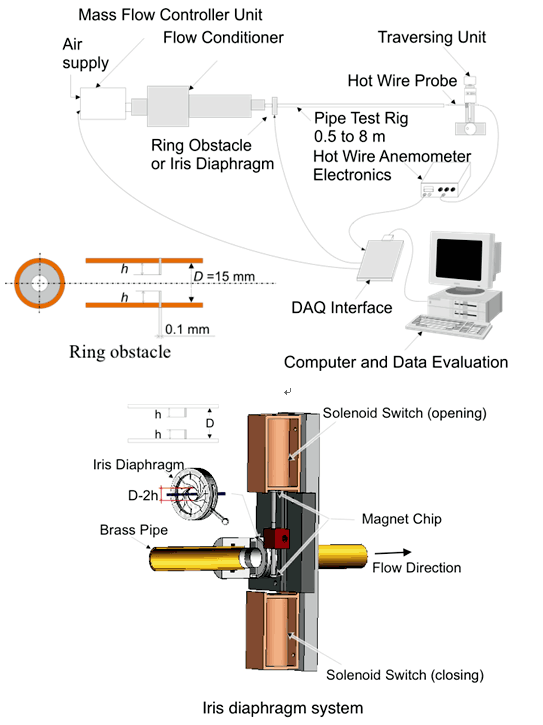
図5　筆者らが円管流の遷移実験に用いた装置の概略図⁽⁵⁾

 

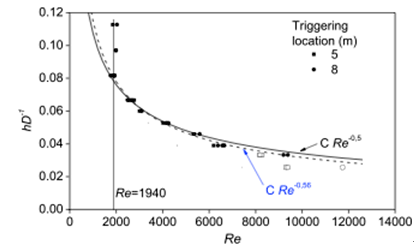
図6　完全発達流れに与えた外乱強度(縦軸)と臨界レイノルズ数(横軸)の関係⁽⁵⁾

 

３．パフとスラグ

　円管流の遷移の特徴の一つはレイノルズが模式的に示した様に(図4c参照)間欠性にある. その間欠的な管内遷移流の構造は大きく分けて二種類存在する事はWygnanskiら⁽⁸⁾により示された. 一つは, 低レイノルズ数領域(約Re < 3000)で大きな外乱を与えた場合にだけ発生するパフ(puff), もう一つは高レイノルズ数領域(約Re > 3000)で小さな外乱でも発生するスラグ(slug)である．パフ及びスラグの発生領域をレイノルズ数と外乱強さに対して表示すると図7の様になる．また，図8には円管中心軸上で測定した典型的なパフとスラグの軸方向速度の時間変化を，Willisら⁽⁹⁾の数値計算による構造可視化図と共に示した. 層流から遷移(乱)流に入ると管中心軸上の速度は減少するが，速度低下の勾配が比較的緩やかなのがパフ，急なのがスラグである．その他パフとスラグの違いは内部の乱流構造に見られ，例えば乱流の強度や非等方性に特徴的に表れる⁽²⁾が，限られた紙面の都合上本稿では割愛する．

　 では，パフとスラグは一体どの様に発達乱流へと遷移して行くのであろうか．この点について筆者らは再び図5の装置を用いて調べた. この実験では, アイリスダイアフラムを用いて任意の時刻と強度で外乱を円管流に与えた．それによりパフやスラグを人為的に発生させ，下流にて熱線流速計で軸方向速度を計測した. その時，管内のパフやスラグの伝播速度や構造変化を調べる為に管長を随時変化させて管出口で計測を行った．図9，10はそれぞれスラグ及びパフの通過による円管中心速度の時間変化を示しており，Lは外乱発生源のアイリスダイアフラムから管出口までの距離である．図9よりスラグは移流形態がレイノルズ数に依存せず，上流と下流方向に乱れが伝播する為流れ方向のスケールを増加させつつ下流方向へ移流する．一方パフは図10に示される様にレイノルズ数によって下流方向への移流形態が多様で，図10aのRe = 2310の場合は単一パフがそのまま移流するが図10bのRe = 2495の場合はL = 5m付近で分裂しその後形を変えずに移流し，図10cのRe = 2680の場合はL = 3m付近で分裂しその後も分裂を繰り返す形でスラグへと発達しながら移流する様子が示されている．この様な分裂パフの存在はこれまで確認されてはいたが, 構造や発生機構についての議論はほぼ皆無だった．しかし本研究により例えば分裂パフは一つのパフが分裂する過程でのみ発生する事やパフからスラグへの遷移過程で必ず生じる事等が新たに見出された. また現在でも管内の遷移現象は確率的か決定的か研究者間で意見が割れる中，図11に示される様に分裂パフの発生頻度(同一条件で数百回発生させたパフの内何個のパフが任意の下流の点までで分裂したかを示す割合)がレイノルズ数の上昇に伴って体系的に増加する事実は, 分裂パフの発生が確率的である事を如実に示す重要な結果と言える⁽¹⁰⁾.

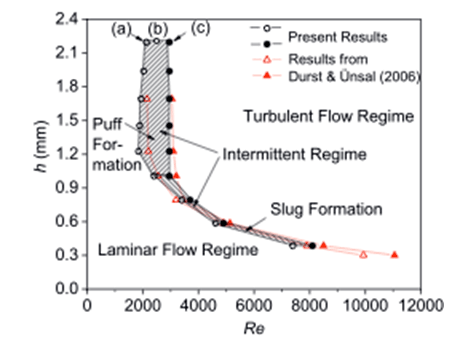
図7　レイノルズ数と外乱の関係とパフとスラグの発生領域⁽⁵⁾

 

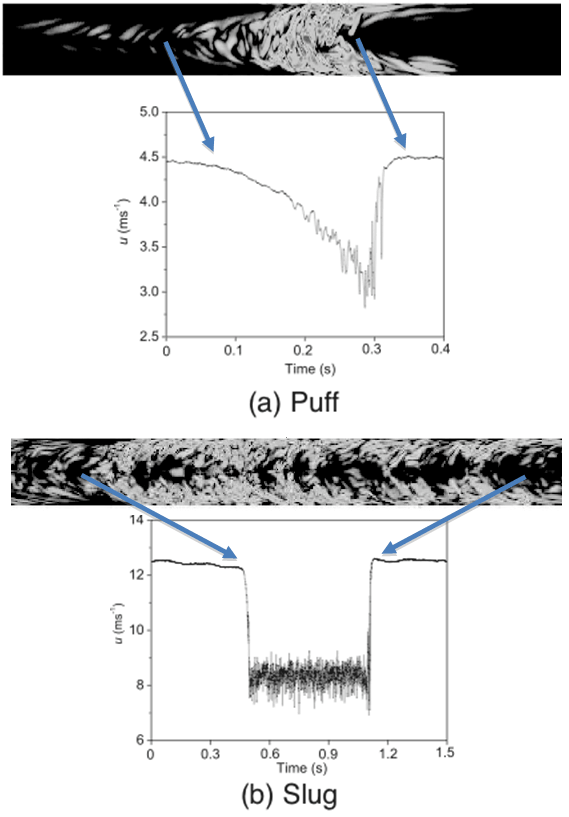
図8　(a)パフと(b)スラグの通過に伴う管中心軸上の流速時間変化⁽⁵⁾と
数値計算による内部構造可視化結果⁽⁹⁾
(ただし可視化図は軸方向長さが縮小されている)

 

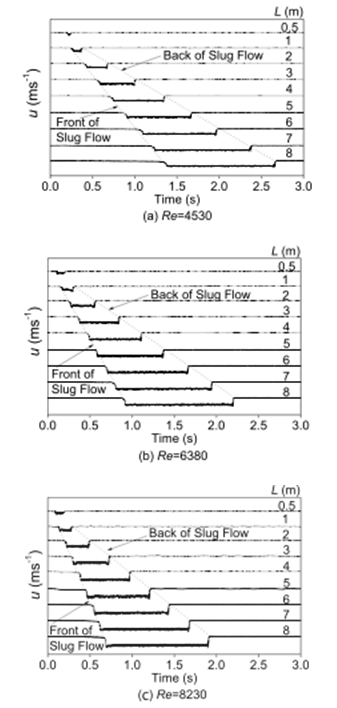
図9　スラグの管内発達過程⁽⁵⁾ (a) Re = 4530, (b) Re = 6380, (c) Re = 8230

 

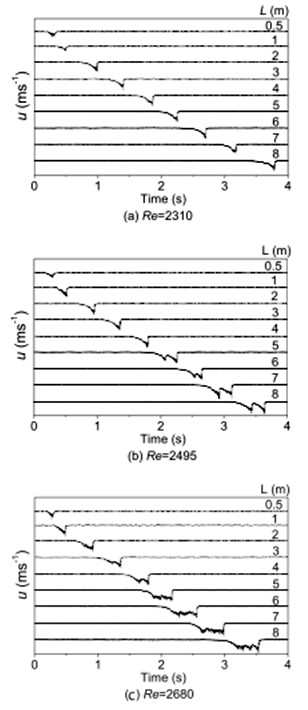
図10　パフの管内発達過程⁽⁵⁾ (a) Re = 2310, (b) Re = 2495, (c) Re = 2680

 

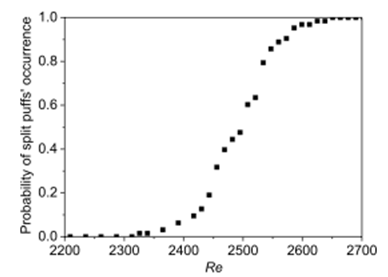
図11　レイノルズ数増加に伴う分裂パフの発生頻度の増加⁽¹⁰⁾

４．ライフタイムと下限臨界レイノルズ数

　外乱によって発生した円管流の乱れの発達挙動はレイノルズ数に依存する．この乱れを管内で維持できる最小のレイノルズ数が本稿第2節で触れた下限臨界レイノルズ数に相当し，レイノルズを初めとして種々の提案があるが未だに結論付けられていない．そこで，外乱を与えてから発生した乱れが散逸するまでの時間(ライフタイム)を指標としてこの下限臨界レイノルズ数を求める実験を行った．乱れのライフタイムは管の上流と下流の2点間の静圧差Δpの時間的な軌跡を取る⁽¹¹⁾という大変シンプルな手法で測定された．前節同様，実験は数百回繰り返して行いアンサンブル平均結果からライフタイムを得た．その時に，管出口の速度計測により乱れが管内で完全に散逸した事は毎計測ごとに確認された．図12はライフタイムの逆数とレイノルズ数の関係を表す. 図12には二種類のライフタイムLT_fullとLT_dissが示されるが，前者は外乱を与えた時刻から乱れの散逸までの時間で後者は乱れが発達し終えた時刻から散逸までの時間を示す．LT_fullとLT_dissのどちらもレイノルズ数の変化に対して同じ傾向を示す事は乱れの発達(つまり散逸直前の初期状態)が一様であった事を示すが詳細はこちら⁽²⁾に譲る．

　 図12aより，レイノルズ数の増加に伴いRe < 1560でLT^-1は緩やかに減少するがRe >1560でLT^-1は急激に減少するという様に傾向に違いが見られる．レイノルズ数に依存した乱れの発達過程の違いについてはこちら⁽¹⁰⁾に詳しいが，パフが直接減衰せずに(その後減衰するとしても)一度は増幅の挙動をしめすRe > 1600のライフタイムの逆数とレイノルズ数の関係を拡大して示したのが図12bである．図12bにおいて，得られた結果を直線近似しライフタイムが無限大となるレイノルズ数を求めると約2300になる．既に述べた分裂パフの発生について調べた結果(図11)と照らし合わせると，パフのライフタイムはRe = 2300程度で無限に達するがそれと同時に分裂を開始する事を示唆する⁽¹¹⁾. 従来の研究^(12)-(15)ではパフのライフタイムは指数関数的に減衰するという仮定の下で求められており，本研究の様に直接的に計測した例はない．図12の結果を従来の方法で解析し, 各々の結果と比較したのが図13⁽²⁾である．Faisstら⁽¹²⁾ やHofら⁽¹⁴⁾はパフのライフタイムは有限のレイノルズ数で発散しないとし, Peixinhoら⁽¹³⁾とWillisら⁽¹⁵⁾は有限のレイノルズ数で発散するとした. 筆者らが直接測定した結果ではライフタイムは有限のレイノルズ数で発散する(図12b)が，パフの減衰を指数関数で近似するという従来の手法では発散しない(図13)という正反対の結論が得られた．この事実はライフタイムを指数関数で近似する解析法には検討の余地がある事を示している.

　 この様な低レイノルズ数領域の円管流遷移に関する最近の研究例は他にも挙げられ，Faisstら⁽¹⁶⁾やWedinら⁽¹⁷⁾は数値計算で管壁近くにトラベリングウェーブと呼ばれる周期的なストリーク構造が見られる事を示し，その後トラベリングウェーブは可視化実験⁽¹⁸⁾や数値計算等⁽¹⁹⁾で精力的に解析が進められている．これらの研究は流体力学における基本問題の一つ，円管流遷移に隠されたダイナミックな物理現象を不安定性解析によって記述する試みであり，非常に興味深く且つチャレンジングなテーマの一つである．

 

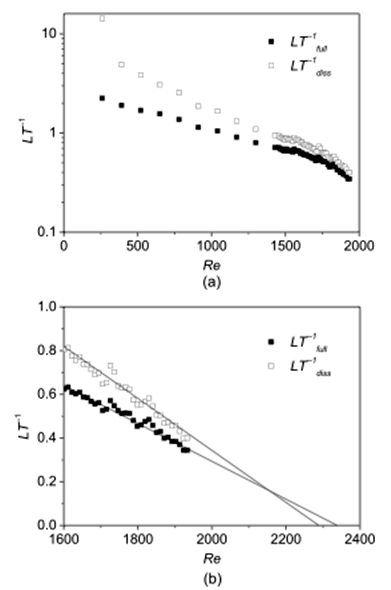
図12　レイノルズ数に対するライフタイムの逆数の変化⁽¹⁰⁾
(a) 250 < Re < 1900, (b) Re > 1600

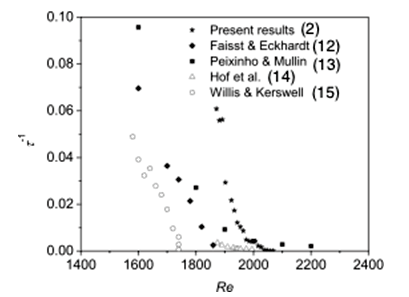
図13　これまでに報告されているライフタイムの逆数のレイノルズ数依存性⁽²⁾

 

５．おわりに

　レイノルズの発表から125年以上経過した現在も, 円管流の遷移現象は全容解明どころかそのアウトラインすら描けてはいない．筆者らはこれまでにそうした状況の打破を目指し，微力ながら円管流遷移の理解の一助となる研究成果を公表して来たつもりである. アイザック・ニュートンの言葉に「自然は単純である. だが単純すぎはしない. 」というのがある. 円管流の遷移はあまりにも日常的で単純な現象の様に見えるが実はそうではない事が本稿でお伝え出来ただろうか. 今後も引き続いて研究者が互いに協力し, 現象を曇り無き眼で見つめ絶え間無い努力を惜しまなければ，複雑に見える円管内遷移現象も比較的単純な物理的解釈に基づいて理解できる様になると筆者は信じている.

 

謝辞

　本稿でご紹介した博士課程の研究を遂行するにあたり常に叱咤激励して下さったFranz Durst教授と重要な参考意見を与え意義深い議論を交わして頂いたÖzgür Ertunç, Bülent Ünsal両博士に厚くお礼を申し上げる. またこちらへの寄稿の機会を与えて下さった日本機械学会流体工学部門広報委員会ニュースレター担当委員の塚原隆裕博士, 木上洋一准教授, 帆足英二氏に謝意を表する.

参考文献

(1)	西美奈, ドイツ留学日記, 日本機械学会熱工学部門TED Newsletter, No. 51, (2007), http://www.jsme.or.jp/ted/NL51/Nishi.pdf.
(2)	Nishi, M., Laminar to turbulent transition in pipe flow through puffs and　slugs, Doctor thesis, SVH, (2009), ISBN 978-3-8381-0318-1.
(3)	Reynolds, O., An experimental investigation of the circumstances which determine whether the motion of water shall be direct of sinuous, and the law of resistance in parallel channels. Philos. Trans. R. Soc. London, Ser. A 174, (1883), 935-982.
(4)	Pfenninger, W., In boundary layer suction experiments with laminar flow at high Reynolds numbers in the inlet length of a tube by various suction methods, in Boundary Layer and Flow Control, ed. by G. V. Lachman, Pergamon Press, Oxford, (1961), pp. 961-980
(5)	Nishi, M., Unsal B., Durst F. and Biswas, G., Laminar-to-turbulent transition of pipe flow through slugs and puffs, J. Fluid Mech., Vol. 614, (2008), 425-446.
(6)	Hof, B., Juel, A. and Mullin, T., Scaling of the turbulence transition threshold in a pipe. Phys. Rev. Lett. 91-244502 (2003), 1-4.
(7)	Trefethen, L., Chapman, S., Henningson, D., Meseguer, A., Mullin, T. and Nieuwstadt, F., Threshold amplitudes for transition to turbulence in a pipe, http://xxx.uni-augsburg.de/abs/physics/0007092.
(8)	Wygnanski, I. J. and Champagne, F. H., On transition in a pipe. Part 1. The origin of puffs and slugs and the flow in a turbulent slug. J. Fluid Mech. 59, (1973), 281-351.
(9)	Willis, A. P. and Kerswell, R. R., Turbulent dynamics of pipe flow captures in a reduced model: puff relaminarization and localized ‘edge’ states, J. Fluid Mech., Vol. 619, (2009), 213-233.
(10)	Nishi, M., Ertunc O. and Delado, A., Connection between full-lifetime and breakdown of puffs in transitional pipe flows, Seventh IUTAM Symposium on Laminar-Turbulent Transition, Springer, (2009), ISBN 978-90-481-3722-0, pp. 537-540.
(11)	Nishi, M., Ertunc O. and Delado, A., Direct measurement of lifetime of transitional structures in low Reynolds number pipe flows, Proc. 6th Int. Symp. on Turbulence and Shear Flow Phenomena, (2009).
(12)	Faisst, H. and Eckhardt, B., Sensitive dependence on initial conditions in transition to turbulence in pipe flow. J. Fluid Mech. 504, (2004), 343-352.
(13)	Peixinho, J. and Mullin, T., Decay of turbulence in pipe flow. Phys. Rev. Lett. 96-094501, (2006), 1-4.
(14)	Hof, B., Westerweel, J., Schneider, T. M. and Eckhardt, B., Finite lifetime of turbulence in shear flows. Nature 443, (2006), 59-62.
(15)	Willis, A. P. and Kerswell, R. R., Critical behavior in the relaminarization of localized turbulence in pipe flow. Phys. Rev. Lett. 98-014501, (2007), 1-4.
(16)	Faisst, H. & Eckhardt, B., Traveling waves in pipe flow. Phys. Rev. Lett. 91-224502, (2003), 1-4.
(17)	Wedin, H. & Kerswell, R. R., Exact coherent structures in pipe flow: traveling wave solutions. J. Fluid Mech. 504, (2004), 333-371.
(18)	Hof, B., van Doorne, C. W. H., Westerweel, J. & Nieuwstadt, F. T. M., Turbulence regeneration in pipe flow at moderate Reynolds number. Phys. Rev. Lett. 95-214502, (2005), 1-4.
(19)	Willis, A. P. & Kerswell, R. R., Coherent structures in localized and global turbulence in pipe flow. Phys. Rev. Lett. 100-124501, (2008), 1-4.