流れ　2010年4月号　目次

―　特集テーマ： 乱流遷移に携わる若手の研究紹介　― 亜臨界乱流遷移の理論的記述について 河原 源太（大阪大学） 実験的研究：主流乱れによる境界層の遷移過程について 松原 雅春（信州大学） 数値解析による研究：航空機の翼から発生する空力音と境界層不安定 跡部 隆（JAXA） 自由液膜内対流とその遷移過程 上野 一郎（東京理科大学） ヨーロッパでレイノルズの軌跡をたどる：円管内流れの遷移に関する研究 西 美奈（東京大学） 編集後記 編集後記（木上，帆足，塚原） 　｜　リンク一覧にもどる　｜

 

実験的研究：主流乱れによる境界層の遷移過程について

松原雅春 信州大学 高市皓太 信州大学 剱地利昭 岐阜工業高等専門学校

１．はじめに

　境界層が層流から乱流へ遷移する位置は熱輸送や摩擦抗力にも関係するため，例えば低圧ガスタービン翼の冷却問題などで工学上重要となる場合がある．軸流タービンでは燃焼器のすぐ下流の翼は高温にさらされるため前縁に冷却用の孔が設けられているが，前縁の次に高温にさらされる位置は乱流遷移位置の直後である．この位置に的確な冷却をすることがガスタービン全体の効率に対し重要であるが，乱流遷移の予測法が確立していないため設計が経験的な手法にゆだねられているのが現状である．

　乱流遷移についての研究は，撹乱に対する層流流れの安定性を理論的な基礎としてきた．乱流遷移を伴う流れ場では初期撹乱が十分小さいと仮定できる場合が多く，その仮定に基づいた線形安定性理論は，例えば気体中に放出された円筒状の液体が崩壊し，液滴に分裂するレイリー不安定性などをよく説明している．当然，線形安定性理論は境界層における乱流への遷移にも適用され，その一例として凹面境界層におけるゲルラー渦と呼ばれる縦渦の発生とその乱流への崩壊がある．凹面境界層に比べ平板境界層は安定した流れ場であるため，支配的な撹乱を容易に決定できず，線形安定性理論に基づく直接的な遷移予測は成功していない．凹面境界層の成功例は，流れが本質的に不安定で，一次不安定撹乱を容易に決められるためである．ここでは，平板境界層の乱流遷移のうち，主流乱れを撹乱源とした実験的な研究について紹介し，さらに筆者らが観察したいくつかの遷移過程について説明する．

２．主流乱れによる境界層遷移に関する実験的研究

　境界層遷移の実験的研究は歴史的に非常に長いことは，代表的な論文のひとつであるSchubauer and Skramstad ⁽¹⁾の実験が戦前に行われていることからもわかる．彼らは，線形安定性理論の解で流れ方向に波数を持つ二次元撹乱であるTollmien-Schlichting 波 (T-S 波) を確認するため，主流乱れを極限的に抑えた状態の実験を行った．その結果，T-S波の周波数帯の流速変動を観察し，間接的ながらその存在が示唆された．さらに，人工的な二次元撹乱を境界層内に導入して，そのときの撹乱を理論と比較・検証し，境界層内でT-S 波の成長を確認した．

　主流乱れによる遷移に関するKlebanoff⁽²⁾の先駆的な研究は，残念ながらKendal の論文⁽³⁾から間接的にしか内容を紹介できない．彼は整流部に乱流格子としてロープを張ることにより主流乱れ強さ0.3%を実現して，境界層を熱線流速計により調べた．T-S 波の存在については間接的な証拠しか得られなかった一方，スパン方向に波数を持った別の撹乱が存在することを発見している．この撹乱は後に，Klebanoff モードと呼ばれている．Kendall ⁽⁴⁾は流れの可視化と熱線計測から，整流部に挿入した乱流格子で発生した1%以下の主流乱れで，局所的に現れるT-S 波を観察している．撹乱振幅の成長曲線は線形理論によるT-S 波の成長とは一致しないものの，T-S 波が現れた流れ方向位置は理論と整合している． さらに，局所的に発生したT-S 波が，下流に行くにしたがい波数を増加させること，スパン方向の広がり方がGaster⁽⁵⁾の理論による見積りより小さいことも明らかにしている．Arnal et al. ⁽⁶⁾ や Kosorygin et al. ⁽⁷⁾ も測定した流速変動がT-S 波の周波数帯と一致し，間接的ではあるがT-S 波の存在を確認している．Kenchi et al. ⁽⁸⁾ はビデオカメラによる流れの可視化で，局所的に発生したT-S 波がΛ 形が並んだ構造に変形し，その後崩壊して乱流斑点が発生することを明らかにした．さらに局所T-S 波の発生位置や T-S 波周波帯で帯域フィルターをかけた流速変動の壁垂直分布が，線形理論と一致していることを見いだしている．

　1%以上の高い主流乱れの場合の実験⁽⁹⁾では，スパン方向に波数を持つストリーク構造が発生し，それが横方向の振動とともに乱流へ崩壊し，乱流斑点が発生することが突止められている．このストリーク撹乱のエネルギー成長率は主流乱れ強さの2 乗に比例していることがFranssson et al. ⁽¹⁰⁾によって明らかになっている．ストリーク撹乱の成長は直接数値シミュレーション（DNS） ⁽¹¹⁾でも観測されており， non-modal 成長理論^{(12) (13)} でもよく説明されている．また，Mans et al. ⁽¹⁴⁾は水槽での遷移過程の観察を行い，ストリークの波状崩壊を詳細に調べている．乱れ強さが低い場合でも，ストリークと思われる撹乱は観察されていたが⁽⁴⁾，当時においては層流乱流遷移に対するその役割は明確ではなかった．

 

３．平板境界層における遷移過程の観察

　主流乱れによる境界層遷移過程を明らかにするために，様々な乱流格子での乱流遷移の様子をアルコールミストによる流れの可視化で観察した．アルコールミストは壁面から境界層内に静かに流し込まれ，乱流格子がない場合はこのミストは鏡面上のきれいな膜となることを確認している．

　一辺が6 mm の角柱を30 mm 間隔で並べた乱流格子の場合の境界層遷移の様子を図1 に示す．主流流速 U_∞ = 7 m/s で左から右に流れている．前縁上での主流乱れ強さTu = u_rms/U_∞ = 3.5 % である．上側の中央と下側の中央に2 個の矢尻形の乱流斑点があり，また主流方向と平行のストリークが局所的に波状の撹乱を伴っているのが観察される．このストリークの崩壊過程の連続写真を図2 に示す． コントラストの強いストリークが白く写っている．これは壁付近の流れによってミストが集まっているためで，低速領域に相当することがPIV 計測から明らかとなっている⁽¹⁵⁾．このストリークが波状の運動を始める．これはストリークの低速領域と周りの高速の流れとの間で発生する変曲点型不安定性と考えられる．この波状の運動の後，ストリークは崩壊して局所的な乱流塊となる．この乱流塊がスパン方向と流れ方向に広がり，矢尻形の乱流斑点となる．このようなストリークによる遷移過程は過去の可視化実験^{(8) (9)}でも観察されており，比較的高い主流乱れの場合に見られる遷移過程といえる．

 

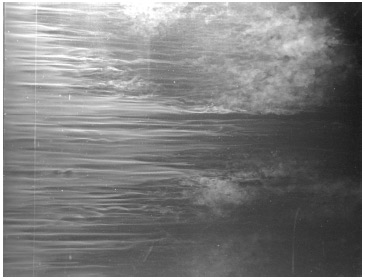
Fig. 1 Flow visualization of the boundary layer transition with Grid A
at U_∞ = 7 m/s. Range of the photograph is in 1.1×10⁵ ≤ Re_x ≤ 2.7× 10⁵.

 

Fig. 2 Sequence of a streak breakdown in the Grid A case,
at U_∞ = 4 m/s. Interval of sequence is 1/120 s.

 

　次に乱流格子をノズル入口上流に挿入した場合の境界層遷移の様子を図3 に示す．乱流格子として直径が 13 mm の円管を120 mm 間隔で並べており，各格子の中央の位置に直径2 mm の孔が上流に向かってあいている．円管内を圧縮機で加圧することにより上流に噴流を吹かせ，乱れ強さを連続的に変化できるようになっている．図3 では主流流速U_∞ = 12 m/s，前縁上での主流乱れ強さTu = 0.33% である．下流に乱流斑点が認められるが，上流では図1 で見られたストリークは観察されず，そのかわり特徴的な三次元構造を持つ局所的な撹乱がいくつかみられる．この三次元構造の崩壊過程を図4 に示す．一番上の写真では撹乱はほとんど見えないが，次の写真では局所的な濃淡が流れ方向に並んでいるのがわかる．これが次の写真ではΛ型の構造が流れ方向に並んでおり，その後すぐに乱流へと崩壊している．この場合も崩壊のあと乱流斑点が形成されている．長時間のビデオ画像の観察では，流れ方向の濃淡が見えたのちΛ 型の構造が千鳥状に見られることもあった．同じ乱流格子を使った場合の熱線計測⁽⁸⁾でも，T-S 波の周波数帯域の撹乱を確認しており，さらに発生した位置が下流側の中立安定曲線付近であることを確かめている．初期の撹乱構造が流れ方向に波数を持つこと，その後Λ 構造が流れ方向または千鳥状に並ぶことを考え合わせると，この撹乱は局所的に発生したT-S 波と考えられる．

 

Fig. 3 Flow visualization of boundary layer transition with Grid C
at U_∞ = 12 m/s. Range of photograph is in 2.6×10⁵ ≤ Re_x ≤ 6.6×10⁵.

 

Fig. 4 Sequence of a T-S wave breakdown in the Grid C case,
at U_∞ = 12 m/s. Interval of sequence is 1/120 s.

 

　図5 はさらに主流乱れが小さい場合の連続写真である．乱流格子は前述のノズル上流においたもので，上流への噴流は止めている．主流流速はU_∞ = 12 m/s，乱れ強さはTu = 0.19% である．局所T-S 波の崩壊過程も観察されたが，連続写真のようにストリーク構造に細かい波状の二次不安定が現れ崩壊していく過程も観察された．さらに，図6 に示すように，高速領域と思われる黒く写っているストリークの両側に発生する二次不安定による崩壊も観察された．T-S 波のような modal な撹乱は指数関数的に成長するため，代数的な成長をするnon-modal な撹乱に比べ初期撹乱が小さい場合には有利であると考えられている．Tu=0.19% の結果はこのことと矛盾している．また図5 と図6 のどちらのストリークも乱れ強さが大きい場合のストリークに比べ流れ方向の長さが比較的短い．これは，この短いストリークの崩壊過程が3 番目の過程として分類できる可能性を示唆している．

 

Fig. 5 Sequence of a wavy breakdown of streak in the Grid C case without jet blowing,
at U_∞ = 12 m/s. Interval of sequence is 1/120 s.

 

Fig. 6 Sequence of a symmetrical (varicose) breakdown of streak in the Grid C case
without jet blowing, at U_∞ = 12 m/s. Interval of sequence is 1/120 s.

 

４．まとめ

　以上のように，主流乱れを受ける平板境界層においては遷移過程は一通りではなく，少なくともストリークによるものと局所T-S 波による二つの過程が存在する．さらに非常に弱い主流乱れの場合，別の過程の存在も示唆されている．主流乱れのどの撹乱成分が各過程の撹乱を発生させているかについても，ほとんど研究されていないといえる．工学的な設計に役立つような遷移位置の予測法の確立には，我々に残された課題は多いと言わざるを得ない．

 

参考文献

(1)	Schubauer, G. B. and Skramstad, H. K., Laminar boundary layer oscillations and the transition on a flat plate, Journal of Aerospase Science, (1947), vol. 14, pp. 69-78.
(2)	Klebanoff, P. S., Effect of Free Stream Turbulence on the Laminar Boundary Layer, Bulletin of American Physical Society, Vol. 10, No. 11, (1971), p. 1323.
(3)	Kendall, J. M., Experiments on Boundary-Layer Receptivity to Freestream Turbulence, AIAA paper 98-0530, (1998).
(4)	Kendall, J. M., Experimental Study of Disturbances Produced in a Pre-Transitional Laminar Boundary Layer by Week Freestream Turbulence, AIAA paper 85-1695, (1985).
(5)	Gaster, M. and Grant, I., An Experimental Investigation of the Formation and Development of a Wave Packet in a Laminar Boundary Layer, Proceedings of the Royal Society of London. Series A, Vol. 347, (1975), pp. 253- 269.
(6)	Arnal, D. and Juillen, J. C., Contribution Experimentale a L’etude de la Receptivite D’une Couche Limite Laminaire, a la Turbulence de L’ecoulement General, Rapport Technique, 1/5018, (1978), ONERA.
(7)	Kosorygin, V. S. and Polyakov, N. Ph., Laminar Boundary Layers in Turbulent Flows, In Laminar- Turbulent Transition (ed. D. Arnal and R. Michel), (1990), pp. 573-578, Springer.
(8)	Kenchi, T., Matsubara, M. and Ikeda, T., Laminar Turbulent Transition in a Boundary Layer Subjected to Weak Free Stream Turbulence, Journal of Fluid Science and Technology, Vol. 3, (2008), No. 1, pp. 56-67.
(9)	Matsubara, M. and Alfredsson, P. H., Disturbance Growth in Boundary Layers Subjected to Free-Stream Turbulence, Journal of Fluid Mechanics, Vol. 430, (2001), pp. 149- 168.
(10)	Fransson, J. H. M., Matsubara, M. and Alfredsson, P. H., Transition Induced by Free-Stream Turbulence, Journal of Fluid Mechanics, Vol. 527, (2005), pp. 1-25.
(11)	Jacobs, R. G. and Durbin, P. A., Simulations of Bypass Transition, Journal of Fluid Mechanics, Vol. 428, (2001), pp. 185-212.
(12)	Luchini, P., Reynolds-Number-Independent Instability of the Boundary Layer Over a Flat Surface: Optimal Perturbations, Journal of Fluid Mechanics, Vol. 404, (2000), pp. 289-309.
(13)	Andersson, P., Berggren, M. and Henningson, D. S., Optimal Disturbances and Bypass Transition in Boundary Layers, Physics of Fluids, Vol. 11, No. 1, (1999), pp. 134- 150.
(14)	Mans, J., de Lange, H. C. and van Steenhoven, A. A., Sinuous breakdown in a flat plate boundary layer exposed to free-stream turbulence, Physics of Fluids, Vol. 19, 088101, (2007), (4 pages).
(15)	Alfredsson, P. H. and Matsubara, M., Free-stream turbulence, streaky structures and transition in boundary layer flows, AIAA-paper, 2000-2534, (2000) (9 pages).