流れ 2010年4月号 目次
― 特集テーマ: 乱流遷移に携わる若手の研究紹介 ―
| リンク一覧にもどる | |
数値解析による研究:航空機の翼から発生する空力音と境界層不安定
跡部隆
池田友明
|
1.翼周り流れから発生する騒音
近年の環境意識の向上に伴い,航空機の低騒音化は低CO2化と並ぶ重要な課題となってきている.特に離着陸時においては,エンジン騒音を含む騒音全体の中で,翼や高揚力装置・脚などに起因するいわゆる空力騒音の比重が大きくなる.これら物体周り流れから発生する空力音は,主に流れにおける渦の発生やその非定常変動に起因するため渦音と呼ばれる(1).これは,渦同士の相互作用や物体近傍の剪断層を渦が移流する際に生じる変動を音源として微小圧力波が放射され,それが音源近傍に存在する物体表面で散乱される現象である.この時,物体の長さスケールが音波に比べて十分小さい場合(即ち,音響的にコンパクトである場合)や,翼後縁のように狭端を持つ場合には,放射音は非常に大きく増幅される.特に周期的な渦変動がそれらの物体近傍に存在する場合には,卓越した狭帯域騒音として認識される.風の強い日に電線やベランダの手摺りなどから出る風切り音はその典型的な例である.
筆者らはこのうち翼後縁から発生するトレーリング・エッジ(TE)ノイズと呼ばれる空力音を対象として,境界層の不安定性の観点から騒音発生メカニズムの解明に取り組んできた.TEノイズは翼の後縁から散乱される空力音で,後縁から周期的な渦放出を伴う場合,前述のように音響スペクトルに狭帯域のピークを持ち,その周波数は主流速度の1.5乗の依存性を持つことが理論及び風洞実験を通して確かめられている(2)-(4).近年,計算機性能の飛躍的な向上と数値計算技術の発展により,実験のみならず数値シミュレーションを用いても翼周り流れとそれに付随するTEノイズの発生を詳細に再現可能となってきている.これら実験研究及び数値計算を通して,空力音の発生源となる後縁からの周期的な渦放出は,より上流での翼面境界層と密接な関わりをもつ,いわゆる音響フィードバックによって引き起こされることが分かってきた.即ち,後縁から放射された音響変動は上流側に伝播しつつ翼面境界層に受容され,そこで不安定波を励起する.不安定波は下流に伝播しながら成長し,再度音源となる下流での渦放出を引き起こす,一種のフィードバックループを形成していると説明される(5)-(8).特に非定常数値シミュレーションは境界層遷移の捕獲などと共にTEノイズ発生メカニズムの理解に大きく貢献している.
この音響フィードバックループは,上流側の境界層の状態に大きく影響を受けることがわかっている.境界層が後縁の手前で十分乱流に遷移してしまうと,後縁で周期的な渦放出は再現されず,狭帯域騒音も発生しない.このため少なくとも翼の片面は層流である必要があり,さらに特定の周波数の速度変動が不安定波として成長する速度分布が層流側の境界層内で実現されなくてはならない.実際,風洞実験においてもわずかな実験条件の違いでフィードバックループが形成されたりされなかったりで,TEノイズの再現に苦労することが多々あるようである.
2.低Re数での音響フィードバックループ
上述の音響フィードバックの説明はRe数がある程度大きく(翼弦長と一様流速度に関して数十万のオーダー),境界層遷移を伴う場合を想定している.これは元来実験で再現されるTEノイズがそのRe数の範囲であるためだと考えられ,これをサポートする実験研究が多く存在する.一方,境界層遷移を伴わない低Re数(数千~数万程度)においても翼後流では非定常渦変動が発生し,同様にTEノイズが観測されるはずである.この範囲のRe数を実験で再現しようとすると,コード長及び流入速度は十分小さく取る必要があり,結果的に発生する音圧は非常に小さいため騒音として認識されるレベルにはなり得ない.しかしながら,音響フィードバックループの低Re数での実現性を考察することは,空力音発生のメカニズムに関して理解を深める上でも重要である.本節では低Re数での翼周り流れから発生する空力音に関して,最近の筆者らの研究成果を簡単に紹介したい.
ここでは,マッハ数M=0.3の一様流中に置かれた迎角3.5度のNACA0006翼から発生する圧力変動(=音波)を高精度スキームを用いて数値的に直接解析する.計算は二次元圧縮性Navier-Stokes 方程式を支配方程式とし,流れ場はC型格子を用いて差分法により離散化する.移流項・粘性項とも空間6次精度のコンパクト差分スキームにより中心差分で評価する.時間進行には4次精度のRunge-Kutta法を用いる.計算手法の詳細は参考文献(9)を参照されたい.Re数は20,000であり,従来の空力騒音に関する研究より一桁小さい流れ場を解いている.

図1 NACA0006二次元翼まわりの圧力変動.

図2 音響フィードバックループが形成されたときの圧力変動.
上述の手法を用いて得られた計算結果は,計算初期では音響フィードバックループは形成されず,翼後流では後流剪断層の不安定から決定された自励振動周波数を持つカルマン渦列が発達する(図1).ここでは境界層内の変動はごく弱く,後縁から後方にて速度変動は急激に発達する.しかしながら,さらに計算を続けると次第に上面側の境界層変動が卓越し,カルマン渦放出周波数が低下する(図2).それに伴い,TEノイズの周波数も低下し,発生する音圧レベルはおよそ一桁増大する.流れ計算から得られた速度分布に対してOrr-Sommerfeld方程式に基づいた線形安定性解析を適用することで,この図2で再現されるノイズの周波数は境界層不安定の周波数と一致することも確認される.この図1から図2への遷移課程には音響フィードバックループが介在すると考えると容易に説明がつく.さらに補足すると,同じ流れにおいて流入マッハ数がより小さい場合にはこの遷移は起こらず,図1のような後流不安定が支配的な流れが得られるのみである.マッハ数の上昇に伴い音響変動も増大するため,受容される不安定波も増幅され,境界層不安定がより顕著な流れが引き起こされるものと考えられる.
興味深いのは,この音響フィードバックがループを形成する(=ONになる)と,周波数が低下し,さらに音圧変動が増大するため,翼表面にトータルで作用する力の時間変動が卓越することである.筆者らの計算例の中には,フィードバックループがONになることで,揚力の変動幅が全体の数十%にもなるケースもあった.例えば図3で示した揚力の時間変動履歴は,Re数を変化させることでフィードバックループのONとOFFが入れ替わる様子を再現したものである.低Re数流れの場合,一般に境界層が層流であるため剥離しやすく高Re数の場合と比べて翼の性能が低下することが知られているが,それに加えて音響フィードバックの影響により境界層に大きなスケールでの低周波変動が励起され,空力特性が非定常に大きく変動し得ることを示唆している(10).
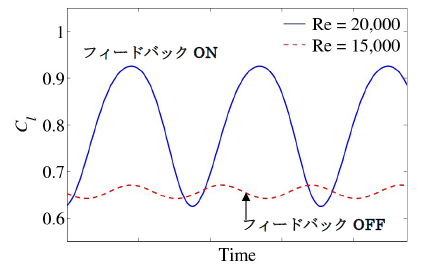
図3 NACA0006二次元翼の揚力の時間変動(M=0.1, 迎角4度).
3.まとめ
本稿では航空機の翼後縁から発生する空力音について,境界層の安定性という観点からその発生機構のキー・ファクターともいえる音響フィードバックループについて議論した.高精度な非定常圧縮性計算による低Re数流れの空力解析と線形安定性解析から,境界層の安定性は音響フィードバックループのON/OFFに直接的な関わりをもち,一度このループがONになると発生する空力音が飛躍的に増大する.さらに副次的な結果として,低Re数における翼周り流れでは揚力などの空力特性に無視できない影響を及ぼし得ることを示した.
ただ実環境ではこのような有限のマッハ数での低Re数流れは想定し難い.しかしながら,例えば,現在JAXAが中心になって進めている火星複合探査計画(MELOS)では,火星大気内に航空機型探査機を投入し飛行探査させるミッションが候補の一つに上がっている.火星大気の密度は地球のおよそ100分の1であるため,大型の模型飛行機程度の探査機を亜音速で飛ばすことを想定した場合,翼面境界層は層流であると考えられる程度に十分Re数は小さい(数千~数万程度).極端な例であるが,このような環境下では上述のように空力特性の非定常性が重要な問題になるものと考えられる.
参考文献



