流れ 2010年4月号 目次
― 特集テーマ: 乱流遷移に携わる若手の研究紹介 ―
| リンク一覧にもどる | |
自由液膜内対流とその遷移過程
上野 一郎 |
誰しも一度はシャボン玉で遊んだ記憶はあると思う.針金などを曲げてリング状にしたものに石鹸水などの膜を張り,息を吹きかけて膨らませる(図1).シャボン玉を作るにあたって,地上では重力の影響があるため,界面活性剤等で表面張力を弱めた上で,液体とリングとの濡れ性で液膜を保持することが重要となる.大きなシャボン玉を作るために,石鹸水を作る際にオリジナルのレシピを持っていた方も多くいたのではないだろうか.

Fig. 1 The Soap Bubbles (Les Bulles de savon) (Edouard Manet, 1867), Musee Calouste Gulbenkian, Lisbonne.
では宇宙などに行って,重力が小さい状態ではどうなるか.アメリカの宇宙飛行士であるDonald Pettit博士は,2003年に当時建設中であった国際宇宙ステーションに滞在した際にSaturday Morning Science(1)と題して様々な科学的デモンストレーションを行った.その中に,直径15 cmほどのリングを用いて,通常の飲料水の膜をリング内に形成し,ミルクを垂らしてそっと混ぜることでパイこね変換を模擬したり,インクと注射器を使ってドラゴンの絵を液膜上に描いたりというデモンストレーションがある.重力の影響が小さい場合には,特別なレシピを持ち出すまでもなく,周囲だけを保持した状態の薄い液膜,すなわち「自由液膜」を形成することが出来るようになる.さらに,Pettit博士は,自由液膜を保持しているリング近くに半田ごてを近づけることで,液膜内に「2次元的」な対流を実現している(図2).この場合,厚み方向に均一に,すなわち,2次元的な対流場が励起されている.今回この記事では,2つの自由表面を有する液膜,自由液膜中でどのような対流場が発生するのか,またそれら対流場がどのような遷移過程を呈するのか,ということに焦点を当てて紹介したい.

Fig. 2 Flow in a free liquid film of water induced by placing a soldering iron near the wire holding the film (captured from a DVD of ‘Saturday Morning Science’ delivered from Dr. Donald Pettit. (c) NASA).
本記事では,流体の駆動力として特に表面張力差を考える.表面張力σ は一般に濃度c,かつ,または,温度Tに依存する.したがって表面張力 σ = σ(c, T)の全微分により,
![]()
と表され,それぞれ表面張力の濃度係数および温度係数が0でない場合において,自由表面上に表面張力差が生起する.この表面張力差により表面上の流体が駆動され,さらに粘性剪断によって周囲流体に対流が及ぶ.このような対流は,この現象を紹介(2)したイタリアの物理学者の名前を取ってマランゴニ(Marangoni)対流と呼ばれる.ちなみに,濃度差マランゴニ対流として広く知られているものに,『ワインの涙』と呼ばれる現象(図3)がある.一般には,濃度係数,温度係数ともに負の値を有することが知られており,したがって一般的には,自由表面上において高濃度領域から低濃度領域へ,あるいは高温領域から低温領域に向かってマランゴニ対流が生起する.図3で示した『ワインの涙』では,ワイングラス壁面上のメニスカス付近でアルコール成分が先に蒸発することによりアルコール濃度が下がり,ワインのバルク表面と濃度差が生じることになる(3,4).

Fig. 3 ‘Tears of wine.’ Solutocapillary effect drives the wine climbing up the glass wall against the gravity. Rayleigh-Taylor-like instability arises when an amount of wine on the wall reaches beyond a threshold to keep the wine heavier than the ambient gas climbed up on the wall.
さて,ここでは特に,表面張力の温度依存性を利用した対流場に着目して現象を紹介していく.すなわち,温度差マランゴニ対流として知られている現象である.解析対象を図4に示す.温度差を規定するため,丸形ではなく矩形の自由液膜を想定している.一方を加熱,一方を冷却して温度差DTを両端壁間に実現した矩形孔に液体を保持している.液膜上下に自由表面が存在し,表面は温度勾配方向と平行となる.液膜の形状は2つのアスペクト比Γx = Lz/Lx, Γy = Lx/dを用いて決定する.なお,当該系における温度差マランゴニ効果の強さを表す指標として,次のように定義するマランゴニ数Ma = σT(ΔT/ Lx)d2/(ρνk)を導入する.
![]()
ここで,σT:表面張力温度係数 (= |∂σ/∂T|),ΔT:高温壁・低温壁間温度差,ρ:密度,ν:動粘度,κ:温度拡散率である.
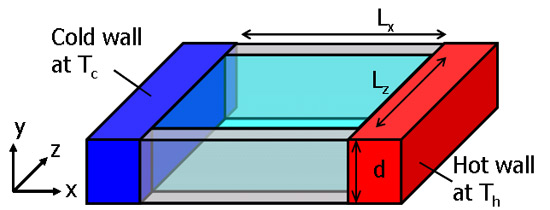
Fig. 4 Target geometry; a free liquid film sustained in a rectangular hole of d in thickness.
変形を起こさない直方体液膜を対象とし,連続の式・N-S方程式・エネルギー方程式を支配方程式とする3次元数値解析の結果を以下に示す.自由表面上では力学的境界条件としてマランゴニ境界条件を,また熱的境界条件として断熱条件を課している.まず,マランゴニ効果が非常に弱い場合,すなわち,両端壁間温度差が小さい場合には,液膜厚さ方向に2層構造を伴う2次元定常流が液膜内に発生する.液膜のスパン方向中央部での断面図を図5に示す.ここで,比較のため,底面が固体壁の場合(1自由表面を有する液膜の場合)の定常流の断面図も併せて示している.自由液膜の場合には,上下自由表面において温度差マランゴニ効果が生起し,高温壁から低温壁に向かって対流が生じる.それぞれ低温壁にぶつかった流れは,液膜厚さ方向中央部において高温部に戻っていき,結果的に上下に2層構造を有する基本対流場が見られる.一方で,底面が固体壁面で自由表面が上部のみの液膜においては,自由表面においてやはり高温壁から低温壁に向かう流れ場が発生し,低温壁にぶつかった後に壁面沿いに高温壁へと向かっていく流れが基本対流場となる.

Fig. 5 Cross-sectional views of two-dimensional steady flow; (1) a free liquid film and (2) a liquid film in a cavity.
ここで,温度差を大きくしていくことで,温度差マランゴニ効果を強くしていくと,温度勾配に対して斜行するロール状構造が低温壁側から高温壁側へと伝播していく(図6).図中(1)の液膜上表面および(2)断面図においては,温度波を明確に示すために,温度の変動分を表記している.図に見られるように,周期的に発生する渦が,高温壁に向かって定常的に流れていく.このような不安定性は,Hydrothermal wave(以下HW)不安定と呼ばれ,1自由表面を有する薄液膜系において,1983年にSmith & Davis(5)によって線形安定性解析によって予測され,その後1998年にRiley & Neitzel(6)によって実験的にその存在が示されている.また,Kawamura et al.(7)によって液膜におけるHW不安定性と,両端を固定した円柱形液柱におけるそれとの比較が行われている.Smith & Davis (5)により,HW不安定性が発生した際の波の伝播角度 φHWおよび遷移条件となる臨界マランゴニ数Macが試験流体のプラントル数Prの関数として示されている.自由液膜におけるHW不安定においては,1自由表面を有する液膜と比較して,波の伝播角度が大きくなり,また波数が若干ではあるが大きくなる傾向が見られる.また,高温壁近傍での定在渦存在領域Lsvは1自由表面液膜での長さ(7)よりも短くなる.断面図を見ると,自由液膜においては,2層構造は維持されているが,上下層で位相をずらして渦が形成されており,基本対流場においては液膜厚さの半分の厚みを有していた層構造が,それぞれ液膜厚みの70 %近くの大きさの渦が周期的に形成している.このそれぞれの層構造の有効厚みの変化によって,HWの伝播角度および波数の変化として現れている.さらにマランゴニ数を大きくすると,それまでの2層構造は崩壊し,スパン方向に波数を有するセル状構造が励起する.
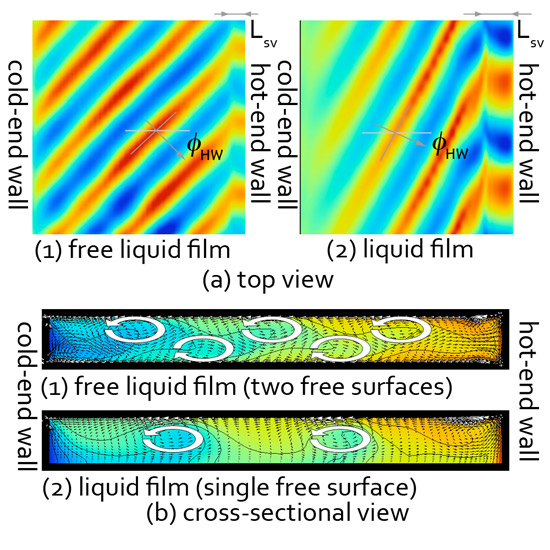
Fig. 6 Typical example of 'oscillatory' flow; (a) top view of the deviation of the temperature over the top free surface and (b) cross-sectional view in x-y plane in the cases of (1) free liquid film (two free surfaces) and (2) a thin liquid film in the cavity (a single free surface (top surface is free) under the same intensity of the thermocapillary effect. Right-hand side is the hot wall, and the opposite is the cold wall for each frame. Marangoni number Ma is kept constant at 1×103.
さて,数値計算によりこのようなHW不安定が実現することが示されたのを受け,実際に実験により自由液膜内対流の観察を試みる.地上では前述の通り,液膜形成に重力の影響を受けるため,ボンド数Bo = ρgd2/σが小さくなるような液膜を形成する必要がある.そこで著者らの研究グループでは,図7のような矩形孔を有する試験片を作製し,その孔内に表面張力および濡れ性により液膜を保持することにより自由液膜の実験を行った.ここでは,試験流体として動粘性係数5 cStのシリコーンオイル(Pr = 68.4 at 25 °C)(信越化学工業(株)製)を用いた.この流体の特徴として,物性が安定しており,また,表面張力の温度係数がほぼ一定(著者らの測定結果により,∂σ/∂T = -6.37×10-5 N/(m K))であることが挙げられる.

Fig. 7 Example of liquid film holder (right). Liquid film is formed in a square region indicated by an arrow. Thickness of the holder in the figure is of 0.2 mm.
以下に実験により得られた自由液膜内に生起する対流場を紹介する.液膜厚さd = 1.2 mmの場合における各種対流場の上方観察図を図8に,その中での代表的な粒子挙動に注目して再構築したものを図9に示す.各フレームとも右側が高温壁,左側が低温壁に相当する.透過光による上方からの観察のためわかりにくいが,顕微鏡を用いて被写界深度を浅くして観察を行い,焦点位置を液膜厚み方向に変えていくことで下記の結果を得ることが出来る.すなわち,温度差マランゴニ効果が小さい場合 (a), (b)においては,図5で示した数値計算での結果と同様,液膜厚さ方向に2層構造が存在し,上下それぞれの自由表面近傍において粒子は高温壁から低温壁へ,液膜厚さ方向中央部においては逆向きの流れが実現している.温度差マランゴニ効果が強くなるにつれ,2層構造のそれぞれ厚み方向中央部近傍においてスパン方向の速度成分が現れる(図中(c)).ここで粒子挙動,あるいはここでは割愛しているが放射温度計を用いた表面温度分布測定では自由表面近傍は(a), (b)と同様,2次元的な定常流の状態を維持している.さらに温度差マランゴニ効果を強くすると,自由表面近傍の粒子もスパン方向の速度成分を有し,また,表面温度も非定常な分布を示すようになる(図中(d)).したがって,このケースでは,液膜内対流場は2段階の遷移過程を経ることになる.ここで注意すべきは,数値計算で予測したような,ある一定の波数を有し,低温壁側から高温壁側へと伝播する温度波は出現しない.
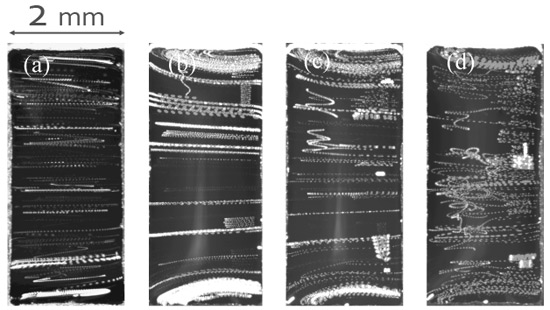
Fig. 8 Typical examples of the induced flow in the film of (Lx, Lz, d) = (2.0 mm, 4.0 mm, 1.2 mm) observed from above; right-hand side is hot wall, and left cold. (a) ΔT = 2.3 K (Ma = 3.1×102), (b) ΔT = 25.3 K (Ma = 3.5×103) , (c) ΔT = 40.1 K (Ma = 7.4×103) and (d) ΔT = 46.5 K (Ma = 9.2×103). Frame (a) obtained by integrating the frames for 3.0 s, (b) for 2.0 s, (c) & (d) for 0.5 s.
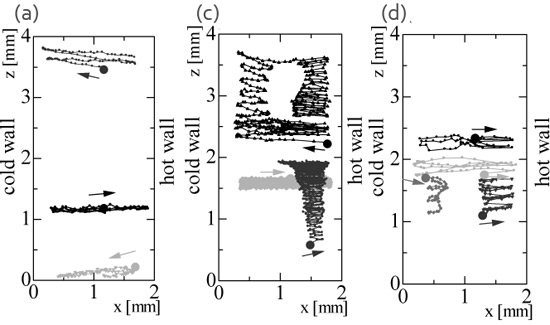
Fig. 9 Typical examples of the particle behavior in the film; particles are tracked from the results with the same index as shown in Fig. 8. Frames (a) indicate trajectories of selected particles tracked for 6.0 s, (c) for 7.0 s and (d) for 1.0 s.
このように,温度差マランゴニ効果を大きくしていくにつれ,自由液膜内では2つの遷移過程が生起する.2層構造内部でスパン方向運動が開始される遷移を第1遷移,その後,液膜全体で非定常流へと遷移する条件を第2遷移として,様々なアスペクト比の液膜に対してそれぞれ第1,第2臨界マランゴニ数Mac1,Mac2で表したもの(8)を図10に示す.アスペクト比Γxに対しては特定の傾向は現れないが,Γyに対しては異なる液膜厚さに対して両臨界値ともともに一定の傾向を示すこととなり,現象の予測が可能となる.
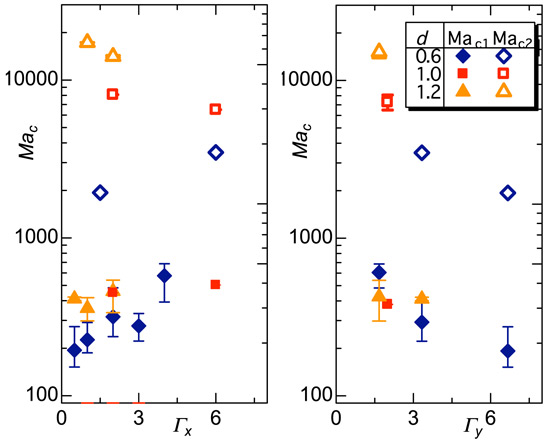
Fig. 10 Onsets of 1st and 2nd transitions of the flow inside free liquid film of d > 0.2 mm as functions of aspect ratio Γx (left) and Γy (right).
一方,液膜厚さがd = 0.2 mmの場合における各種対流場の上方観察図を図11に,その中での代表的な粒子挙動に注目して再構築したものを図12に示す.ここでも各フレームとも右側が高温壁,左側が低温壁に相当する.液膜が相対的に薄くなると,温度差マランゴニ効果が微弱であっても粘性に打ち勝ちながら液膜厚さ方向中央部を高温壁に向かって戻ることはもはや出来ず,流体は厚み方向に1層の構造を呈し,スパン方向にセル状の2対の渦を形成することになる(図中(a)).対流は液膜スパン方向中央部で高温壁側から低温壁側へと流れ,側壁近傍において高温壁へと戻っていく.温度差マランゴニ効果を大きくしていくと,次第に低温壁近傍でスパイラル構造を呈するようになり(図中(b)),その後,側壁近傍でもスパイラル構造が出現する.温度差マランゴニ効果によって生起する対流場の影響で,液膜の厚みが不均一となり,スパン方向中央部付近では極端に薄くなり,可視化用のトレーサ粒子(直径30 µm)がその領域に入り込めずに蛇行するようになる(図中(d)).

Fig. 11 Typical examples of the induced flow in the film of (Lx, Lz,, d) = (2.0 mm, 4.0 mm, 0.2 mm) observed from above; (a) δT = 0.6 K (Ma = 2), (b) δT = 3.1 K (Ma = 11), (c) δT = 5.5 K (Ma = 20), and (d) δT = 12.8 K (Ma = 48). Frames (a) is obtained by integrating the obtained frames for 2.0 s, (b) for 1.5 s, (c) & (d) for 1.0 s.
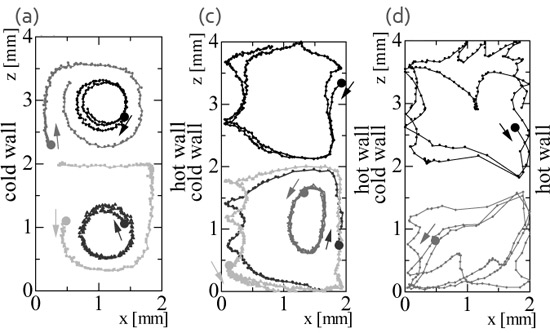
Fig. 12 Typical examples of the particle behavior in the film d = 0.2 mm; particles are tracked from the results with the same index as shown in Fig. 10. Frames (a) indicate trajectories of selected particles tracked for 10.0 s, (c) for 4.0 s, and (d) for 2.6 s.
いずれにせよ,実験においては底面が固体壁である1自由表面を有する液膜の場合と大きく異なり,一定の波数を有して低温壁から高温壁へと伝播するHW不安定性は出現しない.スパン方向を充分長く取った場合においても,スパン方向に1程度しか出現しない.1自由表面液膜あるいは数値計算で対象としている系と当該実験が大きく異なるのは,液膜の静的・動的な変形である.自由液膜の場合,周囲部のみで液膜を支えているため,液膜内対流によって生起する運動量の変化に伴う変形は不可避であり,より大きな因子として存在することになる.そこで,共焦点型レーザ変位計を用いてこのような対流場が生起している際の自由表面位置および液膜厚み分布の計測を行った例(9)を図13に示す.ここでは,前出の自由液膜とアスペクト比が異なることに注意する.図では上方より観察した流跡線,放射温度計を用いて測定した上方表面温度分布,さらに液膜スパン方向中央部における自由表面位置・膜厚分布を示している.著者らの研究グループでは,今後,液膜の静的・動的変形を考慮した自由液膜内対流遷移過程についてさらに研究を進める予定である.
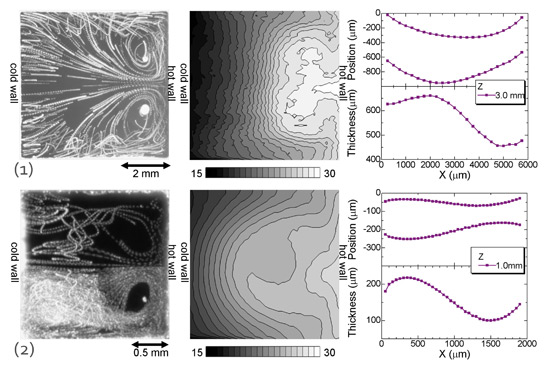
Fig. 13 Typical examples of the induced flow in the film of v/v0 = 1.0 in the volume ratio; the path line for 1.0 s (left), the top surface temperature (center) observed from above, and the positions of free surfaces and the thickness distribution along the center line of the film (right) in the case of (Lx, Lz, d) = (6.0, 6.0, 0.6) [mm] (top frames) and (2.0, 2.0, 0.2) [mm] (bottom) at ΔT = 15.0 [K].
ここで,地上で行った著者らの自由液膜内対流場(図8,9,11,12)と,国際宇宙ステーション上でのPettit博士による自由液膜内対流場(図2)に注目していただきたい.同様の温度勾配を付加しているにも関わらず,対流の向きが全く逆になっている.これまで,この差違については日本マイクログラビティ応用学会などで議論が重ねられてきており,Pettit博士の実験は試験流体の蒸発によるものであるというような意見が出てきている.著者らの研究グループでは,しかし,蒸発以外の大きな因子がこのような対流場の決定に関わっているであろうと考えており,近々報告の予定(9)である.
以上,温度差マランゴニ効果によって自由液膜内に出現するさまざまな対流場とその遷移過程についてざっと紹介してきた.閉領域内での対流遷移については,自然対流や強制対流など様々な系でこれまで数多くの研究が行われており,非常に歴史のある研究分野である.その中でも,今回は自由表面を有し,マランゴニ効果により自発的に対流が生起し,また対流によって自由表面の変形を伴う系として,自由液膜内対流にスポットを当てさせていただいた.このような系は,著者も共同研究者として参画して2008年夏より国際宇宙ステーション上で実施しているハーフゾーン液柱内マランゴニ対流に関する研究(10)も含め,材料生成や特殊環境での熱流体ハンドリング技術への応用が期待されるものである.拙稿により一人でも多くの方がこのような分野に関心を持っていただけると幸いである.
拙稿で紹介した著者らの研究グループによる成果は,著者が主宰する東京理科大学 理工学部 機械工学科 界面熱流体力学研究室の鳥居孝充氏(現:横河電機株式会社),渡辺俊貴氏,松谷敏宙氏,勝田健史氏,出来尾祐美氏によるものである.また,これらの研究の一部は,文部科学省私立大学学術研究高度化推進事業学術フロンティア推進事業 東京理科大学総合研究機構ホリスティック計算科学研究センター(1995~2010)より助成をいただいた.記して謝意を表する.最後に,拙稿をまとめる機会をいただいた塚原隆裕博士(東京理科大学)に心よりお礼申し上げる.
参考文献


