Newsletter  2022.11  Index

Theme : "Mechanical Engineering Congress, 2022 Japan (MECJ-22)” Preface Hideo MORI, Tetsuya KANAGAWA Wall Modelling for Engineering Turbulence CFD Kazuhiko SUGA (Osaka Metropolitan University) Prediction of the flow of granules Toshitsugu TANAKA (Osaka University) Design Optimization of Turbomachinery by Artificial Neural Networks as a Meta-model Daisaku SAKAGUCHI (Nagasaki University) Deep learning for viscoelastic fluids and turbulent diffusion Takahiro TSUKAHARA (Tokyo University of Science) Advanced fluid measurement using mode decomposition Taku NONOMURA (Tohoku University)

 

Prediction of the flow of granules

Toshitsugu TANAKA Osaka University

Abstract

Not only gases and liquids but also powders and granules “flow”. For example, sand in an hourglass flows, as shown in Fig. 1.  In the hourglass, the granules, which are an aggregate of solid particles, exhibit a solid, gas and liquid state and undergo a phase transition. The behavior of powders and granules alone is complex enough, but when they are coupled with the surrounding gas flow, they exhibits even more complicated behavior. For example, in a fluidized bed, the contained powder or granules are fluidized by the gas flow introduced from the bottom of the container, and bubbles form, as shown in Fig. 2.

Because of the diversity of powder and granules characteristics, such as size distribution, shape and adhesion, discrete particle simulations⁽¹⁾ are widely used, including in industrial applications. Discrete Element Method (DEM) ⁽²⁾, which uses a contact force model as shown in Fig. 3, is a typical one of this type of simulation methods, and can represent all three state observed in the hourglass.

When using DEM for simulating fluid-solid multiphase flows, there are two methods for simulating fluid flow from the viewpoint of resolution to the particle scale: one is a particle-resolved type, and the other is a particle-non-resolved type⁽³⁾. It is known that the latter type simulation provides a good representation of fluidized behavior with bubbles^(4,5).

In general, the number of particles in the applications of engineering interest is enormous, and numerical simulations using DEM are very computationally demanding. For this reason, it is necessary to reduce the computational load for many problems. There are two kinds of approach to reduce it. One is the reduction of the spring constant (stiffness) in the contact force model to increase the time step for calculation^(6,7), the other is the use of coarse grain model to reduce the number of particles. Fig. 4 shows the behavior of particles in a particle mixer simulated using a coarse grain model⁽⁸⁾. Here, liquid is added and capillary forces are acting between the particles due to liquid bridges. The original particle behavior is well represented by the proposed scaling rule for the forces acting on coarse particles. Similar scaling laws can be applied to various types of forces such as particle surface adhesion and lubrication forces.

Fig. 5 shows simulation results of the behavior of a large object in a fluidized bed ⁽⁹⁾. Such a setup is of interest, for example, in analyzing the behavior of refuse in a fluidized bed waste incinerator. In this calculation, the fluid flow calculation does not resolve the particle size scale of the fluidizing medium, but resolve the large-scale object⁽¹⁰⁾. The effect of object shape is also an important issue for applications such as fluidized bed waste incinerators, and the effect of non-spherical shapes is modeled by the Super-Ellipsoid model.

Key words

Granular flow, Gas-solid two-phase flow, Numerical simulation, Discrete particle simulation, Discrete Element Method

Figures

Fig.1 Flowing sand in hourglass

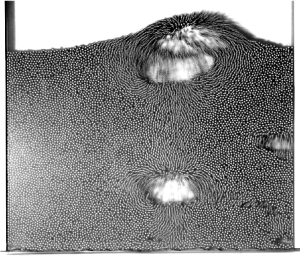
Fig.2 Bubbles formed in fluidized bed

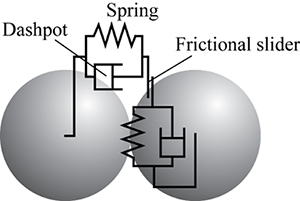
Fig.3 Contact force model of discrete element method

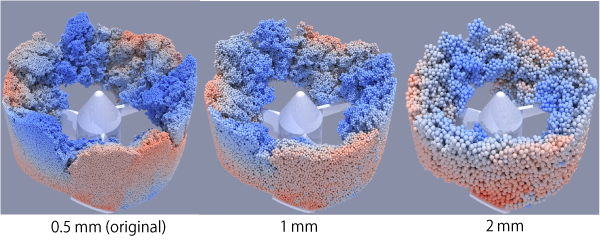
Fig.4 Motion of particles with capillary force in mixer⁽⁸⁾

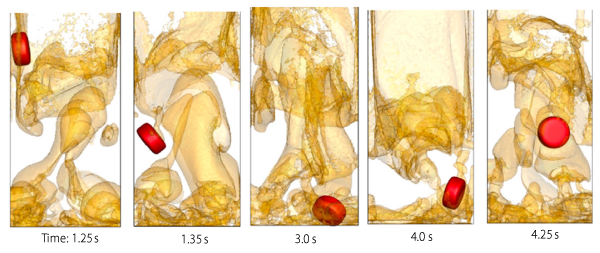
Fig.5 Motion of non-spherical large object in fluidized bed⁽⁹⁾

References

(1)	Tanaka, T., Flow of Granules, Journal of the Japan Society of Mechanical Engineers, Vol. 116, No. 1136 (2013), pp. 466-469.
(2)	Cundall, P.A. and Strack O.D.L., Discrete Numerical Model for Granular Assemblies, Geotechnique, Vol. 29 (1979), pp. 47-65.
(3)	Anderson, T. B., and Jackson R. A., Fluid Mechanical Description of Fluidized Bed, I&EC Fundamentals, Vol. 6 (1967), pp. 527-539.
(4)	Kawaguchi, T. and Tanaka, T., Tsuji, Y., Numerical Simulation of Fluidized Bed using the Discrete Element Method (the Case of Spouting Bed), Transactions of the Japan Society of Mechanical Engineers, Part B, Vol. 58, No. 551 (1992), pp. 2119-2125.
(5)	Tsuji, Y., Kawaguchi, T. and Tanaka, T., Discrete Particle Simulation of Two-Dimensional Fluidized Bed, Powder Technology, Vol. 77 (1993) , pp. 79-87.
(6)	Kobayashi, T., Tanaka, T., Shimada, N., Kawaguchi, T., DEM-CFD Analysis of Fluidization Behavior of Geldart Group A Particles Using a Dynamic Adhesion Force Model, Powder Technology, Vol. 248 (2013), pp. 143-152.
(7)	Washino, K., Chan, E.L., Tanaka, T., DEM with attraction forces using reduced particle stiffness, Powder Technology, Vol.325 (2018), pp. 202-208.
(8)	Hu, Y., Chan, E.L., Tsuji, T., Tanaka, T., Washino, K., Geometry similarity on interparticle force evaluation for scaled-up DEM particles, Powder Technology, Vol. 404 (2022), 117483.
(9)	Tsuji, T., et al., FPM-SE: a numerical model for dense gas-solid flows with large non-spherical object, Chemical Engineering Science, Vol. 264 (2022), 118149.
(10)	Tsuji, T., Higashida, K., Okuyama, Y., Tanaka, T., Fictitious Particle Method: A Numerical Model for Flows Including Dense Solids with Large Size Difference, AIChE Journal, Vol.60 (2014), pp. 1606-1620.