流れ 2003年12月号 目次
― 特集:動力飛行百周年 ―
| リンク一覧にもどる | |
ロケットポンプ内部に発生する極低温流体中のキャビテーション現象 (共著)
|
|
1. まえがき
我が国におけるロケット開発は液体ロケットが主流となっている. これらのロケットエンジンでは燃料である液体水素と液体酸素を200気圧以上もの高圧にして燃焼室に送り込んでいる. この役目を担っているのがターボポンプであり, いわばロケットエンジンの「心臓」とも言える要素である. しかしこのターボポンプ内部ではその高速回転のためインデューサと呼ばれる部品の周辺にキャビテーションが発生し, 1999年のH-IIの事故に見られるようにエンジンシステムに様々な悪影響を及ぼす. よってこのターボポンプ内部のキャビテーション現象を正確に予測することがロケットエンジンを開発する上で非常に重要になるが, 液体水素, 液体酸素などの極低温流体は水などの通常の液体と比較して液体の圧縮性が大きい, 気液の密度比が小さい, 温度降下量に対する蒸気圧の降下量が大きい, 不純物の混入が少ないなどの性質を持ち, そのためそのキャビテーション現象も水中のキャビテーションでは観察されないような現象を伴う. 本稿ではこのような極低温流体に特有のキャビテーション現象の基礎的な解析や, 現在のロケットエンジン開発について紹介し, 極低温流体中のキャビテーション現象の問題点について述べる.
2. キャビテーションに関する熱力学的効果の数値解析
極低温流体中のキャビテーションに特有の現象としてキャビテーションの熱力学的効果がある. これはキャビテーションの発生により周囲流体が蒸発潜熱を奪われるため温度が低下し, それにより周囲流体の飽和蒸気圧が低下, 新たな蒸気の発生が抑制されるという効果である. 極低温流体でこの熱力学的効果が顕著に現れる理由は以下の2点による.
(1) 流体では気液の密度比が小さいため, 同程度のキャビティ(気泡)を作るのにより多くの液体の蒸発を必要とし, そのため気液界面からより多くの蒸発潜熱を奪う.
(2) 極低温流体は水に比べて温度降下量に対する飽和蒸気圧の降下量が著しく大きい.
したがって液体酸素や液体水素ではこのキャビテーションの発生に伴う熱力学的効果により吸い込み性能の低下が大幅に抑制され, これがターボポンプの性能の維持に大いに役立っている. このキャビテーションに対する熱力学的効果を数値計算で予測することが可能となれば実機による試験回数や製作コストの大幅な削減につながると考えられる. しかしながら従来の研究では熱力学的効果の詳細なメカニズムは必ずしも明確にされておらず, そのモデルもインデューサの実験値や実験式を必要とするものが多く, 研究を要するところとなっている.
ここではより実現象に近いキャビテーションモデルを構築し, 数値解析により熱力学的効果を予測する手法を考案した. 本モデルではキャビティの形状は気液界面での圧力のバランスによって決定し, キャビティ界面の温度分布は蒸発に伴うエネルギバランスによって決定した.これを用いて2次元翼まわりに発生したシートキャビテーションの計算を行った. 計算は290Kの水と80Kの液体酸素, 90Kの液体酸素について行い, また比較のために熱力学的効果を考慮しない場合の計算も行った. その結果を図1, 2に示す. これらの計算においてキャビテーション係数は同一である.
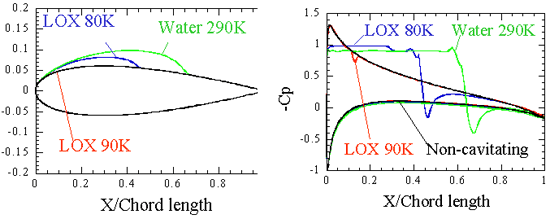
図1: キャビティ形状 図2: 圧力係数分布
上図からもわかるように, 同一のキャビテーション係数であるにも関わらず, 常温水ではキャビティの大きさが大きいのに対し液体酸素では熱力学的効果が大きく, キャビティの縮小が顕著にみられることがわかる. なお, 本計算では流れのレイノルズ数の増加とともにキャビテーションに対する熱力学的効果が減少していく傾向が見られた. H-IIAロケットLE-7エンジン液体水素ポンプインデューサについては小さな流量比の範囲で熱力学的効果が著しく減少し, これが引き金となってインデューサに旋回失速現象が発生した. このようなことが今後解決すべき問題となっている.
- 3. 気泡核生成の分子動力学的解析
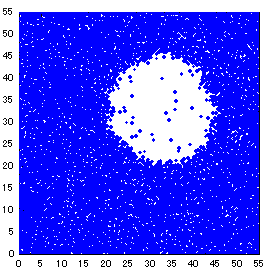
水中には多量の気体(窒素, 酸素)がとけ込んでおり, キャビテーションが発生する際にはこれらが気泡核となることが知られている. 極低温流体では液体中にこのような不純物の存在が少なく, そのため飽和蒸気圧以下の圧力になっても気泡が生成しない可能性がある. このような状態での気泡の生成は分子スケールのオーダーで起こる現象と考えられるため, この現象を解析するには液体を分子の集合体として捉えなければならない. ここでは分子動力学法を用いて液体酸素中に発生する気泡の生成, 成長プロセスを観察し, 考察を行った. ここでは50万個の分子を用いて液体酸素を表現し, 分子は単原子Lennard-Jones分子を仮定している. 図3に液体酸素中の気泡と密度及び圧力の時間履歴を示す. 単位はLennard-Jonesポテンシャルのバラメータσ, εと分子質量mで無次元化してある. この図から液体には発泡する前でも負圧(張力)がかかっており明らかに飽和蒸気圧より低い状態にあること, 密度をある状態以下に下げると液体中で発泡が起こり圧力が急激に増加していることなどがわかる.
図3: 液体酸素中の気泡
図4: 圧力及び密度の時間履歴
4. ロケットポンプインデューサの非定常試験
ターボポンプは推進剤タンク重量を軽減するために高速回転することでポンプ入口の吸込圧力を限界まで低減して運転される. そのためロケットポンプインデューサは激しいキャビテーション状況下にさらされることになる. このような状況下では, 旋回キャビテーション(Rotating Cavitation)に代表されるように, インデューサに発生するキャビテーションによる振動が問題になってくる.
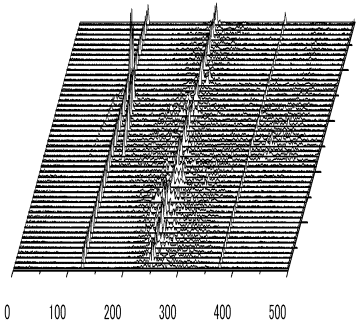
図5: インデューサ軸振動FFT解析結果
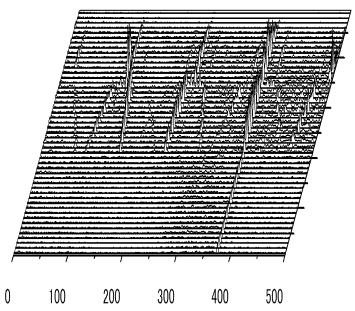
従って, より高い吸込能力と安定作動に関するインデューサの設計指針を得る為にインデューサ内部流れの観察を行うことが重要であるといえる. ここでは実験によってキャビテーションによってインデューサにひきおこされる非定常現象について解析した. 図5にインデューサ軸振動FFT解析結果を, 図6にインデューサ変動圧FFT解析結果を示す. 軸振動のウォーターフォール図にはインデューサの回転周波数(7500rpmでω=125Hz)の2倍, 3倍の成分(2ω=250Hz, 3ω=375Hz)のピークが現れている. そして減圧していくと, まず初めに1~1.2ωの周波数にピークが現れている. つまりこれはインデューサの回転よりも速い回転数で回転するキャビテーションで, 回転非同期キャビテーション(Rotating Cavitation: R.C.)と呼ばれる現象である. そしてこのR.C.は徐々に回転周波数(1ω)に近づき, 1ωになると同時に1ωの回転成分よりも遙かに大きなピークが現れている. つまりこれはインデューサと同じ回転数で回転するキャビテーションで回転同期旋回キャビテーションと呼ばれる現象である. また変動圧のウォーターフォール図には変動圧センサのポートとインデューサの3枚羽根との干渉による3ωの成分のピークが現れていることがわかる. そして軸振動と同じくR.C.に続いて回転同期R.C.が発生し, そのピークが現れている. また旋回キャビテーションによるピークが消えた後に20Hz付近にピークが現れている. これはキャビテーションサージ(Cavitation Surge: C.S.)と呼ばれる現象である. R.C.がインデューサまわりを回転する2次元の非定常現象であるのに対して, C.S.はインデューサの軸方向に振動する1次元の非定常現象である.
5. 高圧液体水素供給系の動的挙動の解析
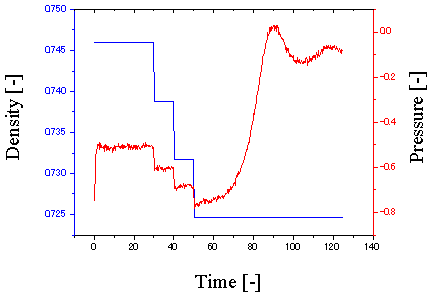
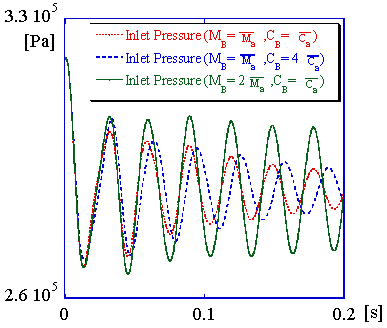
インデューサに発生するキャビテーションによって, ポンプのみならずエンジンシステム全体としても様々な振動問題が生じる. 近年注目されている現象としては旋回キャビテーションとキャビテーションサージがある. これらの不安定現象については発生条件や抑止例などが報告されているが, 発生メカニズムや定量的設計指針などは明確に解明されていない. ここではLE-7エンジンの液体水素供給系のタンクからポンプ出口配管までを対象とし, 1次元非線形圧縮性流れ解析によってタンクの圧力降下とポンプ下流側の圧力降下に対するシステムの応答をそれぞれ数値シミュレーションし, ポンプのキャビテーションによる動特性がシステムの安定性に与える影響について解析を行った. 右図にその一例として,ポンプの動特性パラメーターであるキャビテーションコンプライアンス(Cb)やマスフローゲインファクター(Mb)のシステムの安定性に与える影響を示す. 図はタンク圧力が急激に10% 降下する時のポンプ入口圧力の変化を示している. この図よりCbが大きいほど振動周波数が低くなり, またMbが大きいほど振動振幅が大きくなり, かつ動的不安定性が増加することがわかる.
図7: キャビテーションコンプライアンス(Cb)及びマスフローゲインファクター(Mb)の影響
6. おわりに
キャビテーションにまつわる不具合を克服することは現在でもロケット開発において非常に重要な課題であり, 日夜研究が進められている.
今後もさらなる研究が望まれるところである.
参考文献
[1] 上條謙二郎, 平田邦夫, “ロケットを飛ばす”, オーム社
[2] 上條謙二郎, “我が国のロケットエンジン開発での経験”, 日本機械学会誌 4月号 (2003), Vol. 116. pp.64-67
[3] T. Tokumasu, Y. Sekino and K. Kamijo, “ A New Modeling of Sheet Cavitation Considering the Thermodynamic Effects”, CAV2003 (2003) GS-16-003
[4] T. Tokumasu, K. Kamijo, M. Oike and Y. Matsumoto, “Molecular Dynamics Study of the Nucleation of Bubble”, CAV2001 (2001) A1-005
[5] 瀧田純也, 東北大学修士論文(2002)
[6] 全相仁, 徳増崇, 上條謙二郎, “高圧液体水素供給系の動的挙動の解析”, ターボ機械, Vol.31 (2003), pp.11-18