流れ 2007年8月号 目次
― 流体と騒音:汎用ソフトウェア特集 ―
| リンク一覧にもどる | |
流体騒音解析ソフトウェアCAA++
~非線形音響ソルバによる流体騒音の数値予測~
|
|
1. はじめに
最近,流体騒音の数値解析をテーマにした研究が盛んになり,製品開発や設計の現場でも活用されるようになってきた. 流体騒音の予測手法には幾つかの方法があるが,いずれの場合も,流体と音のスケールの違いから,空力騒音を定量的に予測するためには,通常,膨大な計算量が必要である. 本稿で紹介する CAA++ の非線形音響ソルバ (NLAS)(1) は,計算量を従来の方法に比べ大幅に低減し,且つ,精度を高めることが期待される解析手法であり,米国 Metacomp Technologies 社が開発したソフトウェアである.
CAA++ には, NLAS の他に,音響学的類推による解析的手法や Hybrid LES/RANS ( LNS )等の流体計算による直接解法も利用できる. しかし,音響学的類推による方法は,流体と音の相互作用,壁面での音の反射や障害物による閉塞,回析の効果を考慮することができない. また, Hybrid LES/RANS ( LNS )による直接計算は,膨大な計算量を必要とするため計算領域が大幅に制限される.
NLAS は,流体と音の相互作用,壁面での反射,障害物による閉塞や回析の影響を考慮することができ,擾乱(平均値からのずれ)に注目した支配方程式を解くため,流れと音のスケールの違いの問題も大幅に低減可能な解析手法である.
表1に CAA++ で利用できる解析方法と特徴を示す. NLAS は,定常解が存在する場合に限定されるが,今後,期待される流体騒音解析手法である. 次節に NLAS の詳細を示す.
表 1 . CAA++ で利用できる解析方法と特徴
|
NLAS ( Non Linear Acoustic Solver ) |
Waveprop1 ( 体積音源用) Wavepropf ( 表面音源用) |
LNS ( Limited Numerical Scale ) |
| 解析手法 | 定常解: RANS or LNS 非定常音響計算: 粘性擾乱方程式 |
音源計算: LNS 音の伝播:音響学的類推( FW-F ) |
Hybrid RANS/LES |
| 解析可能な音源 | 単極 , 2重極 , 4重極子 | 2重極子 | 単極 , 2重極 , 4重極子 |
| 壁面反射・閉塞 | ○ | × | ○ |
| 流体 - 音の相互作用 | ○ | × | ○ |
| 計算コスト | ○ | ○ | △ |
| その他の特長 | 音響解析用の領域・メッシュによる計算量低減 | 移動音源可 | LEST によるカットオフ変動値のモデル化 |
2.非線形音響ソルバ( NLAS )
NLAS の支配方程式(粘性擾乱方程式)を以下に示す.
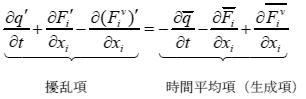
粘性擾乱方程式は,ナビエストークスの式を擾乱項(左辺)と時間平均項(右辺)に変形したものである . したがって, NLAS の計算により左辺の変動値(ダッシュのついた変数)が求まる.
ここで,右辺は予め RANS による定常計算(あるいは非定常計算の時間平均)を行って求め,その結果を NLAS の計算では生成項(右辺)として与える. 次式は右辺項の詳細である . 変動値の時間平均項が含まれているが,これらの値は, Kraichnan(2) の方法に非等方性や移流の効果を加えたものであり, 定常解の乱流エネルギ k から統計的な手法を用いて求める(1).
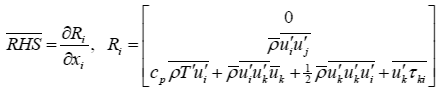
次に, NLAS を用いた解析作業の流れ ( ①~④ ) を図2に示す.
① RANS による定常計算(あるいは, LES, LNS 等による非定常計算)
② NLAS の式の右辺の値を求める. CAA++ の中では,これらの値は自動的に音響用データファイルに保存されている.
③音響解析用の計算領域とメッシュの生成(オプション)
図2下のイメージ図に示すように,音響解析の計算領域は流体計算と必ずしも同じである必要はなく, CAA++ のツールを用いて音響解析に必要な領域まで小さくすることができる.また,図3に示すとおり,壁面境界層メッシュは NLAS では不要である. したがって,計算領域を小さくし,メッシュ数を減らすことで,計算量を大幅に低減することが可能である.
④ NLAS による音響計算
⑤結果の分析( FFT )
CAA++ の FFT 分析機能には,オクターブ分析 (1/1, 1/3), 窓関数( Bartlett, Welch, Hann ),移動平均処理等が装備されている.

図 2 LAS による音響解析作業の流れ
 |
 |
(a) 流体計算用メッシュ |
( b )音響解析用メッシュ |
図 3 流体計算用メッシュと音響解析用メッシュの違い |
|
3. 解析事例
平板に置いたドアミラー形状周りの流れを対象として, NLAS による空力騒音解析を行い,測定データと比較する(3).
ドアミラーの形状は, 0.2m の半円筒に r=0.1m の 1/4 球状を取付けた形をしており,流入速度は 200km/hr とする. 図 4 に示す位置にプローブを2箇所( Probe111 及び Probe123) 設け,各プローブでの音圧レベルを予測する.
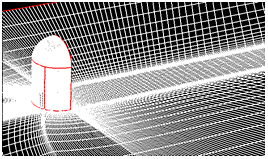
図5(左図)に物体近傍のメッシュを示す. 物体壁面近傍は Y+<1 になるように境界層を張り,総メッシュ数は約 50 万とした.
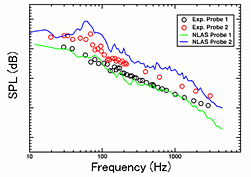
最初に Cubic k-ε乱流モデルを用いて RANS による定常計算を行った後,図5(右図)に示すとおり壁近傍のメッシュを粗くし,また,外側境界を遠方場吸収境界条件として,流体解析の領域より小さく取った音響解析用のメッシュを作成した . 音響解析用のメッシュ数は約 34 万である . RANS 計算結果の解は,音響解析用メッシュに内挿した後,NLAS による非定常計算を実施する . 図6,図7,図8は,それぞれ NLAS,Waveprop1( 音響学的類推 ) , LNS(Hybrid LES/RANS) により求めた周波数に対する音圧レベルの予測値を実測値と共にプロットした結果をそれぞれ示す.
図6に示すとおり, NLAS の結果は, Probe 111 でやや過小しているものの概ね実測値と一致している.
一方,図7に示すとおり, Waveprop1 の解析結果は,高周波数領域では実測値に近い値であったが,低周波数領域の音圧レベルは一致していない .また, NLAS で捉えているミラー近傍後流の間欠的な剥離泡の発生は Waveprop1 では捉えていない.
LNS の結果については,図 8 に示すとおり,高周波数領域の値が実測値と一致していない . 低周波数領域については, Probe111 では概ね一致しているが, Probe 123 では過大評価しており, NLAS の結果と比べても誤差が大きいことが分かる.
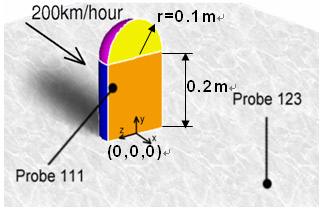
図 4 計算モデルとプローブの位置
 |
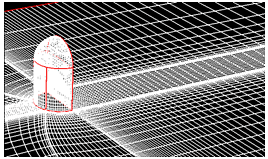 |
図5 メッシュ(左:流体計算用 : 約 50 万 , 右:音響計算用 : 約 34 万) |
|
 |
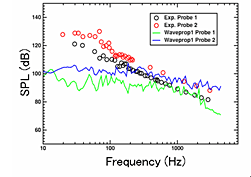 |
図6 周波数 - 音圧レベル( NLAS ) |
図7 周波数 - 音圧レベル( Waveprop1 ) |
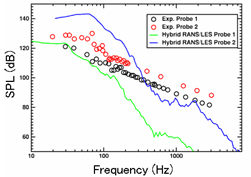 |
| 図8 周波数 - 音圧レベル( LNS ) |
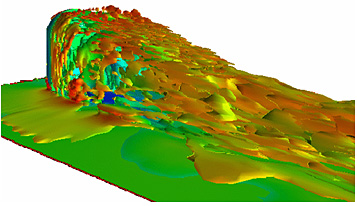 |
| 図9 渦度分布の瞬間値( NLAS ) |
4. まとめ
本稿では,流体騒音解析ソフト CAA++ の内,非線形音響ソルバ (NLAS) に焦点を当て概要と事例を紹介した. NLAS は,流体と音波の相互作用の考慮が可能で,且つ,計算時間や精度の上でも優れた流体騒音解析手法として今後期待される 解析手法である.
参考文献
| (1) | Batten P.,Ribaldone, E., Chakravarthy, S.;Towards a Generalized Non-Linear Acoustics Solver;AIAA 2004-3001, 2004. |
| (2) | Kraichnan, R.H., Diffusion by a Random Velicity Field, Physics of Fluids, 13(1), 1969. |
| (3) | Hold, R., Brennis, A., Eberle, A., Schwartz, V., Siegert, R., Numerical Simulation of Aeroacoustic Sound Generated by Generic Bodies Placed on a Plate: Part I- Prediction of Aeroacoustic Sources, AIAA 99-1896, 1999. |


