流れ　2018年1月号　目次

―　特集テーマ：2017年度年次大会　― 巻頭言 （本澤，黒澤） 機能性流体工学の研究展開 西山秀哉（東北大学） イルカの体表面から着想を得た抵抗低減法と熱伝達促進 萩原良道（京都工芸繊維大学） レーザー誘起マイクロジェットの軟質材料への注入深さに関する研究 遠藤奈々美，河本仙之介，田川義之（東京農工大学） 液体急加速時における新しいキャビテーション数の提案 木山景仁（東京農工大学），Zhao Pan（ユタ州立大学），田川義之（東京農工大学），Jesse Daily（Naval Undersea Warfare Center），Scott Thomson（ブリガムヤング大学），Randy Hurd，Tadd Truscott（ユタ州立大学） 粘弾性流体を利用したニュートン流体の乱流維持機構の解明 堀本康文，後藤晋（大阪大学） 　｜　リンク一覧にもどる　｜

 

粘弾性流体を利用したニュートン流体の乱流維持機構の解明

堀本 康文， 後藤 晋 大阪大学

１．緒言

　 日本機械学会2017年度年次大会において，光栄にも優秀講演表彰をいただきました．この場を借りて，選考委員会および日本機械学会流体工学部門の皆様に御礼申し上げます．また，ニュースレター執筆の機会を賜りましたことも，関係者の皆様に御礼申し上げます．本稿では，表彰をいただいた表題の研究内容を紹介いたします．

　 乱流とは，大小様々な渦の相互作用による複雑な流体運動です．水の乱流に高分子や界面活性剤をほんのわずか添加するだけで，乱れが劇的に抑制されることが半世紀以上も前から知られています^[1]．この乱流抑制現象は流れの壁面摩擦抵抗を著しく低減するので，簡便な乱流制御の手法として広く研究されてきました^[2,3]．また，高分子や界面活性剤の水溶液は粘弾性を有する非ニュートン流体で，そのレオロジー特性の計測も盛んに行われています．

　 本研究では，この現象を別の視点から捉えます．つまり，水の乱流中にもともと存在する，乱流を維持するための物理機構が添加剤水溶液の粘弾性により阻害されて，上述の乱流抑制現象が発現したと考えます．すると，添加の前後での乱流の相違点は，粘弾性に対する乱流維持機構の応答だと解釈でき，それを系統的に調べることで水，つまりニュートン流体の乱流の維持機構を理解できるという発想に至ります．

 

２．流れ場と実験手法

　 希薄な添加剤水溶液を実験的に扱うためには，よく制御された乱流を実現できる実験系が不可欠で，そのためには閉じた系を用いた実験装置が便利です．容器内に充填した流体の乱流を容易に維持できる系の一例として，歳差運動をする容器内流れがあります．ここで，歳差運動とは回転する物体の回転軸（自転軸）そのものが他の軸（歳差軸）まわりに回転する運動のことです（動画1）．

動画1: A precessing sphere. In this study, the axes of the spin (Ω_s) and precession (Ω_p) are perpendicular to each other.

 

　 本研究では，容器形状として最も対称性の高い球体を用いました．容器形状および自転軸と歳差軸のなす角を固定すると，容器内のニュートン流体の運動は二つの無次元パラメタ、レイノルズ数Re=a²Ω_s/ν とポアンカレ数Po=Ω_p/Ω_s のみで決まります．ここで，aは球半径，νは流体の動粘度，Ω_s およびΩ_pはそれぞれ自転と歳差の角速度の大きさを表します．

　 実験装置の概略を図1に示します．内部を球状（半径90mm）にくりぬいた円柱形容器を回転する実験台の上で自転させることで，容器の歳差運動を実現しました．実験台と容器の回転はそれぞれ別のステッピングモータにより制御しました．作動流体にあらかじめ可視化用の粒子を懸濁し，球中心を通り自転軸に垂直な断面上にレーザーシート光を入射することで，内部の流れの可視化観察および粒子画像流速測定（PIV）を実施しました．また，実験装置のまわりの空気温度を高精度に制御することで，作動流体の温度が20±0.1℃の範囲内で実験を行いました．

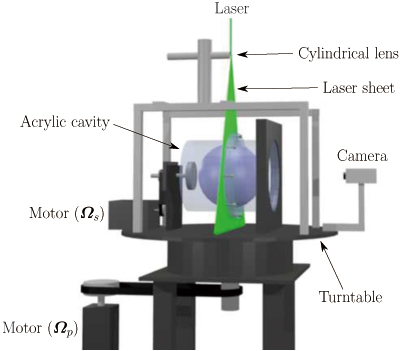
図1: Experimental apparatus. Visualized flows are recorded by a camera fixed on the turntable.

　 本研究では，陽イオン性界面活性剤セチルトリメチルアンモニウムクロリド（CTAC．分子量320.00）を水に添加しました．CTAC水溶液に適当な対イオンを添加すると，界面活性剤ミセルは細長いひも状の構造に成長して水溶液は顕著な粘弾性を示します．本研究では，対イオンにサリチル酸ナトリウム（NaSal．分子量160.10）を用いました．CTACとNaSalの濃度はどちらも質量濃度50ppmとしました．なお，CTAC水溶液は非常に希薄なので，その動粘度は同温度の水と等しいとしてレイノルズ数を評価しています．

 

３．結果

　 動画2に，可視化した水とCTAC水溶液の乱流を示します．パラメタはRe=4.0×10⁴，Po=0.1です．先行研究により，水の乱流はReが十分大きい場合（Re≧5000）に，Po≈0.1で最も発達することが知られます^[4]．そこで，以下ではパラメタを上述の値に固定します．可視化から，水の乱流中の細かい構造がCTAC水溶液の乱流では存在せず，確かに乱流抑制現象が生じていることが確認できます．

動画2: Visualization of turbulence of (left) water and (right) the CTAC solution
(50 ppm). Re=4.0×10⁴，Po=0.1.

 

　 次に，この観察結果をPIVにより定量化します．図2にPIVの結果から算出した渦度の2乗（エンストロフィ）の時間平均の分布を示します．ここで，小さな渦ほど乱流中の渦度分布への寄与が大きいので，この量は乱流中の小スケール渦に対応することに注意します．図2より可視化で観察した小スケール渦の抑制を定量的に確認できます．

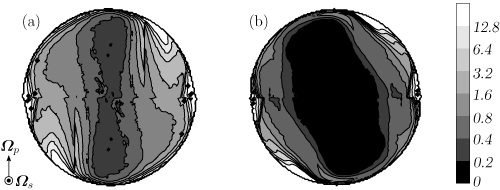
図2: Temporally averaged enstrophy field of turbulence of (a) water and (b) the CTAC solution (50 ppm). Re=4.0×10⁴，Po=0.1.

　 続いて，乱流中の大スケール渦に対するCTAC添加の影響を調べます．そのために，PIVで得た速度場から時間平均流速場を算出しました．図3に，動画2の乱流の時間平均流速場を示します．水の乱流[図3(a)]には，右上と左下に大規模な渦構造が存在します．ニュートン流体の乱流の数値シミュレーション^[5]によれば，この渦構造は乱流中に存在する1対の大きな渦管構造に対応します．一方，CTAC水溶液では大スケール渦も粘弾性の影響を受けて，その大規模渦構造周辺の流速が著しく低減されます．しかし興味深いことに，CTAC水溶液の乱流中にも，右上と左下に水と同様の大規模渦構造が存在します[図3(b)]．

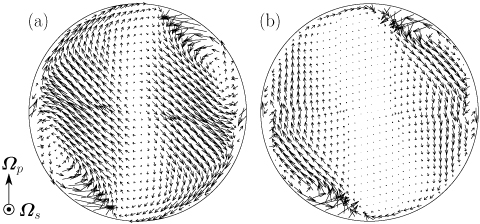
図3: Temporally averaged velocity field of turbulence of (a) water and (b) the CTAC solution. Re=4.0×10⁴，Po=0.1.

 

４．考察

　 前節で示したCTAC添加が乱流中の小スケールと大スケールの渦にそれぞれおよぼす影響から，水の乱流を維持する物理機構を考えます．緒言で述べたように，添加剤による乱流抑制現象は広く研究され，その発現条件も理論的によく議論されています．乱流抑制現象の発現に関する理論^[6,7]によると，乱流中に存在する渦の時間スケールと水溶液の粘弾性の時間スケールが同程度になると乱流が抑制されます．このとき，この時間スケールのマッチングが生じる大きさの渦のもつ運動エネルギーが粘弾性により低減します．

　 ここで，球体内の乱流の維持機構には二つの可能性があることに注意します．一つ目は，壁面近傍の高せん断速度領域で生成された小スケール渦が，大規模渦構造[図3(a)]の誘起する流れにより球内部に移流されて乱流が維持されるという機構です．しかし，実験結果からこの維持機構は否定されます．なぜなら，CTAC添加により小スケール渦が強く抑制される乱流[動画2, 図2(b)]でも，水の乱流と同様に大規模渦構造が存在するからです[図3(b)]．

　 二つ目は，乱流中の渦が自身のまわりに形成するひずみ速度場を介して，より小スケールの渦へと運動エネルギーを受け渡すことを繰り返し，乱流中の大小様々な渦を形成するという物理機構です．この機構はエネルギーカスケードとよばれ，壁から離れた乱流中の渦の生成機構として知られます．大規模渦構造から始まるエネルギーカスケードにより乱流が維持されるとすると，以下のように実験結果を説明できます．つまり，大規模渦構造は自身のまわりにより短い時間スケールで旋回する小さな渦を形成し，形成された渦はさらに小さな渦を形成します．その結果，乱流中には渦の大小に応じて長い時間スケールから短い時間スケールまでの渦が存在することになります．この渦の階層構造の途中で渦と水溶液の粘弾性の時間スケールのマッチングが生じると，階層間の運動エネルギーの伝達がそこで止まり，マッチングした渦の大きさ以下の渦は形成されなくなります．その結果，「大規模渦構造は存在するにもかかわらず，小スケール渦は抑制される」という結果が得られます．

 

５．結言

　 水，つまりニュートン流体の乱流の維持機構を理解するために，界面活性剤CTACを添加した場合に生じる乱流抑制現象を利用する手法を考案しました．その有用性を示すため，歳差運動をする球体内の水とCTAC水溶液の乱流に可視化観察とPIVを実施し，乱流中の小スケールと大スケールの渦に対するCTAC添加の影響を実験的に調べました．そして，CTAC添加により乱流中の小スケール渦が著しく抑制される場合であっても，大スケール渦は添加の影響を受けつつも水の場合と同様に存在するという結果を得ました．この実験結果を説明する乱流維持機構を考察し，この球体内の乱流は大規模渦構造から始まるエネルギーカスケードにより維持されることを示しました．

　 本稿は我々の最近の研究結果^[8]の紹介ですが，我々はCTAC水溶液の他のパラメタでの実験だけでなく，粘弾性の時間スケールが異なる高分子の水溶液でも実験も行い，上記の考察を裏付ける結果を得ています．

　 本研究では，流れ場として歳差運動をする球体内流れを採用しました．この系に限らず，近年は数値シミュレーションの助けもあり，壁面近傍の乱流の維持機構の理解が急速に進んでいます．本稿で考案した手法は，それら数値シミュレーションによる研究と連携しながら，他の系における乱流の維持機構解明に実験的にアプローチする手法として有効であると期待しています．

 

謝辞

　 本研究の一部は，JSPS科研費（24360071，16H04268）の助成を受けました．

 

References

[1]	Toms, B. A., Some observation on the flow of linear polymer solutions through straight tubes at large Reynolds numbers, Proc. 1st Intl. Congr. on Rheology, Vol. 2 (1948), pp. 135-141.
[2]	Zakin, J. L., Lu, B. and Bewersdorff, H.-W., Surfactant drag reduction, Rev. Chem. Eng., Vol. 14 (1998), pp. 253-320.
[3]	White, C. M. and Mungal, M. G., Mechanics and prediction of turbulent drag reduction with polymer additives, Annu. Rev. Fluid Mech., Vol. 40 (2008), pp. 235-256.
[4]	Goto, S., Matsunaga, A., Fujiwara, M., Nishioka, M., Kida, S., Yamato, M., and Tsuda, S., Turbulence driven by precession in spherical and slightly elongated spheroidal cavities, Phys. Fluids, Vol. 26 (2014), 055107.
[5]	Goto, S., Shimizu, M. and Kawahara, G., Turbulent mixing in a precessing sphere, Phys. Fluids, Vol. 26 (2014), 115106.
[6]	Lumley, J. L., Drag reduction in turbulent flow by polymer additives, J. Polymer Sci.: Macromol. Rev., Vol. 7 (1973), pp. 263-290.
[7]	Tabor, M. and de Gennes, P. G., A cascade theory of drag reduction, Europhys. Lett., Vol. 2 (1986), pp. 519-522.
[8]	Horimoto, Y. and Goto, S., Sustaining mechanism of small-scale turbulent eddies in a precessing sphere, Phys. Rev. Fluids, Vol. 2 (2017), 114603.