流れ 2005年9月号 目次
― レオロジー ~非ニュートン流体の流動~ ―
| リンク一覧にもどる | |
Back to the Future ―非ニュートン流体からニュートン流体へ―
 新潟大学 長谷川富市 |
流体は力学的挙動を基にニュートン流体と非ニュートン流体に分けられる.力学的挙動は対象となる物質の構成方程式によって表わされ,ニュートン流体については次式の,いわゆるニュートンの粘性法則が成り立つ.
| (1) |
ここに,![]() ,
,![]() はそれぞれ応力テンソル,ひずみ速度テンソルの反変成分,
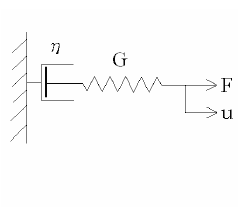
はそれぞれ応力テンソル,ひずみ速度テンソルの反変成分,![]() は粘性係数(粘度)である.式(1)が運動方程式と結びつくとNavier-Stokes方程式となり,水,空気,油などはこれにより良く記述される.一方,非ニュートン流体は,ニュートン流体に属さない流体が非ニュートン流体であるという補集合的定義によれば,式(1)によらない流体を全て包含することになり多種多様な物質を含むことになる.このなかでよく知られている流体は,粘弾性流体,べき乗則流体,ビンガム流体であるが,ここでは紙面の関係で粘弾性流体についてのみ述べる.粘弾性流体は,その名前の示すように粘性と弾性を併せ持った流体であり,モデル的に表わせばバネ(弾性)とダッシュポット(粘性)の直列結合として表わされる(図1).図中において
は粘性係数(粘度)である.式(1)が運動方程式と結びつくとNavier-Stokes方程式となり,水,空気,油などはこれにより良く記述される.一方,非ニュートン流体は,ニュートン流体に属さない流体が非ニュートン流体であるという補集合的定義によれば,式(1)によらない流体を全て包含することになり多種多様な物質を含むことになる.このなかでよく知られている流体は,粘弾性流体,べき乗則流体,ビンガム流体であるが,ここでは紙面の関係で粘弾性流体についてのみ述べる.粘弾性流体は,その名前の示すように粘性と弾性を併せ持った流体であり,モデル的に表わせばバネ(弾性)とダッシュポット(粘性)の直列結合として表わされる(図1).図中において
 |
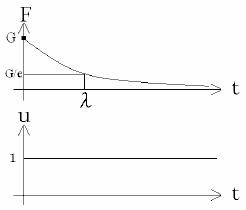 |
図1 マクスウェルモデル |
図2 変位uに単位ステップ関数を加えた場合の力Fの推移 |
ηはダッシュポットの粘性係数,Gはバネの弾性係数,Fは力,uは変位である.これからFとuを関係付ける構成方程式が次式のように得られる.
| (2) |
上式を1次元マクスウェルモデルという.式中のλは時間の次元を持ち![]() であって緩和時間と呼ばれる.ここで緩和時間について若干の説明を加えよう.図1のマクスウェルモデルに変位uの単位ステップ関数1(t)を加え,このとき生じるFを式(2)により求めると次に示す式(3)となり,時間を横軸にとって表わすと図2のようになる.すなわち,
であって緩和時間と呼ばれる.ここで緩和時間について若干の説明を加えよう.図1のマクスウェルモデルに変位uの単位ステップ関数1(t)を加え,このとき生じるFを式(2)により求めると次に示す式(3)となり,時間を横軸にとって表わすと図2のようになる.すなわち,
1(t)=0 (t<0) , 1(t>0) について
| (3) |
t=0におけるFはバネの伸びの初期値に対応した値Gを示すが,時間の経過につれてダッシュポットが伸びるためバネの伸びは減少しFも減衰する.t=λにおいてはF=Ge-1となりFはt=0における値の1/e に緩和する.λが大きい場合は応力が長時間緩和しないことになり弾性体としての性質が強く,逆にλが小さい場合は流体の性質が強いことになる.
さて,現実の流体の流動場を解析するためには式(2)を3次元構成方程式に拡張する必要がある.この拡張には対流座標の考えを使うがその過程は省略し,結果のみを記すと式(4)のようになる.
| (4) |
上式において![]() は
は![]() に関する実質微分と呼ばれ以下の式で表わされる.
に関する実質微分と呼ばれ以下の式で表わされる.
| (5) |
ここに,![]() は速度ベクトルの反変成分であり,
は速度ベクトルの反変成分であり,![]() を2個含む項については
を2個含む項については![]() を省略している.すなわち
を省略している.すなわち![]() などである.
などである.
さて,式(5)を以下の単純せん断流
| (6) |
について解くと( ![]() とおいて )
とおいて )
| (7) |
| (8) |
を得る.![]() を測定すれば式(7)によって
を測定すれば式(7)によって![]() が求まる.この測定のためには円錐平板型レオゴニオメータや流動複屈折法が用いられるが,弾性の小さい場合や高せん断速度域では無力となってしまいこのような場合に有効な測定法は確立されていない.現在,測定上の困難さはあるが唯一有効と思われるものはジェット推力や反力を利用する方法である.
が求まる.この測定のためには円錐平板型レオゴニオメータや流動複屈折法が用いられるが,弾性の小さい場合や高せん断速度域では無力となってしまいこのような場合に有効な測定法は確立されていない.現在,測定上の困難さはあるが唯一有効と思われるものはジェット推力や反力を利用する方法である.
筆者らは以前ジェット反力法を用いて希薄高分子溶液の弾性力(あるいは緩和時間)を測定した.この過程で溶媒である水についても微小ではあるが弾性力の存在が示された(1).図3にこの結果を示す.他にも水の弾性力を測定したという報告がある(2).著者等は最近再びこの問題を取上げ,細孔を通過する流れの反力を測定しNavier-Stokes方程式による数値計算結果と比較した(3).この結果を図4に示す.縦軸は無次元反力( ![]() ),横軸はレイノルズ数(
),横軸はレイノルズ数(![]() )である.これによれば,孔径の大きい場合は反力の実験値と数値計算結果はほぼ一致しているが,微小孔については実験値が数値計算値よりもはるかに小さくなっており,弾性力の存在を示唆している.
)である.これによれば,孔径の大きい場合は反力の実験値と数値計算結果はほぼ一致しているが,微小孔については実験値が数値計算値よりもはるかに小さくなっており,弾性力の存在を示唆している.
以上述べたように,粘弾性流体の研究はニュートン流体の知見に基づいて発展してきたが,現在は逆に粘弾性流体に関する研究結果が水の流動特性を見直すきっかけを与えている.流体力学におけるBack to the Futureではないだろうか.
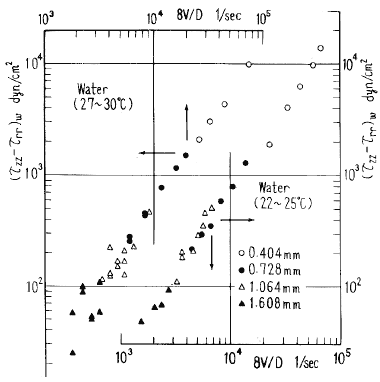
図3 細管内流れで生じた水の弾性力
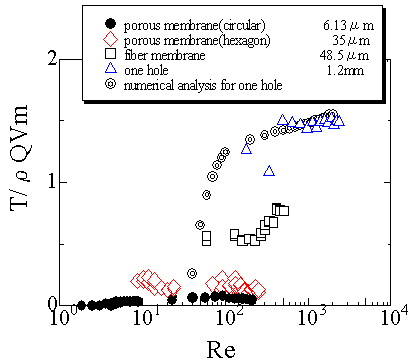
図4 細孔を通る水の流れの無次元反力
文献
- 長谷川富市,日本機械学会論文集(第2部)44巻381号1606-1615頁.または,Tomiichi Hasegawa, Bulletin of the JSME., 22-163, January, 1979, pp.54-62.
- Oliver, D. R. and McSporran, W. C., Deformation and Flow in High Polymer Systems, 1968, Macmillan(Proc. Brit. Soc. Rheology), 1966, pp.199-209.
- 日本流体力学会2004年会講演論文集,2004, 274-275頁.

