流れ　2005年9月号　目次

―　レオロジー ～非ニュートン流体の流動～　― Back to the Future ―非ニュートン流体からニュートン流体へ― 長谷川富市（新潟大学） 剛直な高分子シゾフィランの液晶の流動特性 武政 誠（日本学術振興会特別研究員）、西成 勝好（大阪市立大学） 嚥下食塊の流動解析とその応用 水沼 博（首都大学東京） オプティカル・レオメトリーとその応用 高橋勉（長岡技術科学大学） 非ニュートン流体の数値流動解析　－流体内部構造からのアプローチ－ 山本 剛宏（大阪大学） 編集後記 内田 憲（東芝），辻本 公一（三重大学），船橋 茂久（日立製作所），石本 淳（東北大学） 　｜　リンク一覧にもどる　｜

 

非ニュートン流体の数値流動解析　－流体内部構造からのアプローチ－

大阪大学 山本剛宏

　非ニュートン流体には，実に多くの種類の流体が含まれます．文字通り，非ニュートン流体の定義はニュートン流体，すなわち，応力が変形速度の1次式（ニュートンの粘性則）で記述できるような流体，ではないものを言うわけですから，多くの種類の流体が含まれるのも，当然のことかもしれません．

　例えば，高分子流体，種々のサスペンション（粒子懸濁液），コロイド，液晶，界面活性剤溶液，エマルションなどは，非ニュートン流体です．身の回りのもので例を挙げてみると，プラスッチック成形品の原材料や，生体由来の液体の多くは高分子溶液ですし，粘土やピッチはディスク状の鉱物粒子のサスペンションです．ペンキのような塗料も，母材に顔料の粒子が分散したものです．また，化粧クリームも分散系と見ることができます．ファイバー・サスペンション（繊維懸濁液）は，繊維強化プラスチック（FRP）の原料として知られています．高分子の液晶は，伸長流れで高配向度が実現されるという特性を活かして，液晶紡糸により防弾チョッキや工業用のワイヤーなどに使用される高強度繊維として利用されています．日常品である石鹸や洗剤は，界面活性剤の代表例ですし，マヨネーズやドレッシングのような食品はエマルションです．

　このように，非ニュートン流体は，種々の工業製品，日常品の原材料として利用されています．そして，製品の製造プロセス（各種の成形加工や輸送など）や，製品の使用（ペンキやクリームを塗る，食品を食べる，など）の際に「流れ」現象が現れ，流れ中の流体の挙動が製造効率や，非ニュートン流体のもつ種々の機能性の発現に影響します．したがって，非ニュートン流体の流動挙動に関する知見を得ることが大切になってきます．

　我々の研究室では種々の非ニュートン流体の流動挙動について，実験と数値解析の両面から研究を続けてきました．非ニュートン流体のような複雑な物質の流れのメカニズムを解明するためには，実験と数値解析の両面からのアプローチが有用です．今回は，非ニュートン流体の数値流動解析の中から，最近行っている流体内部構造に着目した流動解析について紹介したいと思います．その他の研究については，我々の研究室のホームページ（http://www-rheol.mech.eng.osaka-u.ac.jp/rheol-j.html）などをご覧下さい．

　多くの非ニュートン流体は，流体内部に原子・分子レベルよりも大きなスケールの構造をもっています．このような流体内部構造を有する流体は，複雑流体（complex fluids）とも呼ばれています．非ニュートン流体がもつ内部構造の例を模式的に書いたものを図1に示します．

 

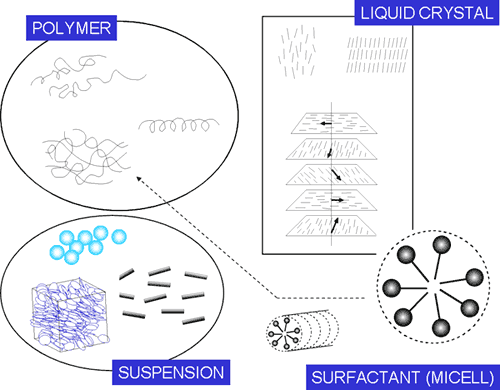
図１　非ニュートン流体（複雑流体）の内部構造の例

 

　非ニュートン流体の流動挙動やレオロジー特性を解析する際に，流動中の流体内部構造の変化は重要な要素のひとつとなります．非ニュートン流体の示す特異な流動挙動は，流体のもつ内部構造の変化と密接に関係があると考えられます．例えば，高分子流体（図1左上）の場合，柔軟に形態が変化する高分子の，流れ中の形態の変化や，高分子が絡み合ってできるネットワーク構造の変化は，粘度の非ニュートン性や弾性的性質の発現に関係し，高分子流体のマクロ流動挙動に影響します．液晶（図1右上）の場合には，剛直で棒状の液晶分子が配向し，ある種の秩序構造をつくります．液晶の配向方向や配向度は，液晶の流動特性や，液晶を利用した製品の機能に関係します．サスペンション（図1左下）では，液体に分散している粒子の配向や粒子が形成する構造が，流動挙動や流体の機能性に影響を及ぼします．また，分散する粒子の形状によって，流動挙動が大きく変化すると予想されます．界面活性剤中では親水基と疎水基をもつ界面活性剤分子がミセル（micell）と呼ばれる会合体（図1右下）を形成し，棒状や球状の形態をとります．さらにそれらがネットワーク構造を作り，高分子流体と同様に顕著な粘弾性を示すことも知られています．

　これまでの研究でよく用いられてきた数値解析では，流体の挙動を記述する構成方程式（constitutive equations）を，連続体力学の保存則から導かれる連続の式，コーシーの運動方程式，エネルギー方程式と連立させて，適切な初期条件，境界条件のもとで解くことによって，流れ場を求めます．ニュートン流体では，ニュートンの粘性則が構成方程式になります．

　非ニュートン流体の特異な流動挙動の記述は，構成方程式によるわけですから，非ニュートン流体の流動解析では，構成方程式が重要な役割を果たすことになります．粘弾性流体のひとつである高分子流体の構成方程式の場合，分子運動論的なアプローチから導出されるモデルがあります ^{(1, 2, 3, 4)}．例えば，ダンベルモデルがそのひとつです．

　高分子の力学的挙動を，2個の球をバネで連結したバネ－ビーズモデル（図2）で表し，多数のダンベルの配向や伸びの統計力学的な平均を用いて，高分子の寄与による応力を決定することができます．このとき，バネの特性としてフックの線形バネ（図2a）を考えると，上対流Maxwellモデルが導かれます．このモデルは，実際の高分子流体の特性を記述するためには不十分であり，より現実的なものとして，有限伸長性の非線形弾性バネ（図2b）を考えたモデル，FENE（Finitely Extensible Nonlinear Elastic）ダンベルモデル，があります．この場合，数学的に閉じた形の微分方程式を導くためには，何らかの近似を導入する必要があります．

　このように，平均量に関する微分方程式として構成方程式を導くことで，構造に関する詳細な情報は失われます．また，近似を入れることによって，実際の高分子流体の挙動を十分には表現できなくなることもあります．

 

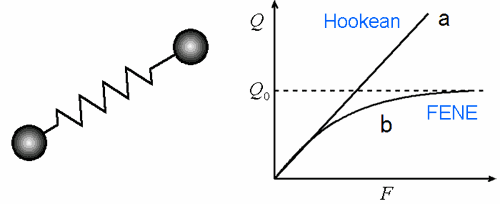
図２　バネ－ビーズモデルとバネの特性（バネの長さQと荷重Fの関係）

 

　一方，統計力学的な処理ができるほど多数のダンベルの挙動を，実際にシミュレーションし，アンサンブル平均を取ることによって，そのような近似を用いることなく解析を行う方法もあります⁽⁵⁾．応力場を，統計力学的手法によるシミュレーションの結果を用いて計算し，速度場や圧力場を，有限要素法などを用いたマクロ計算によって計算することにより，比較的複雑な流れ場の計算を行うアプローチは，CONNFFESSIT (Calculation Of Non-Newtonian Flows: Finite Elements & Stochastic Simulation Techniques) アプローチ⁽⁵⁾と呼ばれています．図3はFENEダンベルモデルに対して，平行平板間のスタートアップ流れを，統計力学的手法を用いて計算した結果 ⁽⁶⁾ の一例です．図では配向ベクトルの時間変化の様子を示しています．時間とともに配向ベクトルが定常状態へと変化する様子がみられます．

 

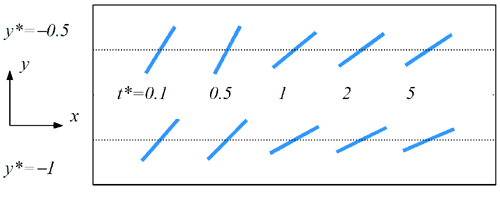
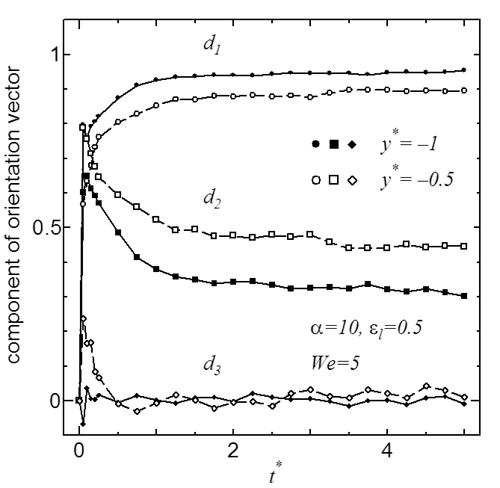
図３　高分子溶液（FENEダンベルモデル）の平行平板間のスタートアップ流れにおける配向ベクトルの時間変化

 

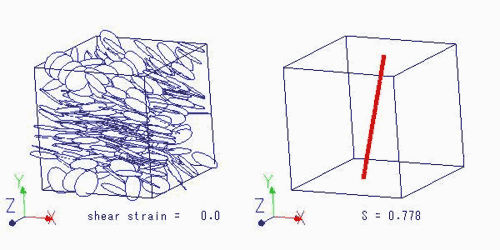
　流体内部構造をよりダイレクトに扱おうとした流動解析が，次のブラウン動力学シミュレーションによる解析です．図4は，ディスク状粒子分散系のせん断流れ中の流れ挙動をブラウン動力学（Brownian Dynamics; BD）シミュレーションにより解析したものです^{(7, 8)}．左側は流れ中の粒子の様子のスナップショットを，右側は粒子の平均的な配向方向を表すダイレクタを表しています．ダイレクタはディスク状の面に垂直な方向を示しています．図中のSは配向秩序度で，1に近いほど，粒子が同じ向きにそろって配向していることを意味します．

　この計算では，ディスク状粒子を扁平な回転楕円体で近似し，粒子間の相互作用を粒子間ポテンシャルによって表現し，さらにブラウン運動の効果をランダム力として取り入れています．周囲の境界条件に，周期境界条件を適用しています．ここでは，せん断流れを表すために，せん断変形の分だけ粒子の位置をずらす処理を行うLees-Edwardsの周期境界条件⁽⁹⁾を用いています．図4の結果は，基本セル内の粒子数が256個のものです．現在では基本セル内の粒子数をより多くしたものでシミュレーション結果⁽¹⁰⁾を得ていますが，ここでは，粒子の運動の様子が分かりやすいので，粒子数の少ないものの結果を示しておきます．図4の動画で，粒子の運動の様子と，粒子の平均的な配向方向を示すダイレクタの時間変化の様子をご覧頂けます．動画では，ダイレクタが連続的に回転するタンブリング（tumbling）や，ダイレクタが回転を躊躇するようなワギング（wagging）という挙動がみられます．

　このようなシミュレーションでは，構造の時間変化を調べることや，粒子の配置や配向をもとに応力を計算することにより系のレオロジー特性を求めることもできます⁽¹⁰⁾．実際に，シミュレーションをもとに求めたレオロジー特性は，実際のディスク状粒子分散系のレオロジー特性を表現することができました．また，そのような解析結果は，非ニュートン流体の特異なレオロジー特性の発現メカニズムの解析に有用なデータを与えます．

図４　せん断流れ中の円板状粒子の挙動のブラウン動力学シミュレーション
クリックすると再生： 10MB

 

　流体のミクロ構造を考慮した流動シミュレーションは，計算負荷も大きく，主として単純せん断流れなどの簡単な流れ場を対象としています．現状では，複雑な流れ場におけるマクロ流動挙動の解析や，工学的な応用を考えた場合，構成方程式を用いた解析がリーズナブルであると言えます．我々は，ミクロ構造を考慮した流動シミュレーションを，複雑な流れ場に適用し，実際の成形過程などで見られる複雑な流れ場での解析を目指しています．さらに，将来的にはシミュレーションにより，欲しい流動特性や機能を発現させるための流体のデザインも可能になってくるのではないかと考えています．

 

参考文献

1. Bird, R. B., Curtiss, C. F., Armstrong, R. C., Hassager, O., Dynamics of Polymeric Liquids, Vol. 2, Second Edition, (1987), John Wiley & Sons.
2. Larson, R. G., Constitutive Equations for Polymer Melts and Solutions, (1988), Butterworths.
3. Tanner R. I., Engineering Rheology, Second Edition, (2000), OxfordUniversity Press.
4. Owen, R. G., Phillips, T. N., Computational Rheology, (2002), ImperialCollege Press.
5. Öttinger, H. C., Stochastic Processes in Polymeric Fluids, (1996), Springer.
6. Yamamoto, T., Mori, N., Numerical Simulation of Viscoelastic Start-Up Flow between Parallel Plates Using Stochastic Calculation, JSME International JournalSeries B, 47 (2004), 1-8.
7. Yamamoto, T., Suga, T., Mori, N, Brownian Dynamics Simulation for Suspension of Oblate Spheroidal Particles in Simple Shear Flow, Slow Dynamics in Complex Systems, AIP Conference Proceedings, 708 (2004), 148-149.
8. Yamamoto, T., Suga, T., Mori, N., Brownian Dynamics Simulation of Flow-Induced Structure and Rheological Properties of Suspension of Oblate Spheroid Particles under Simple Shear, Proceedings of the XIVth International Congress on Rheology (CD-ROM), NF27 (2004).
9. Lees, A. W., Edwards, S. F., Journal of Physics C, 5 (1972), 1921-1928.
10. Yamamoto, T., Suga, T., Mori, N, Brownian Dynamics Simulation of Orientational Behavior, Flow-Induced Structure, and Rheological Properties of Suspension of Oblate Spheroid Particles under Simple Shear, Physical Review E　(in press).