流れ 2006年4月号 目次
― 特集:噴流の制御 ―
| リンク一覧にもどる | |
超音速ジェットからの放出される強い音波の抑制
 前川 博 広島大学大学院 |
1. はじめに
超音速ジェットから発生する騒音の抑制は,亜音速ジェットと比較して超音速ジェットからの騒音が極めて大きいことより,次世代超音速輸送機の開発においてキーテクノロジーの一つに上げられてきた.亜音速ジェットにおいて発生する音波の場合、ジェットせん断層の渦構造が主要な働きをすることが知られている.例えば単純化した円形層流ジェットにおける渦輪のペアリング運動からの音波発生はその典型的な例である.このように音源となる渦運動を制御対象として捉え,ジェットノズルにシェブロン形状が適用(実用化)された場合の成功例に見られるように,低速ジェットの場合の静粛化は発達するジェットせん断層を効果的に操作する方法を開発することが重要な課題であったといえるだろう.
一方,超音速ジェットから発生する音波はさらに複雑であるため,低速ジェットの静粛化技術の延長だけでは効果は大きくないと考えられてきた.超音速ジェットから発生する音波は,乱流せん断層から発生すると考えられてきたマッハ波と,衝撃波が関係するノイズ(Shock generated noise:これ以降,本文中ではショックノイズと呼ぶ)がある.適性膨張でない場合,ショックノイズはジェットプルームにおける衝撃波と乱流との相互作用によって発生する.また,ショックセルの間隔がジェットせん断層に対して最も成長する波動の整数比になると,ショックセルが振動してジェットスクリーチと呼ばれる極めて狭い周波数帯で高インテンシティのノイズが発生する.これら,衝撃波に関連するショックノイズは,実験により精力的に研究され80年代後半には静粛化の成果が現れた.その主な要因としてノズル形状を研究することでノイズ低減の対策ができたとされている.しかしながら,流体現象全般的に言える事であるが、乱流に関する研究の進展は遅く,超音速ジェットにおける騒音の問題でもそうであって,乱流せん断層内を超音速で移動する音源から発生すると考えられてきたマッハ波に関する理解はまったく不十分であった.超音速流れの乱流についての実験的研究にはいくつかの困難があることを考えると,乱流を理解するDNSの役割は益々重要になるであろう.また,DNSを使って超音速ジェットの制御のポイントを理解することは開発の重要なステップになると考えられる.
本稿では,そのマッハ波が発生するメカニズムを示し,そしてマッハ波を抑制する制御法の基となる流体力学の応用法を提案する.
2. 強い音波の放射機構(DNS結果(1))
平面ジェット(ジェットマッハ数Mj=2.4、対応する移流マッハ数Mc=1.17)上流から一様等方乱流場(図ではRandomと記述する)を導入した場合におけるジェットの発達の様子と一対の斜めモードをさらに加えた場合を比較した.ただし,速度勾配テンソルの第二不変量Qを使って渦構造を表現し,音響場は速度場の発散の等値面によって示した.ノズル出口速度分布の半値幅を代表長さとするレイノルズ数はRe=1000(ノズル長さを使うとRe=2000)である.ノズル出口近くではせん断層は遷移状態であり,Random撹乱の場合せん断層内に斜め渦(縦渦)があらわれていることが上から見た図と横から見た図によって観察することができる(図1参照).二つのせん断層の間はポテンシャルコアがあり,渦が発達して,下流ではポテンシャルコアが消失することがわかる.位相速度が亜音速の斜めモードを振幅2%としてRandom撹乱といっしょに導入すると,図2のように,せん断層内に斜め渦が早い段階で出現して,せん断層内の渦の発達(ラムダ渦)を促進して,Randomケースより早い段階でポテンシャルコアが消失することがわかる.そしてこの結果を,発生する音響場と重ね合わせてみると,図3に示すように,音響場はポテンシャルコア-が消失した場所から放射されているようにみえる.この結果は軸対称ジェット(移流マッハ数Mc=0.92)のDNS計算(2)と一致する。せん断層の発達に伴う速度変動エネルギーと音響場エネルギーの増減の相関を調べたことによって発生機構は次のように明らかになった。音波となるモードが増幅するためのエネルギーはせん断層から供給されるが,ポテンシャルコアが消失するとその供給が絶たれ,同時にその下流ではジェットから離れていくのでこのような強い音波がコア消失位置から放射されるパターン形成が行なわれたと理解することができる.ただし、マッハ数が大きいので、増幅されて発生した強い音波がジェット外側に伝播する圧力変動波面はすぐに急峻になる.

図1.Random撹乱(等方性乱流)を加えたジェットの構造(上面図と側面図:Q=0.1)

図2.Random撹乱(等方性乱流)に一対斜めモード撹乱を加えたジェットの構造(上面図と側面図:Q=0.1)
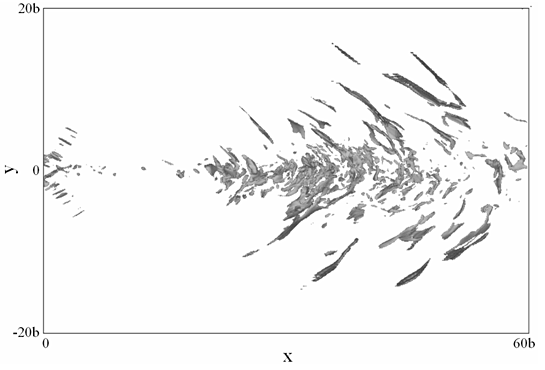
図3.音響場(速度場圧縮項(Divu=-0.05)):Random撹乱に一対斜めモードを導入した場合
3. 線形安定性解析の利用
低速ジェットにおける渦の合体のような非線形現象から音波が発生するのではなく,より線形的な発達の仕方をするのが超音速ジェットである.層流ジェットの場合に与えたMichalke(1965)(3)の考えをTamなど後の研究者が発展させた結果、超音速流れでのジェット騒音予測法の基本的枠組みは以下のように考えられている.流れ場を
![]()
のように平均と乱流乱れと決定論的な3つの成分で表し,乱流の効果を二次的に導入するものである.決定論的(Deterministic)成分については,明らかに層流の安定性理論と類似した線形方程式から得られる. 平均密度分布や速度分布そしてマッハ数が決まると決定論的成分は求められ,粘性の影響と同様に乱流の影響は二次的補正として受け取ってよいと考える.すなわち,音波発生を含む決定論的成分の空間増幅率に乱流せん断層発達係数を掛け合わせておく考え方である.線形安定解析から得られる圧力の固有関数を基本にしたモード展開の和が基本関数であるので,例えば音響インテンシティの大きい特定のストローハル数の成分について予測理論をあてはめると,軸対称乱流ジェットの場合ヘリカル第一モードが実験結果の全体的特徴をよくとらえていることが知られている.しかしながら,音波発生位置は実験と予測理論結果は一致しない.これは乱流現象を二次的に取りあつかったことがその原因で超音速ジェットせん断層の発達は乱流現象そのものだからである.軸対称ジェットプロファイルについて線形安定性理論で解析すると,第一ヘリカルモードの成長率は高次モードに比べて極めて大きく,さらにその位相速度は大きい.したがって,ジェットマッハ数が増加すると,明らかにその位相速度はまわりの空気の音速を超えることになり,急峻な圧力変動を導く重要な音源となることが容易に予想されるのである.乱流場を導入した軸対称ジェットの音響場(2)を観察すると,ヘリカルモードの対が発達した場合の特徴を示していることがわかる(同一半径上に交互に圧縮・膨張領域が現れ,それらが重なり合って圧縮・膨張領域が外側に伝播する音響場が観察される).
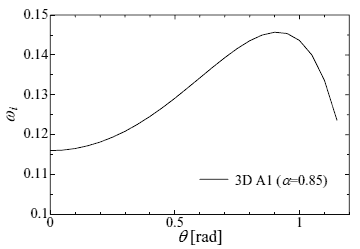
図4 ケルビン・ヘルムホルツ3次元モード(反対称モード)の成長率
したがって,急峻な勾配をもつ圧力変動の発生を抑える目的を達成するのにエネルギー供給時間を短くすることが重要である.そこで,亜音速の位相速度をもつ撹乱のうち、早く渦に発達しせん断層に有効な作用をすることが最も期待できる撹乱をさがした.安定性解析で見出された3次元斜めモードを図4に示す.図4の縦軸は成長率を表し,横軸は主流方向となす角度である.不安定モードの中でケルビン・ヘルムホルツ反対称モード(A1)の最も成長率が大きな場合は位相速度が亜音速であることがわかる.この斜めモードを一対組み合わせて撹乱として与えた結果を示す.音響場をRandom撹乱の場合と比較すると,Random撹乱の場合発生する二次元的な強い音波であるが、斜めモードを組み合わせると発生段階から波面が3次元的になっている様子が観察された。Random撹乱のみ導入すると急峻な二次元的勾配をもつ圧力波が多く存在するため、図5に示すように、スパン方向に平均してもまだ変動勾配は急である.一方、斜めモードを導入した場合は発生した圧力変動がより3次元的であり、ジェット下流(x=55b)のジェット外側(y=15b)では圧力変動には急峻な勾配がみられなくなっている.また,圧力の全変動についてジェットから離れた位置(10<y/b<40)でSPL(dB)を比べて見ると音波としての強さがy/b=40で5dB弱小さくなっていることが認められる(図6).
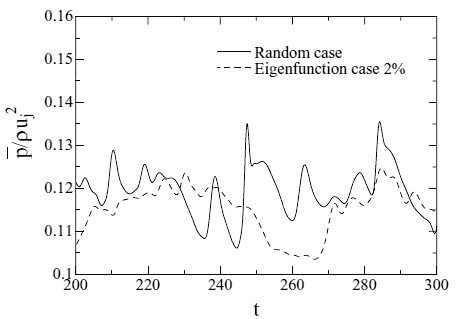
図5 圧力変動p(スパン方向平均)の時系列データ(x=55b,y=15b)
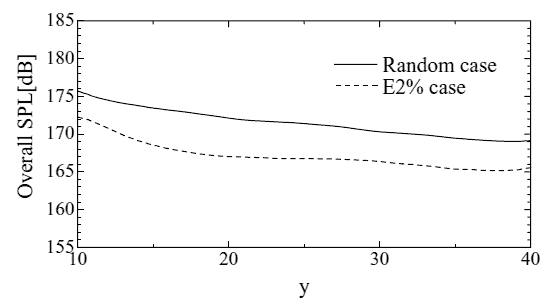
図6 遠方場に向かっての音響場減衰の比較
4. まとめ
超音速平面ジェットからの音波発生機構についてDNSを使って示した.大きな振幅に発達する低周波音響成分はせん断層の発達とともに成長し,その放射はジェットポテンシャルコアが消滅する位置付近で起こる.線形安定性解析では成長するモードの中で位相速度が超音速になるモードがいくつかある.平面ジェットでは伝播方向が主流と成す角度が小さな反対称モードであり、円形ジェットでは第一ヘリカルモードの位相速度が超音速になる.それらの成長を抑制することが超音速ジェットの静粛化に重要である.
位相速度が亜音速で成長率が大きい一対の斜めモードをジェット入り口に導入することによって,ラムダ渦がジェットせん断層の発達を促進して,大きな強さをもつ音波へのせん断層からのエネルギー供給をできるだけ抑えることができることをDNSで示した.参考文献

