流れ 2009年12月号 目次
― 特集テーマ: 未来を拓く超音速機 ―
| リンク一覧にもどる | |
自動車用ターボチャージャの一部を用いたターボポンプの実験的研究
野末 辰裕、
|
1.緒言
微小重力(μG)下の実験のため、100 kg程度の実験装置に数分以上の実験時間を低コストで提供する手段として再使用型小型ロケットがあり、我々は、垂直(鉛直)上昇/降下、単段(single stage)のタイプにつき検討を行っている。昨年度までの検討で求めたロケットの形状、仕様を図1、表1に示す[1]。このロケットの特徴はエンジンにLOX(液体酸素)/LNG(液化天然ガス)を用いた点にあり、検討のベースとしたエンジン性能を表2に示す。また、ロケットの低価格化の一環として、このエンジンのキーコンポーネントであるターボポンプに自動車用ターボチャージャの一部を用いることを検討しており、その第1段階の実験的研究を行ったので報告する。
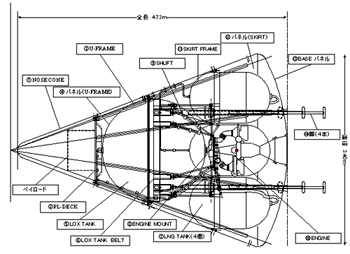
図1 ロケット概念図
表1 ロケット諸元
|
エンジン1基 |
寸法 |
3.4mφ×4.73mL |
重量 |
5,000kg (Wet, at launch) |
表2 エンジン諸元
| 推力 | 78.4 kN(真空) |
比推力 |
306 sec (真空) |
推進剤 |
LNG/LOX |
混合比 |
3.1:1 |
燃焼圧 |
3.5 MPa |
2.ターボポンプの設計
ロケット用ターボポンプは、推進剤をロケットエンジン燃焼室に供給する装置で、動力源は燃焼ガスである。表3にターボポンプへの要求を示すが、LOX用の方が厳しいので、これを目標とする。なお、ターボチャージャのタービンは約650℃以上の排気ガスで駆動されるが、この条件は燃焼室から抽出するガスを駆動源とするロケット用と同様である。しかし、ターボチャージャがコンプレッサでエンジンに供給する空気を圧縮するのに対し、ロケット用はポンプで極低温液体推進剤を昇圧し、燃焼室へ供給する。従って、タービン部分はターボチャージャのものを用い、コンプレッサの代わりに液体用ポンプを設計、取り付けることとした。表3に示すパワーを得るため、ターボチャージャは大型のトラック、バス用のものを選定し、計算の結果、使用回転数は65,000rpmとなった。この回転数は、通常のターボチャージャ(100,000rpmのオーダー)よりは小さいものの、通常の液体用ターボポンプの回転数よりはるかに大きいため、これに対応するポンプ、インペラの設計と実験による確認を行った。表4にインペラの形状につき示す。
表3 ターボポンプ要求
|
表4 インペラ形状
|
|||||||||||||||||||||||||||||||||||||||
3.実験
上記のターボポンプの危険速度把握のため「無負荷回転実験」を、ポンプ特性把握のため「水流し実験」を行った。
3.1 無負荷回転実験
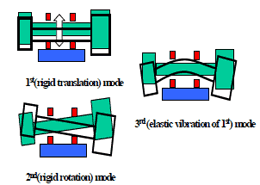
タービン、シャフト、インペラからなる回転部分が軸受けによって2点支持されて回転する系を、伝達マトリクス法によりシミュレーションした。このとき回転は無負荷(ポンプに液体のない状態)とし、回転部分単独の特性はインパクトハンマーで事前に計測した。しかし、軸受けのばね定数は不明なため、種々の値について実施した。求められた振動モードを図2に、固有振動数を表5に示す。この軸受けのばね定数を実験で求めるため、電動モーターで回転部分を回転させて振動特性を求める実験を行った。図3に実験の様子を、図4に実験結果を示す。図4で、位相が-90°ずれる点が、9,000rpm(150Hz)付近で見られることから、この回転数で1次の共振が発生していることが分かる。また表5で、ばね定数が10,000,000N/mのとき、1次の固有振動数が152Hzと実験で得られた値に近いことから、ばね定数はこの値であること、および、表5に示された2次(400Hz=24,000rpm)、3次(1,382Hz=82,920rpm)の固有振動数の値が推定される。2次は、次に述べる水流し実験の範囲であるが、実験に影響を与える共振は見られなかった。3次は、運用の回転数(65,000rpm)を超えた値である
 |
 |
||||||||||||||||||||||||
図2 振動モード |
図3 無負荷回転実験状況 |
||||||||||||||||||||||||
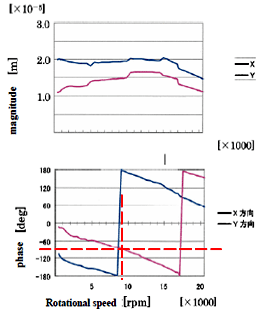 |
表5 固有振動数
|
||||||||||||||||||||||||
| 図4 実験結果 |
3.2 水流し実験
3.2.1 実験方法
ポンプに連続的に水を供給するため、ポンプを含めた水循環路を製作した。また、タービンの回転数を目標の65,000rpm程度まで高速に駆動するには、大容量のガス源が必要になり、東京大学柏キャンパス極超音速エンタルピー風洞(燃焼風洞)を用いて実験を行った。図5に実験装置のブロックダイヤグラムを、図6に実験の様子を示す。
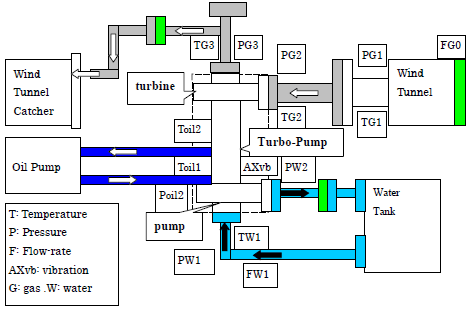
図5 ブロックダイヤグラム

図6 水流し実験状況
3.2.2 実験結果
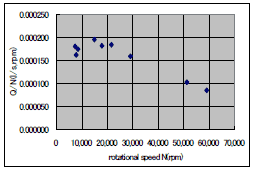
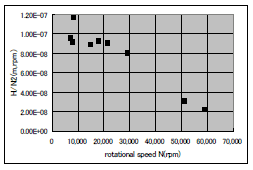
図7、図8に、以下の式で求めた、各回転数(N)における流量係数(Q/N)と揚程係数(H/N2)の結果を示す。
Q/N=流量Q(l/s)/N(rpm)、H/N2=揚程H(m)/N(rpm)2
両係数ともに、約22,000rpm(正確には21,540rpm)より大きなデータで減少傾向が見られる。
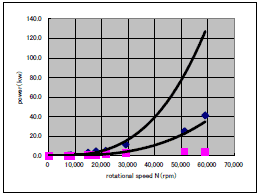
図9に、以下の式で求めた、タービン入力パワー(Pwrt-i)及び、ポンプ出力パワー(Pwrp-o)を示す。
Pwrt-i = G・(κ/(κ-1)・R・Tin・(1-π^(1-κ)/κ)
G:ガス質量流量(kg/s)κ: 比熱比 =1.4 R:空気のガス常数 Tin: タービン入口温度 (K)
π: 圧力比(=タービン出口圧/入口圧)
Pwrp-o= Q・(Pout-Pin)
Q: 流量 (m3/s) Pin: ポンプ入口圧 Pout: ポンプ出口圧
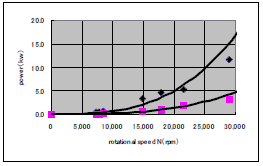
図9に示した2本の近似曲線は、それぞれ、21,540rpm以下のデータから最小自乗法で求めた、3次曲線(y=aN3)である。また、図9-aは図10の30,000rpm以下の範囲を示したものである。ここでも21,540rpmより大きなデータで曲線からの乖離が見られるが、回転数が大きくてもパワー、流量、圧力が小さいことから、キャビテーションが発生した空回りの現象が推定できる。
図13に以下の式によるキャビテーション係数(k)を示すが、揚程係数(縦軸)の減少傾向からも、キャビテーション限界が見られる。
k=(Pins-Pv)/((1/2)ρw・V2)
Pins: ポンプ入口静圧(絶対圧) Pv: 水の飽和水蒸気圧 ρw: 水の密度
V: ポンプ入口で水とインペラ先端の相対速度
表6に今回の実験結果と評価を示す。キャビテーションの発生しない範囲でも、流量係数、揚程係数は目標の約70%であった。評価の列では、回転数65,000rpmとし、結果の列の流量係数、揚程係数を用い、流量、ポンプ昇圧(Pout-Pin)、ポンプ出力パワー(Pwrp-o)を計算したが、目標の54%であった。なお、キャビテーション限界が今後、k=0.04まで改善できるとして、この係数となるポンプ入口圧を設定した。
 |
 |
||||||||||||||||||||||||||||||||||||||||
| 図7 流量係数 | 図8 揚程係数 | ||||||||||||||||||||||||||||||||||||||||
 |
 |
||||||||||||||||||||||||||||||||||||||||
| 図9 タービン/ポンプパワー | 図9-a タービン/ポンプパワー | ||||||||||||||||||||||||||||||||||||||||
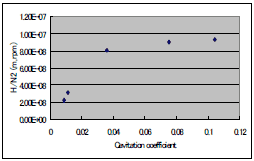 |
表6 実験結果と評価
|
||||||||||||||||||||||||||||||||||||||||
図10 キャビテーション係数 |
|
4.結論
自動車用ターボチャージャの一部を利用した、LNG/LOXロケットエンジン用のターボポンプを設計し、実験と解析で評価した。この第一段階の、無負荷回転実験と水流し実験を実施した。
5.参考文献
| [1] | 第52回宇宙科学技術連合講演会 講演集1J14 2008:マイクログラビティ実験用ロケットの概念検討 |





