流れ 2015年11月号 目次
― 特集テーマ:2015年度年次大会(その1) ―
| リンク一覧にもどる | |
流体機械内部流れ最適化の変遷と近未来への展望
後藤 彰
|
1. まえがき
ポンプ,圧縮機,ファンといった流体機械は,我々をとりまく様々な機械システムの「心臓」の役割を果たすことから,高い堅牢性と信頼性が求められる.また,エネルギー変換機械である流体機械には,環境負荷低減の観点から常に高い効率が求められる.こうした背景から,長年に亘り流体性能の改善研究が実施されてきた.1990年代から本格化した産業界でのCFD(Computational Fluid Dynamics)の活用は,複雑な3次元内部流動の解明に大きな貢献を果たし,その更なる高精度化への期待は大きい.しかし,解析の究極の目標が実験代替である反面,流体機械内部流れの実験研究には100年以上の歴史があることを鑑みれば,「解析技術」の高度化への取り組みだけでは不十分であり,「設計(最適化)技術」の高度化への取り組みが流体機械の画期的改善に必須であることが理解できよう.以上を背景とし,流体機械最適化技術の変遷を俯瞰し,今後の方向性を論じる.
2. 設計技術の変遷
図1に,筆者の所属先における解析技術の進歩と,設計技術の進歩を示す.1970年代までの設計は熟練設計者の知見に基づく線図設計に依存していたが,RANS-CFD技術の実用化(1)に続き,1990年代には二次流れなどの複雑な内部流動を制御・最適化する手段として3次元逆解法技術が確立された(2).同技術によれば,流体挙動に直結する羽根負荷分布を入力として,少ない設計パラメータで3次元の複雑な自由曲面の翼面をごく短時間に生成できる.2000年代前半には3次元逆解法と数値最適化を組み合わせた単目的の自動最適化が提案され (3),計算機の進歩と相まって,2010年前後には多点・多目的最適化へと展開された(4).産業界で課題となる最適化問題の大半は,多目的で学際的な(複数の技術分野にまたがる)性格を持っており,今後は,多目的・多領域最適化技術の実用化が重要となる.
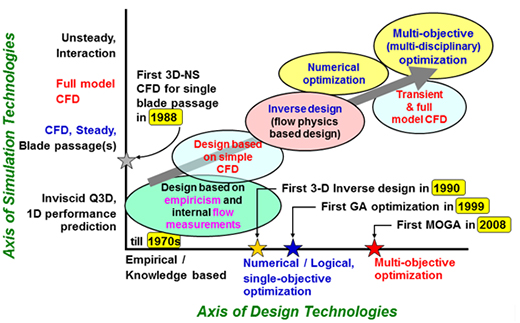
Fig.1 History of simulation and design technologies.
3. 数値最適化事例とその課題
3・1 多目的最適化
産業界が直面する最適化問題の大半は,複数の目的関数を持つ多目的最適化である.例えば,探索的な多目的最適化アルゴリズムであるMOGA(Multi-Objective Genetic Algorithm)を用いれば,他の目的関数を劣化せずには,どの目的関数も向上することができない解である「パレート解」が得られる.すなわち,多目的最適化問題の解は,こうしたパレート解空間の中で目的関数間のトレードオフ選択を行う事に帰着する.図2は,斜流ポンプの性能特性最適化問題(4)の事例で,①高効率,②低締切り揚程,③性能安定性,④低締切り動力という4つの目的関数が扱われている.MOGAにより得たパレート解空間を,例えば図2(c) に示すように2-D空間に投影すれば,二つの目的関数間のトレードオフ選択が行える.しかし,4個の目的関数間のトレードオフ関係を可視化することは困難である.図3は,こうした課題に対し,4つの目的関数間の関係を自己組織化マップ(5)により可視化した事例を示す.多目的最適化では,こうした最適解探索や設計選択を支援するための可視化技術も重要になる.
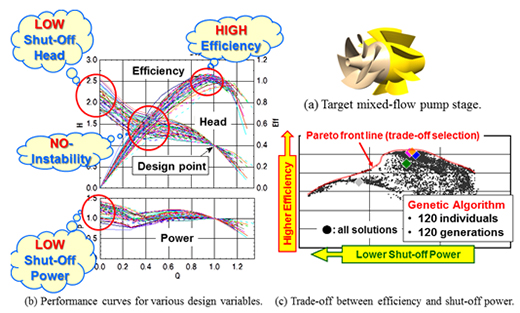
Fig. 2 Multi-objective optimization of mixed-flow pump performance curves.
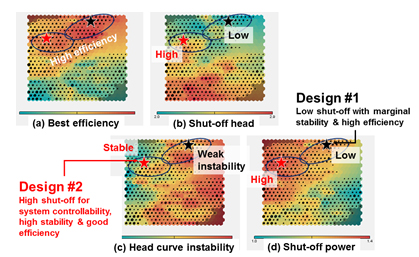
Fig. 3 Trade-off selection for 4 design objectives using SOM (Self-Organizing Map).
産業界では,流体・構造強度・振動といった,複数の技術分野にまたがる多領域最適化問題に遭遇することが多い.そうした課題を,解析技術だけに依存し,力づくで解くことは実用的でない.図4は,高吸込み性能を有する高速ポンプの設計において,形状生成に3次元逆解法,吸込み性能の目的関数に低圧力の範囲(経験的指標1),構造強度の目的関数に羽根車強度に最も影響する羽根スイープ角度(経験的指標2)を採用し,ごく短時間で多領域最適化を実施した事例である.圧力場はポテンシャル理論でも精度よく求まることから,ポテンシャル理論に基づく3次元逆解法だけを使用し,CFDやFEMなどの数値解析は用いていない.つまり,「物理的な示唆」の下で,的確な目的関数と適切な解析技術を如何に選択するかが,設計現場で多目的・多領域最適化を効率的に運用するための鍵である.
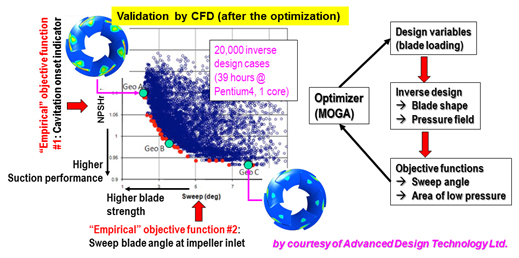
Fig. 4 Multi-disciplinary optimization using empirical knowledge for design objectives.
3・2 複雑流路の最適化
流体機械の流路は,複雑な3次元形状を有する部分が多い.そうした形状の定義には3次元CADのパラメトリック設計が用いられるが,複雑な形状を表現するために設計変数が膨大となり,実用的な時間で最適化問題を解くことは難しい.図5はそうした課題に対し,勾配法をベースとしたadjoint最適化設計(6)を適用した事例を示す.両吸込みポンプの吸込みケーシング(図5(a))を対象とし,目的関数(損失低減と出口流れの一様化)に関するadjoint感度解析を行い,形状変更のベクトルを導出して(同図(b))形状最適化を実施し,出口に存在していた剥離渦(同図(c))を大幅に緩和した(同図(d)).この方法では,解析メッシュ点すべてを設計変数にでき,かつ解析時間も通常のCFD解析程度に抑えられるため,自由度の高い形状最適化が実用的な時間内に実現できる.なお,adjoint感度解析によれば形状最適化のための様々の有益な「物理的示唆」を得ることもできる.
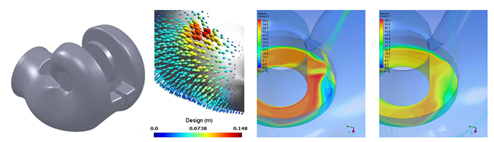
(a) Suction chamber model (b) Sensitibities (c) Original design CFD (d) New design CFD
Fig. 5 Optimization of a double suction chamber for a centrifugal pump.
4. あとがき
市場のニーズ変化に追随し,付加価値の高い流体機械をタイムリーに創出していくには,CFDに代表される数値シミュレーション技術の高度化に加え,多目的・多領域の最適化などによる設計技術変革へのチャレンジが必要である.産業界が直面する複雑で学際的な課題に効率的に対処するには,経験則との組合せや,制御対象となる物理現象をより低近似で表現するシミュレーション技術の選択も重要である.
すなわち,近未来において流体機械の製品イノベーションを目指すための最適化技術では,①市場の声などに基づき製品コンセプトを構築し,②そのプロトタイプに対する詳細な実験・数値解析検討を行い,対象とする物理現象に影響を与える設計変数に関する「物理的示唆」を獲得し(例えば,圧力勾配を制御し二次流れを抑制する),③それをできるだけ低次の近似で再現する予測手法(経験則を含む)を選択し(例えば,ポテンシャル理論で圧力場を予測),④的確に最適化問題を構成した上で設計空間を定義し,⑤大域的な探索を可能とする最適化アルゴリズムによる最適化を実施し,⑥得られた目的関数空間を可視化し,迅速な設計選択を実現することが重要である.図6にこうした最適化プロセスのイメージを示す.
ディジタルエンジニアリングを活用する若い世代が,数値最適化技術の研究・応用に取り組み,製品イノベーションや業務プロセス変革に継続的に貢献することを期待したい.
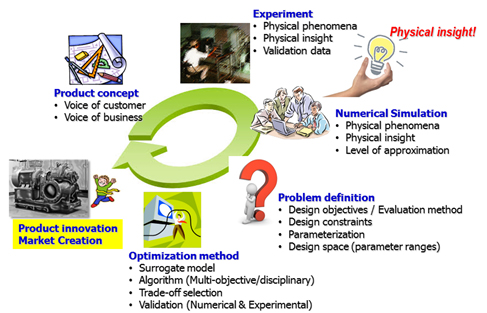
Fig. 6 Image of workflow for product innovation.
引用文献


