流れ 2018年3月号 目次
― 特集テーマ:第9回日韓熱流体工学会議(TFEC9) ―
| リンク一覧にもどる | |
平板上の遷移境界層における乱流の始まり
福西 祐
|
1. 緒言
平板境界層の遷移過程では,これまでにも特徴的な流れの構造が報告されてきた.主流乱れが小さい時には,2次元的なT-S波が線形成長した後に3次元化し流れ場は乱流になる.その際にはΛ渦と呼ばれる渦が現れる[1].また主流乱れが大きい場合には,高速・低速の領域がスパン方向に並ぶストリーク構造が現れ,それが不安定化してヘアピン渦や準縦渦(quasi-streamwise vortices)と呼ばれる渦が観察される[2].また孤立撹乱による遷移においても,乱流斑点の直前に現れる特徴的な渦構造[3]や小さいエネルギーで乱流を引き起こす最適撹乱[4]が報告されており,乱流遷移に関わる流れの構造に関する知見は数多く取り溜められてきた.
しかし,いざ“乱流が生まれるにあたって決め手となる渦構造はなにか’’と問われると,その答えは未だにない.本研究は乱流発生の鍵となる渦構造を特定することを目的としており,数値計算を用いて平板境界層の乱流遷移過程の最初期に現れる渦構造について調べたものである.噴流を短時間噴射することで境界層内に孤立撹乱を導入し,その噴射速度をわずかに変えることで最終的に乱流化する流れ場と層流に戻る2つの流れ場を得てそれらを比較することで,最終的には大きな違いを作り出すきっかけとなる渦構造を探し,流れ場の乱流化を引き起こす鍵とは何かを探った.
2. 低速ストリークの脇からの短時間噴射による乱流遷移の場合
境界層の乱流遷移において流れが乱流化する上流でしばしばストリーク構造が現れる.過去の研究においてストリーク構造は2つの不安定モードを持つことが示されており,このことはストリーク構造がBlasius境界層と比べて乱流になりやすい環境を提供しているものと考えることができる.本研究ではまず予備計算として,境界層内部に物体列を置いてその下流に定常なストリーク構造を形成させ,その後の主計算において低速ストリークの1つに対して短時間噴流を噴射する数値計算を行った.その際,噴射孔の位置を最も低速となる位置から多少ずらすことで,低速ストリークの位置に対して非対称な撹乱を導入することを試みた.これは低速ストリークの持つ2つの不安定性の内,より不安定が発現しやすい非対称モードの刺激を狙ったものである.
本研究では,一様流速で無次元化された噴流の噴射速度νjetを0.08及び0.10と設定した.νjet = 0.08の場合には,境界層内部に導入された孤立撹乱は減衰して層流状態へと戻ってしまうのに対して,νjet = 0.10の場合には撹乱が成長し,最終的には乱流状態となる.図1にそれぞれの条件下における渦構造の時間変化を示す.渦領域は速度勾配テンソルの第二不変量であるQ値を用いてQ = 0.001の等値面内部と定義し,回転方向を示すためにその表面を流れ方向渦度ωxで色付けした.まず,いずれの場合も噴射を短時間行ったことで境界層内に縦渦Aが形成される.νjet = 0.08の場合にはこの縦渦Aが時間の経過とともに減衰し流れ場は層流へと戻ってしまうのに対して,νjet = 0.10の場合にはt = 120において縦渦Aの上流側に新たに縦渦Bが現れ,さらにt = 180には成長した縦渦Aの下流と縦渦Bの上流に新たな渦が生まれ,次々と流れ方向に渦度の符号が反転した縦渦が並ぶ準縦渦列が形成される.そして最終的に境界層は乱流状態に至る.このような縦渦列は遷移境界層中において低速ストリークの非対称不安定モードが成長した結果現れる特徴的な構造である[2].
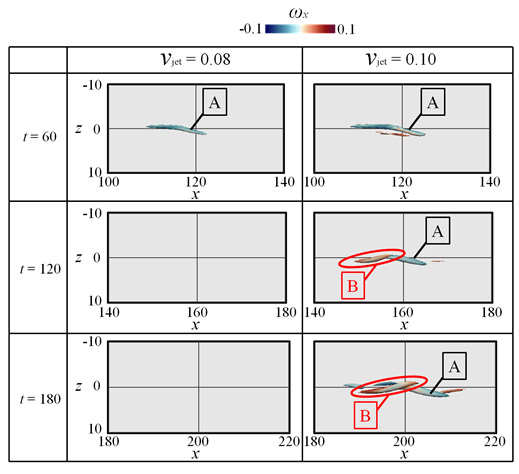
Fig. 1 Time variations of vortical structures. νjet = 0.08 and 0.10 cases compared.
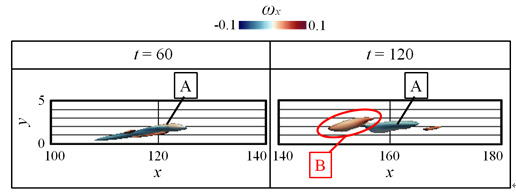
Fig. 2 Side views of vortex A at t = 60 and vortex B at t = 120.( vjet = 0.10 case)
縦渦A単独では乱流に至らないのに対して,νjet = 0.10の場合における縦渦Bの生成が流れ場が乱流へと至る鍵となっていることが分かったため,次に縦渦AとBの間にどのような違いがあるのかを探った.図2にνjet = 0.10の場合のt = 60における縦渦Aとt = 120における縦渦Bの側面図を示す.ここで縦渦のx-y平面内のx軸に対する傾きに着目する.t = 60における縦渦Aの傾きを求めるとΔy/Δx = 0.11となる.同様にt = 120における縦渦Aの傾きを求めるとΔy/Δx = 0.20となり,縦渦Bは縦渦Aと比べてx軸に対してより大きな傾きを持っていることが分かる.このことは,縦渦Bが境界層の持つ速度勾配によって伸長され,渦度がより大きくなる性質を持つことを示唆しており,この性質ゆえに乱流を引き起こす鍵となった可能性が高い.
図3に渦Bが生成されたt = 80のy-z平面における速度ベクトル場を示す.図中のカラーマップは流れ方向渦度ωxを示しており,黒線は渦Aと渦Bに対応するQ = 0.0005の等高線である.渦Bの下流部が渦Aに伴う旋回する流れによって巻きとられるようにして渦Aの上部へと移動している.これにより渦Bのx軸に対する傾きが大きくなり伸長されやすい形態を得た理由であると考えられる.
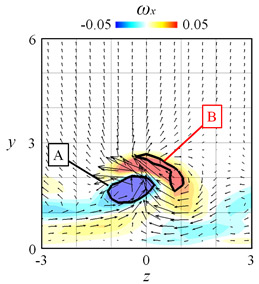
Fig. 3 Velocity vector field with color map of streamwise vorticity in y-z plane at t = 80.
3. 低速ストリークの中央へ短時間噴射した場合とストリーク構造がない場合における乱流遷移の鍵となる渦構造
最後に流れ場を変え,低速ストリークの最も低速となる位置から噴流を短時間噴射した場合と,ストリーク構造のないBlasius境界層に対して噴流を短時間噴射した場合についても乱流遷移の鍵を握る渦構造を特定した.図4に鍵となる渦構造を赤い楕円で囲んで示す.これらの図においては,見やすくするために図のアスペクト比が変更されているが,いずれの場合においても側面図を見ると乱流遷移の鍵となる渦構造はx軸に対して傾いた縦渦の形を取っており,この形態こそが乱流遷移を引き起こすきっかけとなる渦構造特有の特徴であることが示唆された.
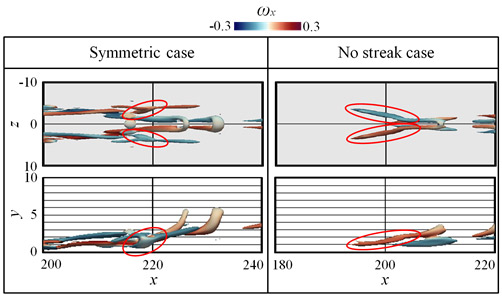
Fig. 4 Key structures in laminar-turbulent transitions.
Symmetric blowing case and no streak case.
4. 結言
乱流生成の鍵となる渦構造を探ることを目的として,ストリーク構造のある境界層におけるその低速部の脇,低速部の中央,そしてストリーク構造のない境界層に対して噴流を短時間噴射し,乱流化する場合と層流状態へと戻る2つの流れ場を比較し,それぞれの流れ場における乱流化の鍵となる構造を特定した.いずれの流れ場においても鍵となっていた渦構造は,x軸に対して傾いた縦渦という形態をとっており,これが乱流化の過程において重要な役割りを担う渦構造の特徴であることが示唆された.
5. 参考文献


