流れ 2018年3月号 目次
― 特集テーマ:第9回日韓熱流体工学会議(TFEC9) ―
| リンク一覧にもどる | |
PM2.5の帯電状態測定のための平行平板粒子分級器の数値シミュレーション
 |
 |
 |
 |
| 米道 卓音 慶應義塾大学 |
深潟 康二 慶應義塾大学 |
藤岡 謙太郎 慶應義塾大学 |
奥田 知明 慶應義塾大学 |
1. はじめに
第9回日韓熱流体工学会議(TFEC9)において講演発表を行い,光栄にも優秀講演表彰を頂いた.また,ニュースレターとして研究を紹介させていただく機会を頂いた.この場を借りて日本機械学会流体工学部門の皆様に御礼を申し上げる.本ニュースレターではTFEC9における講演発表の内容である,PM2.5の帯電状態測定のための平行電極板型分級デバイスの数値解析について紹介させて頂く.
2. PM2.5の帯電状態の測定
PM2.5をはじめとする空気中の微粒子は,呼吸によって人体に侵入し,肺などの呼吸器官に沈着することによって健康被害を引き起こすことが知られている.こうした悪影響を低減するために粒子の呼吸器官への沈着に関する研究が行われてきた.その中でも,粒子の帯電状態は呼吸器官への沈着量に大きく影響を及ぼすことが示されており,粒子が帯電している場合には帯電していない場合と比較して沈着量が増加することや(Cohen et al., 1998; Ali et al., 2008),帯電量の増加と共に沈着量が増加することが報告されている(Majid et al., 2011).また,粒子の帯電状態は粒子自身の発生原因によって変化することが報告されており(Forsyth et al., 1998; Ahn et al., 2001; Marra et al., 2008),空気中の粒子の発生源を特定する手がかりになると考えられている.
空気中の粒子の帯電状態に関する知見として,フィルター上に捕集した粒子層の正味の帯電量や表面電位の測定の報告(Okuda et al., 2015a)などがあるが,より直接的に健康被害に関わる個別粒子の帯電状態の解明には至っていない.そこで,奥田ら(2015b)は粒子を帯電状態ごとに分類し,個別粒子の帯電状態の測定を行うため,図1に示す平行平板粒子分級器を開発した.
図2にこの分級器内部および分級器を通過し,分級される粒子の模式図を示す.このデバイスは入口部,分級部,出口部の3つのセクションから構成されている.入口部中央の流路(Inlet 2)からはPM2.5などの微粒子を含んだエアロゾルが流入し,左右の流路(Inlet 1, Inlet 3)からはフィルターを通した清浄空気が流入する.中央の流路から流入した粒子は,分級部に誘起された電場によって主流垂直方向のクーロン力を受け,正負どちらかの電極へ向かって移動しながら下流へと流れる.この移動量や移動方向は粒子の帯電状態に依存しているため,3流路に分岐する出口部の各流路においてそれぞれ帯電状態ごとに分級された粒子を取り出すことができる.しかし,この主流垂直方向への移動量,移動方向から予想される流路とは異なる流路からの粒子の流出や,左右の出口(Exit 1, Exit 3)から流出する粒子に偏りが生じるといった問題点が実験結果から指摘されており,こうした問題点を解決することによる実験精度の向上が求められている.
そこで本研究では,これらの問題点の原因を数値解析によって明らかにすること,より高精度な測定を行える条件を求めることを目的とした.

Fig. 1 The parallel plate particle separator developed by Okuda et al. (2015a).
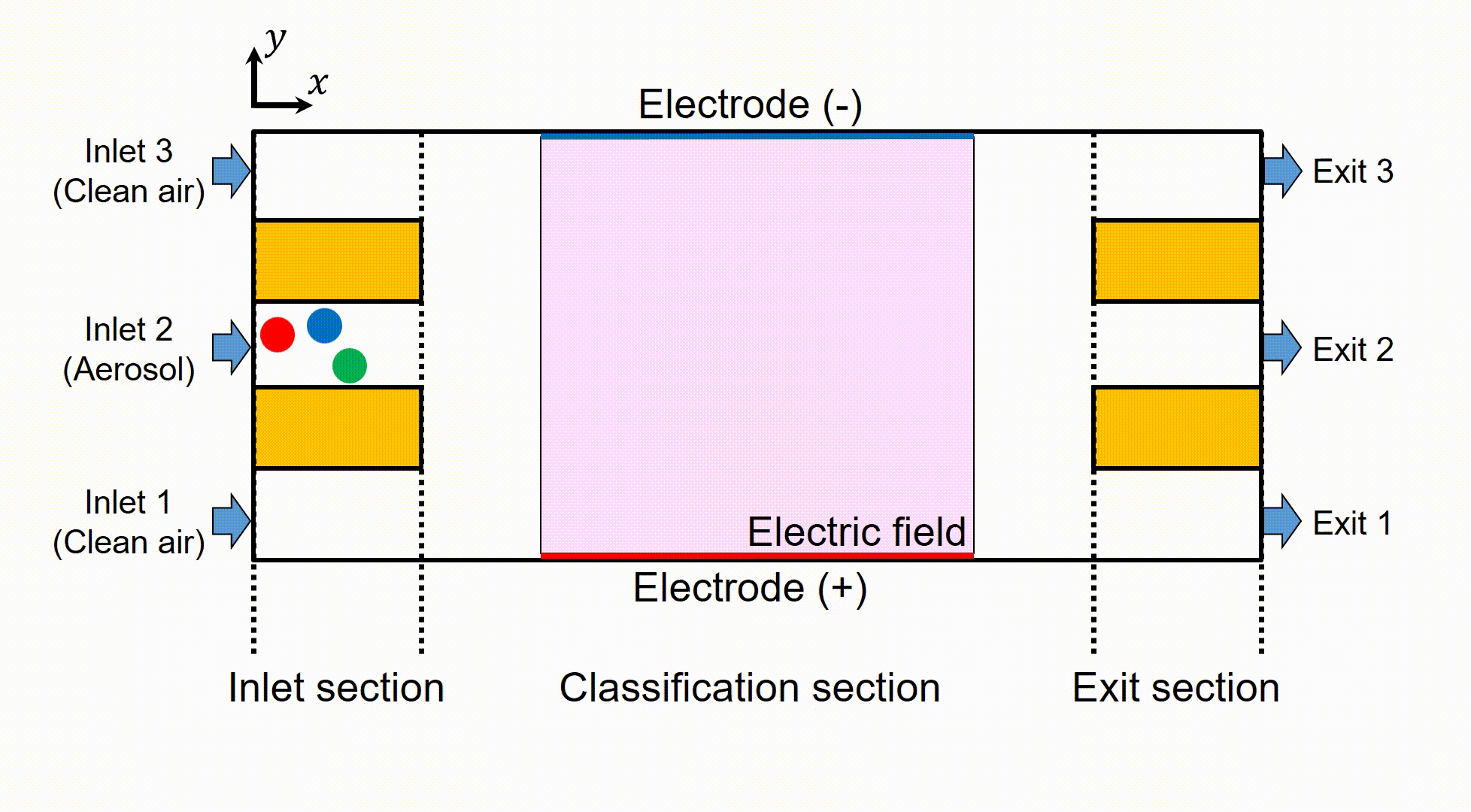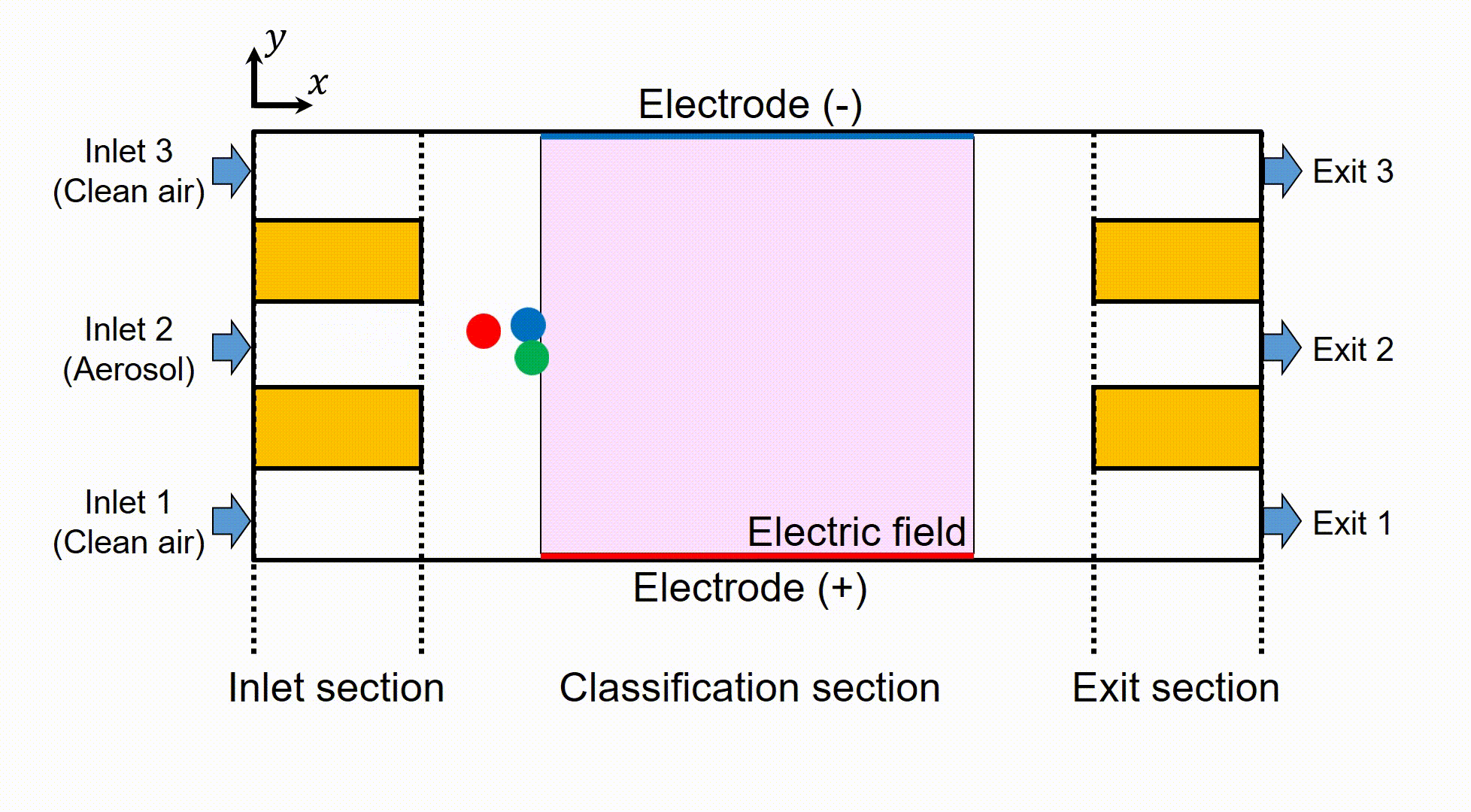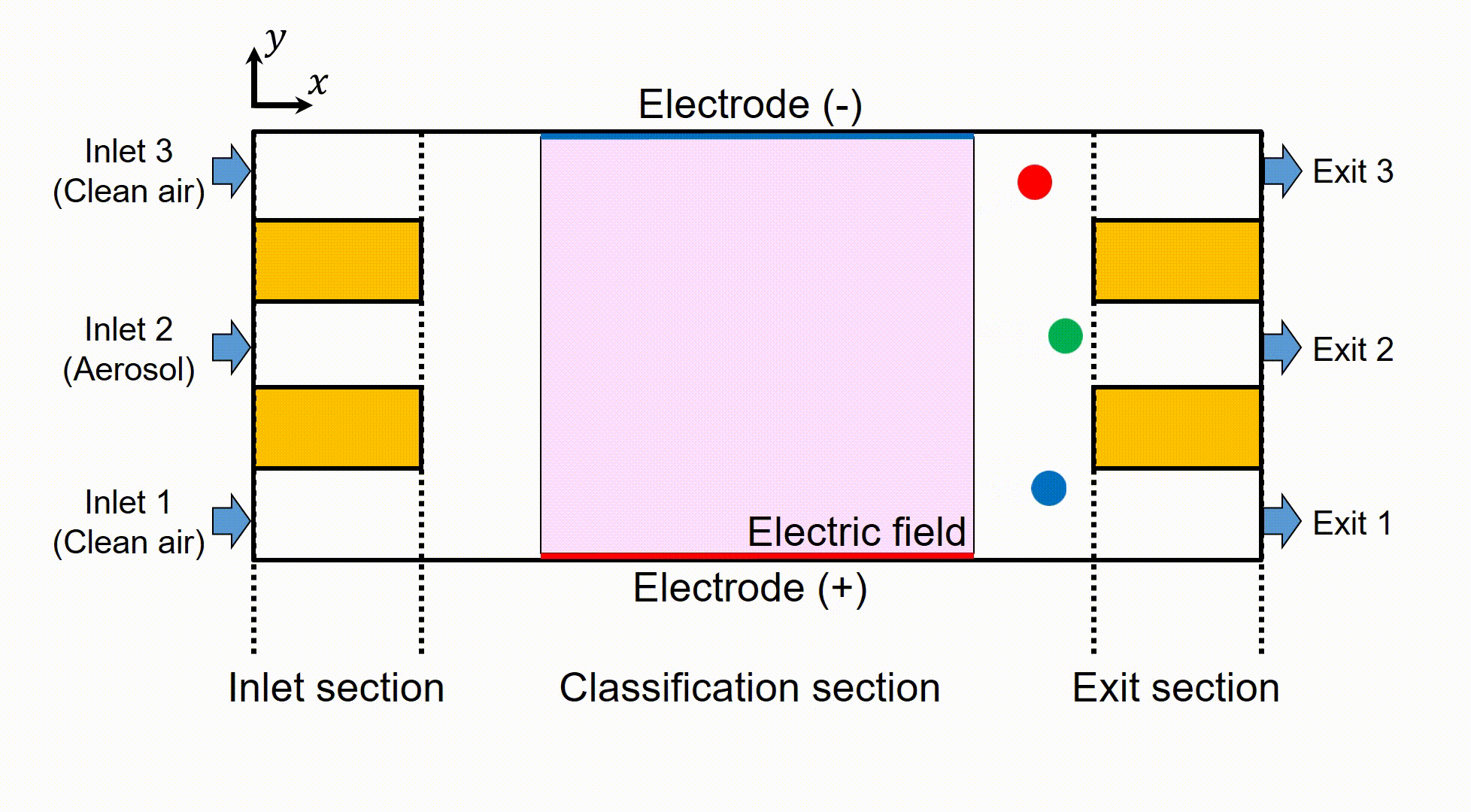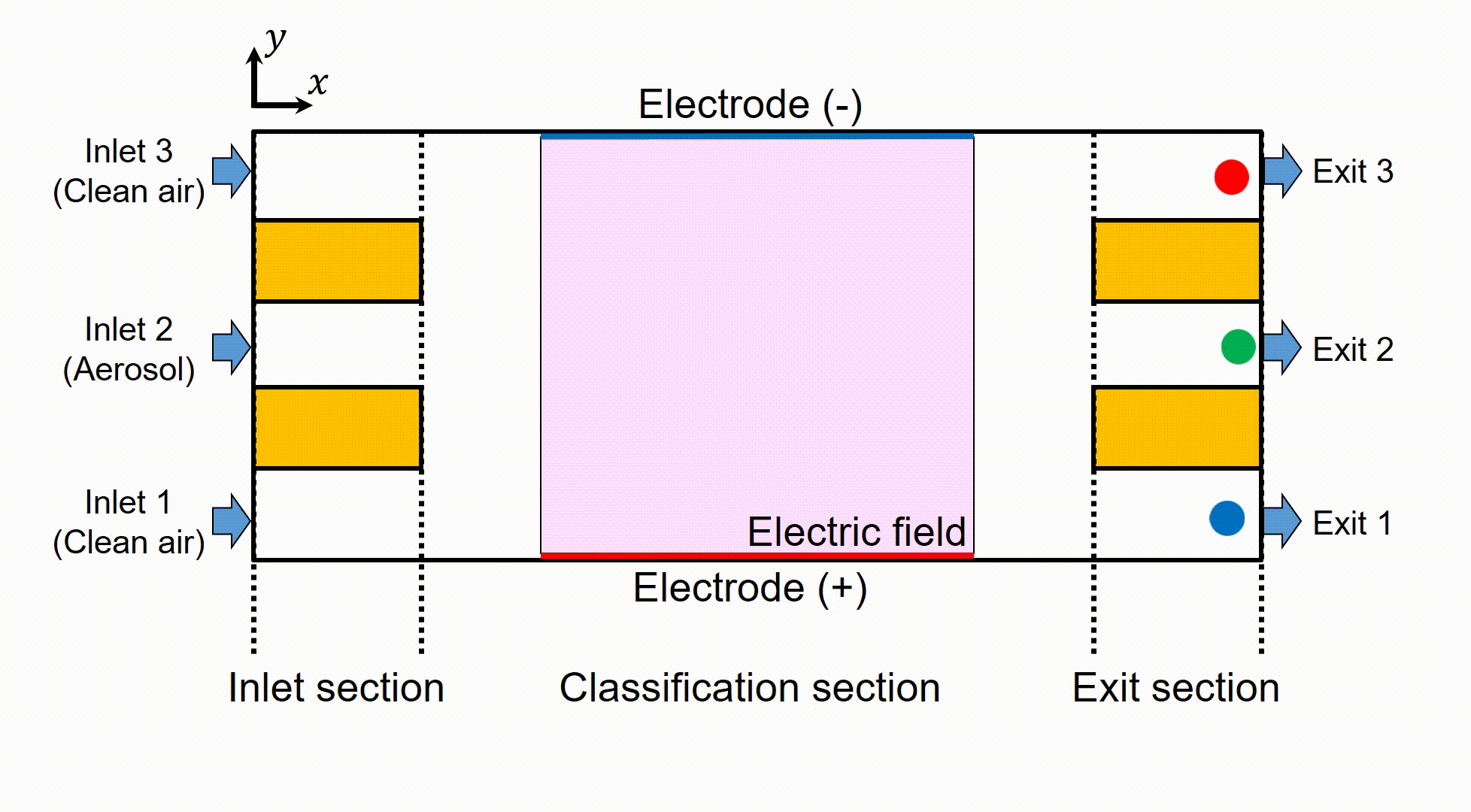
Fig. 2 Schematic of the parallel plate particle separator and classification of aerosol particles.
3. 数値解析手法
数値解析は図1に示した計算領域において,重力方向(z軸方向)を一様とみなして行った.流れ場の支配方程式は無次元化された二次元非圧縮性流れにおける連続の式とナビエ・ストークス方程式である.ここで,チャネル半幅とバルク平均速度に基づくレイノルズ数は実験と同スケールとなる7.5とした.また,電場の支配方程式はラプラス方程式である.
エアロゾル中の個々の粒子の軌跡はストークス抗力,クーロン力,ブラウン拡散を考慮した粒子運動方程式を時間積分することによって求めた.粒子のパラメータは実験に用いる標準粒子であるPSL粒子(直径0.37 μm,密度1.04 g/cm3)とした.初期条件として粒子はInlet 2から一様に流入させた.粒子運動方程式を解くうえで必要となる,計算領域内の任意の粒子の位置における流れ場,電場などの物理量は線形補間によって求めた.なお,粒子の運動が流れ場や電場に与える影響は無視して計算を行った.
4. 結果と考察
図3,4にエアロゾルの流量を実験における基準ケースと同等にした場合と,流量を基準ケースの72%に減少させた場合の粒子の軌跡を示す.なお,これらのケースにおいて電圧は印加していない.流れ場は定常かつx軸に対称であることが確認できた.また,粒子はおおむね流線に沿って移動していることが確認できた.エアロゾルの流量が実験における基準ケースと同様の場合には,粒子は中央の流路だけではなく左右の流路にも流出していることが確認できた.この左右の流路への流出は,微小なエアロゾル粒子のブラウン運動による拡散が主な原因であることがわかった.流量を減少させた場合にはエアロゾルの分布がよりデバイスの中心側にシフトし,全ての粒子が中央の流路から流出した.この理由は分級部の入口において壁面側からデバイスの中央方向への流れが誘起されており,粒子が分級部の中心に寄せられたためであるということがわかった.また,このエアロゾル流量を減少させることによる精度改善効果は実験においても確認された.加えて,中央の流路の幅を狭めることでも精度が改善されることがわかった.
実験において出口部からの粒子の流出が偏ってしまう原因の調査を行った.その結果,Inlet 2から流入するエアロゾル中の粒子の分布がy軸方向に不均一であるということが示唆された.この結果をふまえ,エアロゾル粒子の流入の偏りが改善されるようにInlet 2よりさらに上流の形状を変更した新型のデバイスを開発し,性能の検証を行っている.
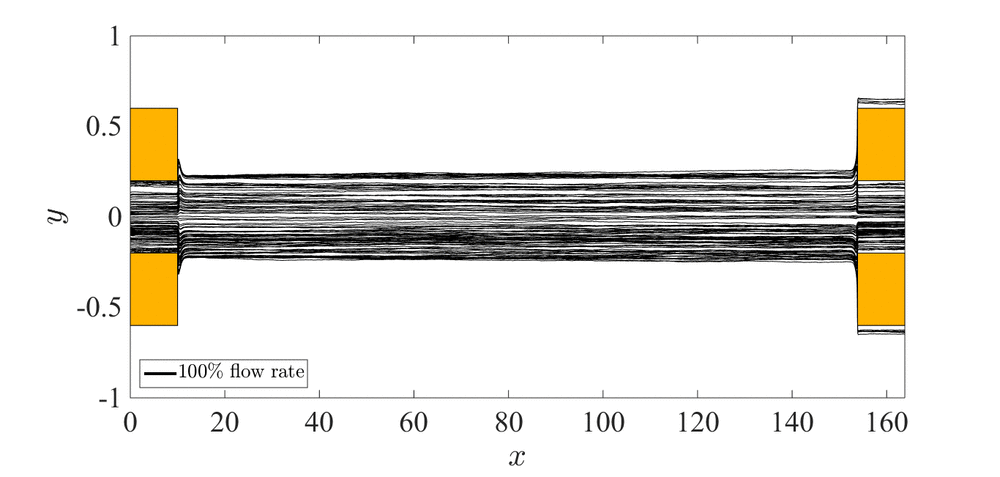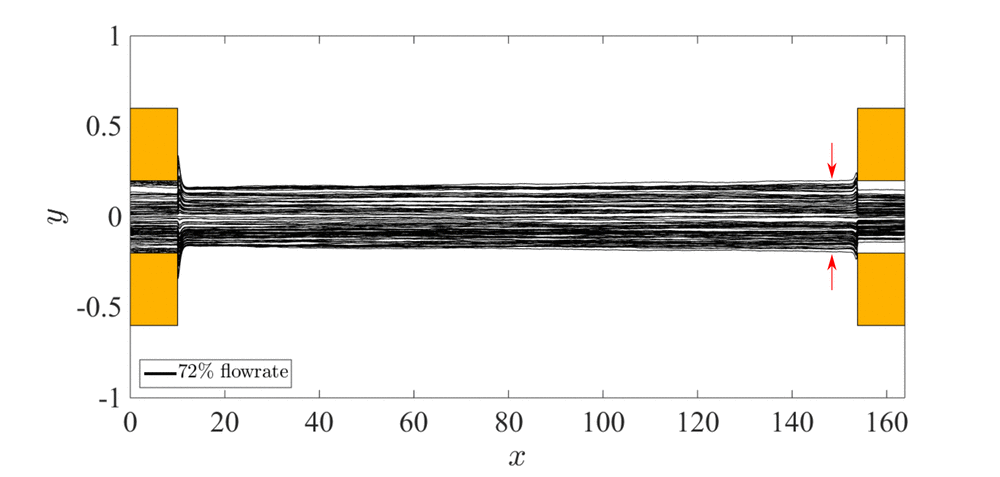
Fig. 3 Trajectories of 100 particles in the case of 100% flow rate and 72% flow rate.
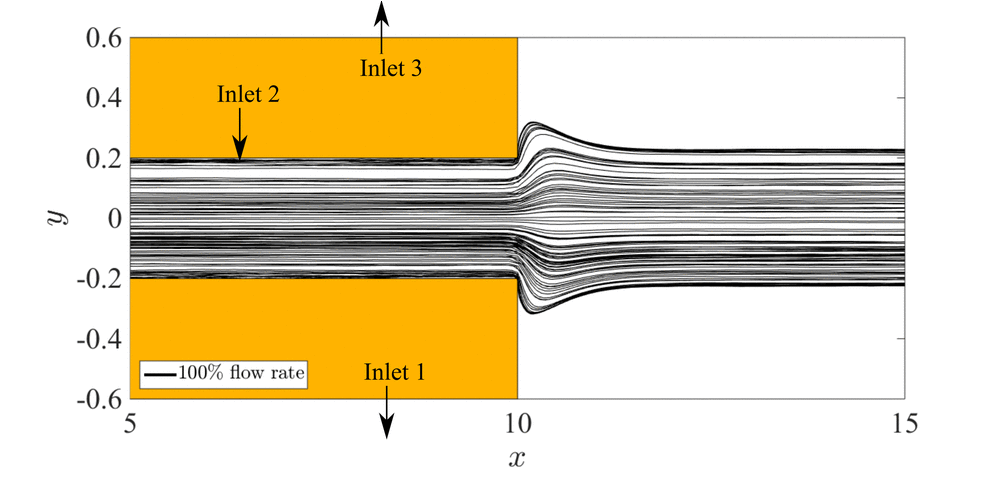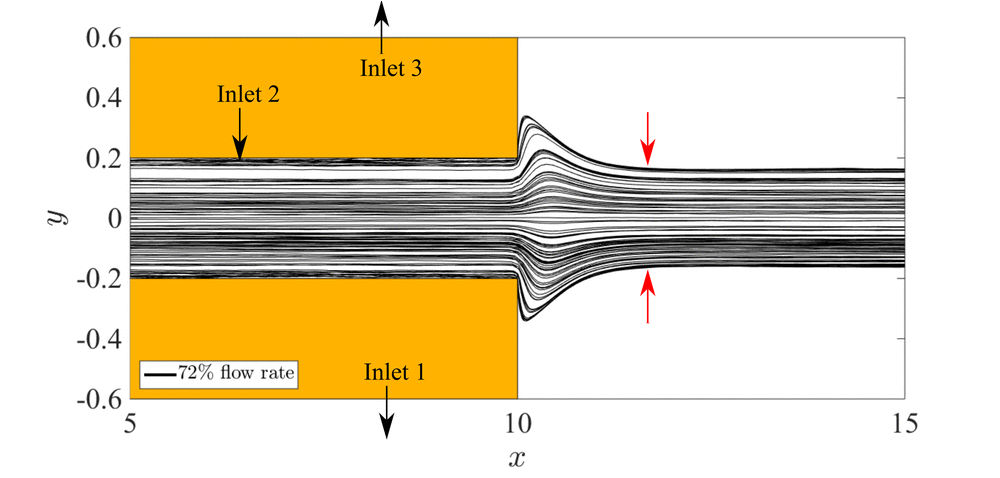
Fig. 4 Trajectories of 100 particles in the case of 100% flow rate and 72% flow rate around the inlet section.
5. おわりに
本研究では,奥田らが開発した平行平板粒子分級器の数値解析を行い,ブラウン拡散が測定精度悪化の要因であることを明らかにした.また,エアロゾル流量を減少させた場合やエアロゾルが流入する中央流路の幅を減少させた場合に精度が向上することを示した.加えて,左右の出口から流出する粒子数に偏りがある理由は,中央流路より流入するエアロゾル中の粒子の分布に偏りがあるためであるということが示唆された.
本研究の成果をもとに,今後,電場の影響に関する詳細な検討を通じて,粒子の帯電状態をより高精度に測定可能な装置の開発や,こうした装置を用いた空気中のエアロゾル粒子の帯電状態の解明を行っていく.
謝辞
本研究はJSPS科研費17H01864の助成を受けたものです.また,末筆となりますが,ご指導頂きました慶應義塾大学 小尾晋之介教授,安藤景太専任講師,ならびに当日会場にて貴重な意見を頂きました皆様に深く感謝いたします.
参考文献

