流れ　2019年2月号　目次

―　特集テーマ：JSME年次大会特集　― 巻頭言 （本澤，黒沢） バイオミメティクスで流れを掴む技術の開発 窪田 佳寛（東洋大学），望月 修（東洋大学） プラズマアクチュエータ研究会 ～5年間の活動と今後の展望～ 瀬川 武彦（産業技術総合研究所），深潟 康二（慶應義塾大学），松野 隆（鳥取大学），野々村 拓（東北大学），大西 直文（東北大学） 効率的なトライ＆エラーによる流れ制御の研究 石川 仁（東京理科大学） コアンダノズルによる遷音速、超音速不足膨張噴流のベクトル制御 社河内 敏彦（三重大学） 主流と干渉する噴流による境界層能動制御 長谷川 裕晃（宇都宮大学） 多機能OCTによる毛細血管血流速マイクロ断層可視化法 佐伯 壮一（大阪市立大学），古川 大介（大阪市立大学），伊藤 高文（東光高岳），西野 佳昭（東光高岳） 多機能OCT によるスキンメカニクス診断への応用　～皮膚抹消血管構造の可視化～ 原 祐輔（資生堂グローバルイノベーションセンター），佐伯 壮一（大阪市立大学） 　｜　リンク一覧にもどる　｜

 

効率的なトライ＆エラーによる流れ制御の研究

石川　仁 東京理科大学

1.　はじめに

　 乱流のメカニズムや渦構造に関する研究，可視化技術に関する研究を除けば，流体分野のおよそほとんどの研究は，流れを制御する目的で行われている，といえるのではないでしょうか．

　 流れの制御方法は，外部からのエネルギー授受の有無によりパッシブ方式とアクティブ方式に分類されます．パッシブ方式には形状最適化や固定デバイスによる運動量誘起など，アクティブ方式には吹き出し，吸い込み，速度や音波の撹乱を与える方法などさまざまな種類があります．また，それを実現するための制御デバイスもいろいろ考案されています．制御デバイスの分類については，本阿弥⁽¹⁾やCattafesta⁽²⁾によって詳細なレビューがなされています．例えば，吹き出しデバイスによる流れ制御を行うとすると，吹き出しの強さ，吹き出し孔の数と形状，吹き出しの与え方（連続的か，間欠的か）など，研究者は多くの制御パラメータの組み合わせの中から，それらを決定しなければなりません．数値シミュレーション（CFD）を併せて活用し，有効な制御パラメータとその値を事前に確かめることができれば非常に便利ですが，実験（EFD）によるアプローチにこだわれば，決定したパラメータを反映させた装置の製作にも費用と時間がかかります．ここでは，私のこれまでの場当たり的なトライ＆エラーによって流れ制御を試みた失敗例を恥ずかしくも紹介させて頂きながら，効果的な流れ制御の研究の進め方について考えていきたいと思います．

2.　実験計画法

　 例えば，翼のはく離制御をボルテックス・ジェネレータ（VG）でパッシブ的に行おうとすれば，制御パラメータとしてVGの数，翼前縁からの設置位置，大きさ，形状，などが考えられます．翼の迎角や流れのレイノルズ数が変われば，それらの最適値も変わるでしょう．ここで，以前より製品開発や設計の場で用いられてきた方法として実験計画法があります．実験計画法とは，効率的に精度良く要求する結果を得るために，実験を計画的に進めるやりかたを考える方法です．これをVGによる制御の研究に応用してみましょう．

　 一つめの制御パラメータをVGの数と決定して，例えば5個と10個を試すことにします．精度確保のため複数回，ここでは5回の繰り返し実験をすれば，計10回の実験が行われることになります．実験計画法では，制御パラメータの値（この場合，VGの数のこと）を「水準」といいます．ここに二つめの制御パラメータとして，VGの翼弦方向設置位置（Chord位置）を制御パラメータとして採用し，10% Chord位置と20%Chord位置を試すことにすれば，VGの数が2水準，Chord位置が2水準で，都合2x2で4回の実験が必要になります．しかし流体のようないろいろな要因が複雑に組み合わさる非線形の現象では，各実験について最低2回の実験を行わないとVGの数と設置位置の相互作用はわからないので，都合2x2x2で8回の実験が必要になります（表1）．もちろん精度確保のためにはより多くの繰り返し実験が必要でしょう．

Table. 1　VGの数とChord位置を制御パラメータとした実験．「○」が一回の実験を表す．

	VG５個	VG 10個
10%Chord位置	○○	○○
20%Chord位置	○○	○○

 

　さらに制御パラメータとしてVGの大きさを2種類，形状を2種類試そうとすると，2x2x2x2で16通りの実験をすることになります．実験計画法では，一つの制御パラメータに注目したときに，他の制御パラメータの水準が同じ数だけ含まれるように実験を選ぶことにより16通りすべての実験を行わなくとも済むようになります（表2）．これは，他の制御パラメータの一水準が同じ数だけあるので，その影響が相殺される．という考えに基づくものです．表2の場合では一つの水準が4回ずつ含まれています．多くの制御パラメータのうち，必要な結果（例えば，最小の抗力係数や最大揚力など）に大きく影響するパラメータを探索する際にはとても便利ですね．実験計画法の詳細については参考文献(3)(4)などを参照してください．

Table. 2　実験計画法による実験回数の削減．各水準が同じ数だけ含まれているので16回の実験を8回に少なくすることができる．

	VGの数	翼弦位置	大きさ	形状
実験1回目	5個	10%	5mm	三角
実験2回目	5個	10%	5mm	四角
実験3回目	5個	10%	7mm	三角
実験4回目	5個	20%	5mm	三角
実験5回目	10個	10%	5mm	三角
実験6回目	5個	10%	7mm	四角
実験7回目	5個	20%	5mm	四角
実験8回目	5個	20%	7mm	三角
実験9回目	10個	10%	5mm	四角
実験10回目	10個	10%	7mm	三角
実験11回目	10個	20%	5mm	三角
実験12回目	5個	20%	7mm	四角
実験13回目	10個	10%	7mm	四角
実験14回目	10個	20%	5mm	四角
実験15回目	10個	20%	7mm	三角
実験16回目	10個	20%	7mm	四角
	VGの数	翼弦位置	大きさ	形状
実験1回目	5個	10%	5mm	三角
実験3回目	5個	10%	7mm	三角
実験7回目	5個	20%	5mm	四角
実験12回目	5個	20%	7mm	四角
実験9回目	10個	10%	5mm	四角
実験11回目	10個	20%	5mm	三角
実験13回目	10個	10%	7mm	四角
実験15回目	10個	20%	7mm	三角

3.　はく離制御の研究の例

　 このように実験計画法は便利ですが，実際にはこのようなアプローチで流れ制御の実験をされている方はあまりいないのではないか，と想像します．

　 私の研究の例として，図1に吹き出しデバイスの一つであるプラズマアクチュエータを平板翼上に設置して，はく離の制御を試みた結果を示します．図1は平均速度 uの分布です．プラズマアクチュエータは，我々のグループが開発した，省電力型の直線型マイクロプラズマアクチュエータを採用しています⁽⁵⁾．プラズマアクチュエータは，平板翼の負圧面上で翼厚hの4倍と8倍のChord位置に設置することにしました．これは平板翼からのはく離点の位置に対して，その前（4h）か後（8h）と適当に予想して決定しました．いずれの位置にアクチュエータを設置しても制御無しの結果とほぼ同じ速度分布しか得られていません．ジェットの影響が，平板翼のはく離流れに何ら影響を与えなかった，といえましょう．もっとはく離流れの特徴である，はく離点の位置を正確に観察・測定して求め，はく離点のより近くでアクチュエータを駆動させれば良かったのかもしれません．

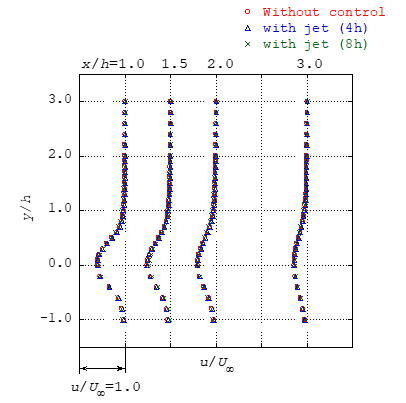
Fig.1　プラズマアクチュエータによる平板翼のはく離制御．主流方向平均速度uの分布．

4.　おわりに

　 改めて考えると，効率良く流れ制御の研究を進めるためには，まず対象とする流れ場の特徴的な構造をとらえ，それを元に制御パラメータの水準を決めることが有効だと考えます．例えば，円柱の抗力低減を縦渦の制御によって為すのであれば，はく離点がスパン方向に揺らぐ構造があることを⁽⁶⁾，境界層の摩擦抵抗低減をストリーク構造の操作によって行うのであれば，そのスパン方向間隔z⁺が約100であることを^{(7) (8)}（図2，動画），噴流の大規模渦構造の制御であれば，撹乱を導入したときにその増幅が最大となるようなプリファード周波数があることを⁽⁹⁾，などです．流れ場に内在する特徴的な構造を利用すれば，制御に必要なエネルギーも少なく済むかもしれません．

Fig.2

　 つまるところ，流れ場をしっかり観察・計測することが流れ制御の研究でも重要なのだと思います．それは乱流のメカニズムや渦構造に関する研究，可視化技術に関する研究にも共通することではないでしょうか．豊橋技術科学大学の蒔田秀治先生が，「実験装置や計測・解析方法などを工夫し，観察したい現象をできるだけ理想的な形で風洞中に実現し，そこから乱流運動の本質を純粋な形で抽出し，新しい概念の構築に資する」とおっしゃられています⁽¹⁰⁾．この言葉は流れ制御の研究を進める上でも，正鵠を射ていると思います．ここでの「新しい概念」とは，流れの制御の研究を行う我々が見つけたい効果的な制御パラメータや新しい制御方法，と言い換えることができるのではないでしょうか．

文　　　献

(1)	本阿弥眞治，“アクチュエータ空力特性の向上に基づく流れの制御技術の新たな展開”，日本機械学会論文集B編，Vol. 79, No. 808 (2013), pp. 2670-2678.
(2)	Cattafesta, L.N. and Sheplak, M., “Actuators for Active Flow Control”, Annual Review of Fluid Mechanics, Vol. 43 (2011), pp. 247-272.
(3)	鷲尾泰俊，“実験計画法入門”，日本規格協会
(4)	森田　浩，“よくわかる最新実験計画法の基本と仕組み”，秀和システム
(5)	Aono, H. et al., “Straight and curved type micro dielectric barrier discharge plasma actuators for active flow control”, Experimental Thermal and Fluid Science, Vol.88(2017)
(6)	横井嘉文，亀本喬司“二次元的な境界層はく離流れに潜在する初期の三次元渦構造（円柱上層流境界層はく離のはく離域からの可視化観測”，日本機械学会論文集B編，Vol. 57, No. 531 (1991), pp. 3273-3277.
(7)	Kline, S.J., Reynolds, W.C., Achraub, F.A. and Runstadler, P.W., “The structure of turbulent boundary layers”, Journal of Fluid Mechanis, Vol.30, part.4(1967)
(8)	Kim, H. T., Kline, S. J. and Reynolds, W. C., “The production of turbulent near a smooth wall in a turbulent boundary layer”, Journal of Fluid Mechanics, Vol.50, part.1(1971)
(9)	Ho, C.-H. and Huerre, P., “Perturbed free shear layers”, Annual Review of Fluid Mechanics, Vol. 16 (1984), pp. 365-424.
(10)	蒔田秀治，日本機械学会流体工学部門部門HP，http://www.jsme-fed.org/awards/2004/division_award/bumon.html#5