流れ　2023年3月号　目次

―　特集テーマ：流体工学部門講演会　3月号　― 巻頭言 （橋本，松田，朴） 高粘度液体吐出装置における吐出安定性 渡部 裕也（東京農工大学），釜本 恭多（東京農工大学），Jingzu Yee（東京農工大学），小林 和也(日本工業大学)，田川 義之（東京農工大学） レーザー誘起マイクロジェット生成に伴うガラス細管破壊のメカニズム解明および破壊抑制機構の開発 関口 翔斗（東京農工大学），小林 和也（日本工業大学），田川 義之（東京農工大学） 逆解法手法と数値流体力学を用いたフランシス水車ランナの最適化設計 永田 駿介（早稲田大学），李 洛中（早稲田大学），入江 達也（早稲田大学），宮川 和芳（早稲田大学） 音波照射による先端が封じられた微細孔からの気体排出 松本 悠汰（静岡大学），水嶋 祐基（静岡大学），真田 俊之（静岡大学） 　｜　リンク一覧にもどる　｜

逆解法手法と数値流体力学を用いたフランシス水車ランナの最適化設計

永田 駿介， 李 洛中， 入江 達也， 宮川 和芳 早稲田大学

１．はじめに

　3年ぶりの対面開催となった2022年11月の第100期流体工学部門講演会において，光栄にも若手優秀講演フェロー賞を頂きました．この場をお借りし，選考委員会の皆様および日本機械学会流体工学部門の皆様に御礼申し上げます．本ニュースレターでは，発表内容である，逆解法手法と数値流体力学を用いたフランシス水車ランナの最適化設計について紹介させていただきます．

２．緒言

　再生可能エネルギーの中でも水力発電は安定的な電力を供給するクリーンなエネルギーとして注目されている．特に日本国内では河川や用水路等を利用する中小水力発電の普及のため，高効率化，低コスト化の課題解決が必要である．本研究では，逆解法による設計手法と数値流体力学（CFD）を用いてフランシス水車ランナを設計し，直接法により既に最適化されたランナ（既存水車ランナ）の設計点における水力性能向上を目的とした．

３．試験装置　

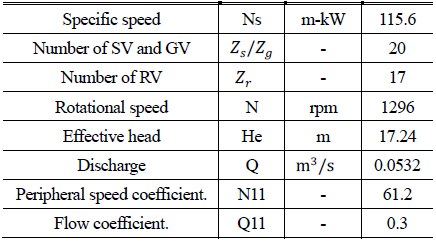
　既存水車について，性能試験を行った．図1に本研究で用いた試験装置を示す．本試験装置は，試験場屋上のオーバーフロータンクと地下の水槽を用いた静落差19.25[m]の開ループである．電気動力計により回転数を制御することで運転点を調整し，軸トルクを測定した．流量は電磁流量計を用い，有効落差は差圧変換器により算出した．代表点として最高効率点である最大流量の80[%]における仕様を表1に示す．

Fig. 1　Test appartus at Waseda University.

Table. 1　Specification of model turbine.

４．CFD解析手法・妥当性検討

　図2および表2に解析モデルと解析条件を示す．ケーシング（SC）から吸出し管（DT）の全流路，ステーベーン（SV），ガイドベーン（GV），ランナベーン（RV）は全ピッチを用いて解析を行った．回転部と静止部の境界面は全圧一定条件のもと，Mixing Planeを用いた．実験とCFDより得た性能曲線を図3に示す．CFD結果は実験結果に対し定量的に一致し，CFDが性能予想に利用可能であることを確認した．以降では本解析ソフトを利用し，ランナの最適化設計を進める．

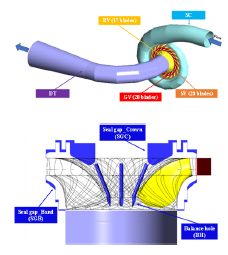
Fig. 2 Computational domain.

Table. 2　Computational condition.

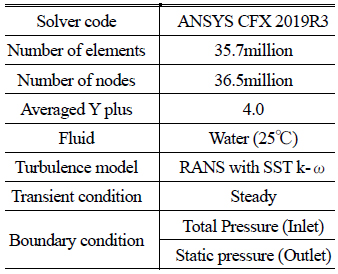
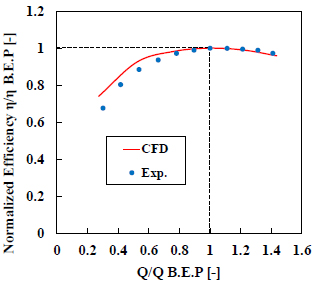
Fig.3 Turbine performance.

５．逆解法理論

　本研究では，Zangeneh⁽¹⁾により商用化された3次元逆解法理論を利用する市販逆解法設計ソフトTURBOdesign（ADT社）を用いた．非圧縮ポテンシャル流れにおいて，翼面の静圧差である翼面負荷⁽²⁾は，

(1)

で与えられる．ここで，は翼面子午面速度，mは子午面距離，は角運動量である．本式を利用し，入力パラメータ①子午面形状，②羽根負荷分布（図4），③回転数，④羽根厚分布，⑤羽根枚数，⑥スタッキング条件（図5），⑦入口仕様を用いて羽根形状に関する逆問題を解く．

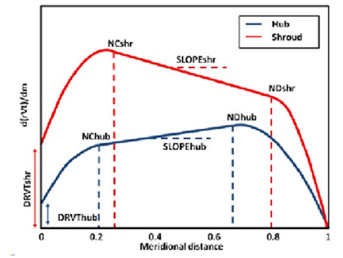
Fig.4 Streamwise blade loading ⁽²⁾.

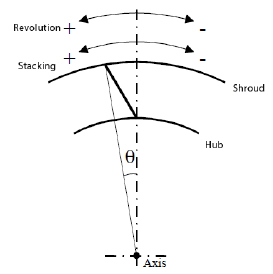
Fig.5 Stacking condition ⁽²⁾.

６．ランナの最適化設計

　図6に示すようなフローにて設計点におけるランナの最適化設計を行った．まず，CFDと実験計画法により①子午面形状を決定後，②ランナ角運動量を決定した．②翼負荷分布と⑥スタッキング条件は，ADT社汎用ソフトであるTURBOdesign Optima (TD-Optima)内の遺伝的アルゴリズム（GA）を用いた最適化により検討した．その後設計した翼形状に対しCFDで性能評価，内部流れの分析を行った．要求性能を満たさない場合には翼負荷分布とスタッキング条件を再検討する．本研究では設計フロー前半で決定した子午面形状や角運動量は変更せず，③回転数，④羽根厚分布，⑤羽根枚数は既存水車ランナと同じ値を利用した．

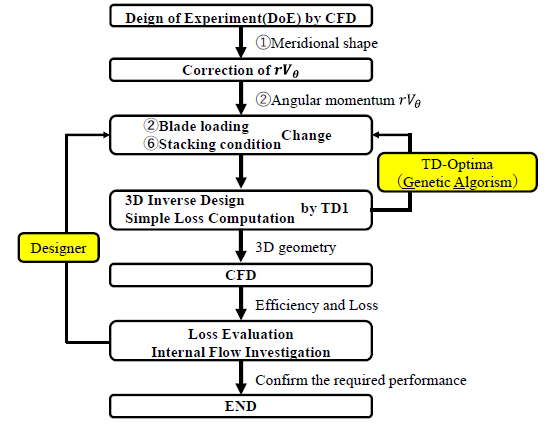
Fig.6 Design flow.

6.1 CFDによる実験計画法を用いた子午面形状の決定

　入力パラメータの①子午面形状について，CFDとL18直行表の実験計画法を用いて検討を行った．今回は，寸法の制約より，子午面形状パラメータの中でもランナ出口形状に関わるものや，クラウン形状に関わるものを因子として選択した．水準は，筆者研究室にて所有するデータベースより決定した．解析モデルには翼列1ピッチのGVとRV， DTを利用し，設計点でのRVとDT損失の合計が最小となるような水準を選択した．図7，8に得られた要因効果図と子午面形状を示す．

Table. 3 Runner parameter in DoE.

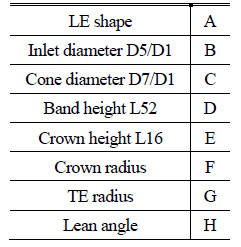
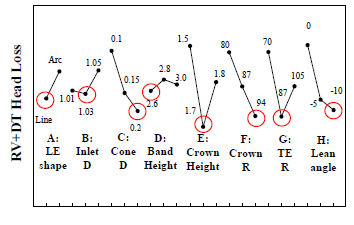
Fig.7 Sensitivity analysis results.

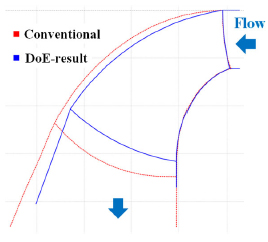
Fig.8 Meridional shape.

6.2 ランナ角運動量の補正

　入力パラメータの②羽根負荷分布の一つであるランナ角運動量について検討を行った．ランナ入口は，上流に存在するSC，SV，GVによって決定され，それら壁面境界層の影響により，壁面近傍と主流域では異なる分布を持つ⁽³⁾．そこで設計仕様のオイラーヘッドより一次元的に算出した値を従来水車のデータにより補正することで，実際の流れに近い入力値を与えた（図9）．ランナ出口は，設計点で0となるように設計されることが一般的であるため，高さ方向一定に無旋回を入力値とした．本補正によって翼負荷量は設計値より0.62[%]増加したが，設計仕様への影響は小さいとした．

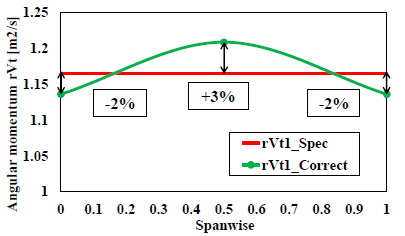
Fig.9 Correction of spanwise at RV LE.

6.3 ランナ負荷分布の検討

　ランナ翼負荷分布および⑥スタッキング条件について，GAを用いた最適化手法にて検討を行った．設計パラメータには図4，5に示すパラメータのうち合計13個を選択した．目的関数はランナ損失を意味するTD-Optima内の損失係数とし，最小となるよう最適化を進めた。本研究では各世代の個体数を50，世代数を50として計算を行っている．図10にGAの最適化履歴を示す．計算が進むにつれ損失が低下している様子が確認できる．その中でも，ランナ損失が大きいもの（RV-A）と小さいもの（RV-B）についてCFDを行い，負荷分布およびスタッキング条件がランナ内部流れに与える影響を分析した．

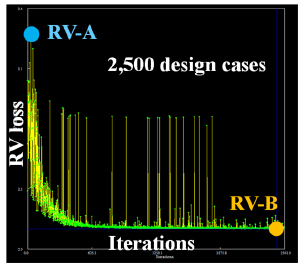
Fig.10 Convergence history of the RV optimization by Genetic Algorithm.

　ランナ内の流れには，回転による遠心力，コリオリ力，流路曲率による遠心力等が働くため複雑な二次流れを形成し，それらの衝突，混合により損失が発生する⁽³⁾．つまり，ランナ内で発達する二次流れを抑制することが，ランナ内損失の低減に繋がる．Zangenehら⁽⁴⁾は下記の二次流れに関する流れ方向方程式と相対系運動量式を導出し，二次流れは(reduced pressure)の勾配により評価可能であるとしている．

	(2)
	(3)

　図11に、RV-AおよびRV-Bの翼面の無次元分布（）と負圧面近傍の速度ベクトルを示す．損失の大きいRV-Aではランナ入口付近での高さ方向圧力勾配が大きいために，負圧面でクラウン側からバンド側に流れる強い二次流れが生じている．一方，圧力勾配が小さいRV-Bでは入口付近での二次流れが小さい．つまり，ランナ入口付近の高さ方向圧力勾配を抑制することがランナ内二次流れの抑制に効果的であることが分かった．RV-Bのような，クラウン側が前方負荷，バンド側が後方負荷，入口バンド側が回転方向に先行するようなスタッキングを与えることで，ランナ入口負圧面における高さ方向圧力勾配が減少し，ランナ損失を低減できる．

(4)

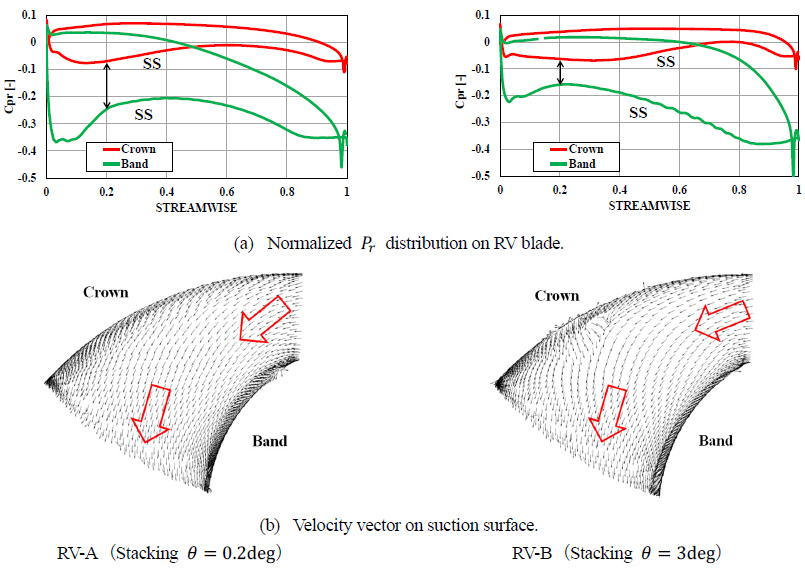
Fig.11 Comparison of RVs’ internal flow (CFD).

6.4 CFDによる性能予想

　前述の考察をもとに負荷分布とスタッキング条件を再度検討し，設計した最終形状（Newランナ）を取得した．SCからDTを含めたCFDにより性能を予想し，得られた設計点における各部損失割合を図13に示す．各損失ヘッドの式より，既存水車損失の合計を1として算出した．ただし，はランナ内流量である．逆解法を用いたランナにより既存水車損失の約4[%]が低減されたことを確認した．

	(5)
	(6)
	(7)

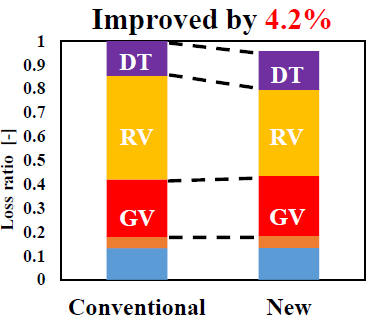
Fig.13 Loss ratio (CFD).

７．結語

　本研究では，逆解法とCFDを用いて，直接法にて最適化されたフランシス水車ランナの設計点での水力性能向上を目的とした最適化設計手法の構築を行った．子午面形状やGAを用いた翼負荷分布，スタッキング条件の検討から，従来水車損失の約4[%]を低減した．本設計手法により，CFD解析の実施数が大幅に減少し，短時間かつ低コストでフランシス水車ランナの最適化設計が可能であることを確認した．

謝辞

　本研究はWISE（早稲田理工学術院総合研究所）のプロジェクト研究「水力ターボ機械システムの高性能化，高信頼性化研究」の一環として実施した．

文献

(1)	Zangeneh, M., “A Compressible Three Dimensional Blade Design Method for Radial and Mixed Flow Turbomachinery Blades”, Int. J.Numerical Methods in Fluids, Vol.13 (1991), pp.599-624.
(2)	Help, TURBOdesign Suite 2022.1.
(3)	宮川和芳，小室隆信，“水車・ポンプ水車の内部流れと高性能化技術”，三菱重工技報，Vol.35(1998)，pp.166-169．
(4)	Zangeneh, M., Goto, A., and Harada, H., “On the Design Criteria for Suppression of Secondary Flows in Centrifugal and Mixed Flow Impellers”, ASME, J. Turbomach, Vol. 120(1998), pp. 723–735.