流れ 2011年4月号 目次
― 特集テーマ: 流れの夢コンテストの10年 ―
| リンク一覧にもどる | |
アイデア一本を何十倍にも面白く見せる方法
村井祐一 |
1.答え
未完成の魅力,それが大事なのである.仕上げをしてしまっては駄目なのである.仕上げには幾つかのアイデアがあるが,そのうち一つを選んで製作してしまったとき,作品の魅力の大半が消失すると言ってよい.作品の仕上げ方に,討論の余地を残して終えるのがいい.思えば技術というものは,磨いて磨いて,その繰り返しで完成の域に近づく.磨いている最中が人を惹きつける.技術者は,完成に到達する道の中にいるとき,最高の興奮を感じ,努力を惜しまない.こだわりある職人は,簡単な加工を依頼しても,面倒くさいと言って跳ね返す.これは難しいと思うが出来るでしょうかと無理をお願いされたとき,いま忙しいからとは言わなくなる.創意工夫の力が試されているとイキに感じ,バカにするんじゃないと言って優先して取り組んでくれる.それが技術と人間のかかわりだ.世界中の技術畑で,そういう歴史が刻まれてきた.
2.魅力
流れの夢コンテスト,それは上述のような価値観を浸透させてくれている.それゆえ,当研究室の出展作品が過去6度の入賞歴をもつことになった.つまり,大掛かりで高度な技術を投じた大作を超えて,手作りの未熟な作品が上位の賞を受ける.視聴率が復活した紅白歌合戦で,大かがりな舞台設備で熱唱するのと,無地のカーテン一つをバックにして素朴に歌う歌手を見る.歌の魅力が伝わるのはどちらか問うまでもない.夢コンも,そのつもりで学生にし向けて出展してきた.流体の面白さを伝えるのは素朴さだ.素朴な場合に限って,そこにはリアリティ(具現化)とアイデア(空想)が共存できるからだ.作品を見た人が,未熟な作品をみて「自分ならここからこうするね」とアイデアを上乗せしてくれる.会話がはずむ.
コンテスト会場で説明する学生と審査員のやりとり,それが全てだ.一つの作品に幾重もの意味を閉じこめる方法をとった場合は,審査員が,なるほどなるほどと首を縦に振る.では一つの作品が一つの意味しかないが,そこからの展開を説明した場合はどうだろうか.審査員は作品を創る立場の心理に誘導される.造形や焼き物の品評も似て非なるところがある.作品に込められた意味を作者が全て明かしてしまっては幻滅だ.そこに込められた主張をくみ取ろうとするとき,そこから想像される世界の広さと深さで真価が決まる.見る人の志が高いほど,作者に対する評価も大きく振れよう.些細な工夫を読み取って,時に,高い評点を与えてくれる場合もある.著者はたまたま文学の流体力学的な可視化も研究している(1).そこでも同じ議論がある.文学作品は十人十色の解釈と批評をもつ.だからこそ価値がある.科学論文は百人いても唯一の解釈しか存在しないように書く.それゆえ科学論文の書き方というものがある.法律の言葉はまた別だ.その論理的な厳密さは,恣意的に複数の解釈を共存させるために使われている.流コンの作品の品評基準は,これらのうちどれに対応するだろうか.魅力という観点ならば,ゆるぎなく文学の批評に近い.人が創って人に伝える.その媒体となるものは,文学では言語,夢コンでは流体ということだ.
3.作品
どうぞ感動をお楽しみ下さいとナレーションが入ると失敗しやすいものだ.なんだこの作品では無理だな,という第一印象で始まるのが良い.にらめっこの原理を知っているだろうか.最初に全力で変な顔をしてはいけない.地味な動きから入るほうが勝つ.当研究室の学生達が出展した作品は,そういうものばかりである.
3-1. 第2回最優秀賞作品「アドベンチャーバブル」(2002年)
研究室に在籍する韓国人留学生のパク君が出展した(当時,著者は福井大学に所属).会場は名古屋の日韓流体工学会議2002である.Fig. 1のようにアクリルで10センチ角の迷路を造っただけだ.ただし水を封入して一つの気泡を入れる.少し水漏れする点が,エレガントなコンテスト会場に”水”を差す痛々しい作品だ.しかし彼の説明とそれに対する評価はうなぎ登りだった.固体粒子を運ぶときとは操作が異なる.それはそうだ,駆動力が浮力だから盤面の傾斜を逆にしなければならない.ただし実際にタイムを競ってみると,もっと奥が深い.急ぐほど気泡は勝手気ままな進路に向かう.それを体験した気泡運動に詳しい人が,その原因を我先にと教えてくれる仕組みだ.実体として運動しているのは気泡のすぐ周囲の液体である.盤面の加速は,気泡に大きな付加慣性力を与え,過剰加速を生む.回転させると揚力と圧力勾配によりあさっての方向に曲がる.その動きは,格好良く言えばあたかも反重力のように,格好悪く言えば,大人をバカにする悪ガキのような振る舞いだ.今では bubble mazeという名前で携帯ゲームソフトにも登場している.これを真似たかは知らないが,誰でも思いつくゲームである.ただしその力学は難しい.
スタートからゴールまでの正解ルートの距離は85cmしかない.抗力と浮力の平衡だけを考えた理論上のベストタイムは5.0秒だ.しかし17名の競技者の統計では平均で92.0秒かかった.空気中の粒子の迷路の場合と比較して3倍となった.特にその分散が大きいのが気泡の特徴だ.壁面との衝突では応答に分散があるのも不可制御要因になっている(2).会場を笑わせたのは裏統計データだ.研究室全員のうち気泡の研究をしている学生は丁度半分であった.気泡チームと非気泡チームでの平均タイムを調査したところ,それに有意な差が確認されなかった.気泡の基本的な運動も制御できないのに,乱流場の気泡の運動の特徴を研究する資格などない,と,10cm角は教えてくれた.後日,福井新聞にこの最優秀賞作品が,詳しい原理説明付きで紹介された.
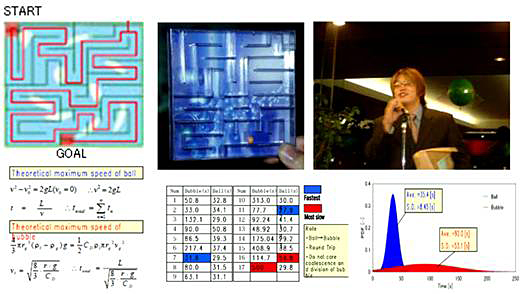
Fig. 1 気泡の迷路「アドベンチャーバブル」と作者パク君によるその理論および実験データ
3-2. 第7回一樹賞作品「デスクトップトルネード」(2007年)
アメリカでのバックパッカー経験のあるM1の吉本君の作品で,竜巻の国から持ち込んだテーマだ.当時,彼の修士論文に向けた研究は,竜巻が重い粒子や液滴を内部に捕獲すると,不安定になるどころか,かえって中心圧力が低下して強固な竜巻になる(3)ということを実験で証明することであった.このために高さ2mの混相人工竜巻発生装置の製作に新車一台分のお金をかけた.その設計・製図・製作に1年以上をかけてしまった.その間に,夢コンの機会を利用して2週間程度でミニ竜巻を作ることになった.製作したのは,よく知られている人工竜巻の原理を流用したもので,直径10cmのアクリル円筒がメインボディである.それが何故,最高賞に輝いたのか.
彼は予旋回を与える流入口と可視化剤の注入方法で試行錯誤を繰り返した.そこには実験流体力学のエッセンスがある.他方,竜巻を観ていると流体を研究していることの誇りを感じさせてくれる.高速にスピンしてダンスする手のひらサイズの竜巻は飽きない.それを卓上で自由自在に発光させて制御できれば商品化の道も開ける.キャッチフレーズは「竜巻をミニチュアサイズでカスタマイズ」.製作した作品はFig. 2の左の写真である.外観をみても迫力があるわけでない.しかし竜巻を発生させカラフルな光を入射すると,直径10mmの渦核をもつ虹色の竜巻が生まれる.左右の目で見ると竜巻の三次元構造が把握できて,その流体力学的な美しさに時間を忘れる.紅茶でも入れて,眺めていたい.となれば,紅茶を入れるポットのようにしてみれば?それが勝手に考えた市場投入型デザインで右側の図のとおりである.デスクトップトルネードはポットになって世界の家庭に入り込む.家族で流体力学の時間ができる.「手を入れて竜巻を切ることができるの?」「竜巻の直径はどこまで小さくできるの?」「出口が二つあったらYの字に分かれると思う?(4)」思えば香水をつくる流路から多数の流体力学法則が発見された.慌ただしい日常から抜け出して,紅茶を飲みながら流体力学を語りませんか?
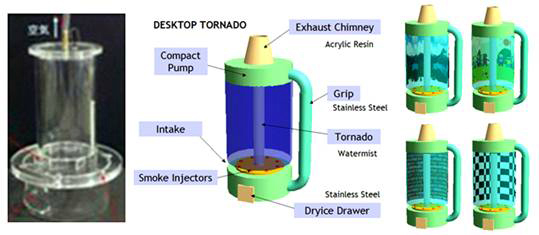
Fig. 2 湯沸かしポット型竜巻「デスクトップトルネード」とインテリア市場投入デザイン

Fig. 3 夢コンでの一樹賞受賞を放映するUHB北海道放送夕方ニュース
3-3. 第8回最優秀賞作品「バッティングあわー」(2008年)
研究室の最重要ランクに位置づけられているイベント,機械知能工学科の研究室対抗ソフトボール大会にちなんだ作品である.四年生の南部君が野球盤を製作した.ただしボールは気泡である.2002年作品のアドベンチャーバブルは気泡の性格を熟知していても,制御するのが難しかった.今回はピッチャーが投げるアワを回転するバットで跳ね返すだけである.ピンボール盤のように盤面を傾斜させて,単一気泡を浮力によってバッターボックスに向かわせる.癖のないど真ん中の直球を打つだけだ.しかしこれが打てない!金属バットを振ると,一塁側のファールにしかならない.振り遅れるわけがない.球速は20 mm/sの超スローボールである.どうやら気泡を打つための全く別の打撃理論が存在するようだ.その理論が完成せぬうちに,展示の日を迎えた.
当日は気泡に詳しい先生達,野球盤を懐かしむ人たちで囲まれた.気泡力学の重鎮も一塁側ファウルしか打てなかった.あまりファウルで粘られても困るのでファウゾーンはアウトとした.ファウルは振り遅れの認識をもたせるので,早いタイミングでバットを振るようになる.しかしそれは事態を悪化させる.会場での体験者の意見と液相の可視化結果を集約すれば,正しい気泡打撃理論はこうである.つまりバットの回転でバット軸方向に圧力勾配をつくる.それにより気泡をバットのグリップ付近に誘導する.その後,バットをしっかり最後まで振り切る.それによって振り切り終わった瞬間に渦が出来る.この渦はいつもライト側に移流する.気泡が渦核に入り込んでいれば渦は安定してヒットゾーンまで飛んでいく.要するに一言にすれば,最後は液相の渦度で打つのである.ちなみに図のグラフにあるとおり,著者の30回のフリーバッティングの長打率は4割3分3厘で,学生達に完敗してしまった.そのかわり第28球目の記録にあるとおり,私だけが本塁打を飛ばしている.私は気泡の研究者であることが証明された.
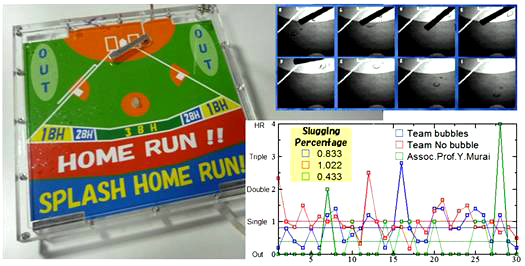
Fig. 4 気泡をバットで打つ野球板「バッティングあわ~」とその打撃理論および長打率比較
3-4 第9回優秀賞作品「ザ・サードディメンジョン」(2009年)
粘弾性流体の計測を卒論テーマにすることとなった四年生の白鳥君による出展である.立体テレビを,流体を発光体として製作するというものだ.3D映画だの飛び出るテレビだの3DSだのと,活発な商戦が展開しているが,流体屋ができること,それは流体をボクセルとした三次元映像装置だ.原理にはCTを用いる.しかし普通のCT(5)と入出力関係が逆だ.立体空間に浮かび上がらせたい形を多方向の投影像に分解する.あとはそれを重ねて投影して,実空間で立体像に戻す.CTとはコンピュータで断層を復元する装置を意味するが,この場合は光が断層を復元する.何も計算する要素はないので,光の速度でCT解析をしていると言っても大袈裟ではない.
作品は実に素朴だ.Fig. 5にあるように百円ショップミラーを12枚,あとは液晶スクリーンプロジェクタとパソコンである.ミラーを放物配置して液体中に結像させる.12方向からの逆投影だと,右側のサンプルのような立体像を描くことができる.垂直方向に変化させれば,三次元像となる.実演はしていないが,動画を使えば動く立体像も映し出すことができる.この素朴なアイデアで地味な活躍をしているのが粘弾性流体だ.液体内で光を丁度よく散乱させるために白色の粒子を分散させる.長時間の照明で発熱して対流が起こると,立体画素が不均一となり,しまいには沈降または浮上分離してテレビが真っ暗になる.単に高粘度にするたけでは解決しない.粘弾性流体は粒子を正確に静止させる機能がある.製作費がとても安いので,あとは解像度だけの問題である.ハードルは低い.高品質のミラーを使って,その数を50ぐらいにすれば,一人の人間の細かい形状と色,動きまで再現できるはずだ.粘弾性流体による3Dテレビが家庭向け大量生産に入るとき,実験流体力学は思わぬ特需を迎え,多忙を極めるだろう.
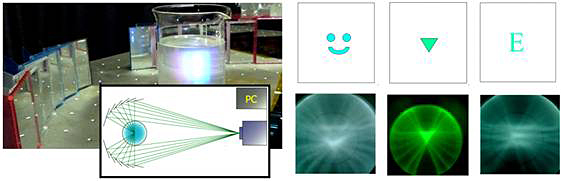
Fig. 5 粘弾性流体の中で立体像を作る「ザ・サードディメンジョン」とそのサンプル画像
3-5 第6回特別賞作品「テイラークエットマグカップ」(2006年)
機械学会の主催で2005年に札幌で第14回テイラークエット国際会議が開催された.30年の歴史をもつこの国際会議はテイラークエット流れの魅力のとりことなった欧米の非線形流体力学者のファミリーで構成されている.M1で変調波動渦の発生の実体(6)を探る野村君が,夢コンで出展したのは,片手で持てるテイラークエット可視化装置で,中に飲み物を入れることができるものだ.作品はFig. 6左の写真とおり,機械屋が考えるデザインのままだ.しかし流体屋が楽しむとき,香り立つコーヒーは,学問の深みを感じさせてくれる一品となろう.野村君によれば展示会場において,持ち帰りたいぐらいだと賛辞を多数頂いたそうである.回転速度によってクエット,テイラー渦,波動渦,変調渦,乱流渦の5つのモードを楽しむことができる.テイラークエット流れの専門家達は,さらに詳しく細分化されたモードが見えるという.ただし熱いコーヒーを入れるので,内円筒入熱が伴って共存対流になると心配する.ならば,感温液晶を入れて温度も可視化して,ついでにリングライトを上下に入れて照明し,などなど,多数,仕上げに向けたアイデアを提供して頂いた.
3-6 第8回優秀賞作品「流体力学的札幌市」(2008年)
当研究室は1972年の札幌冬季オリンピックに向けて建設された1969年製の風洞がある.いまでもスキージャンプやスノーフェンスなどの北海道らしい流体工学実験を担っている.そんななか,札幌市中心部の気流構造を再現する風洞ビルモデルが製作された.M1の繁富君はこれに数値計算結果を投影するという,目的外使用の面白さで夢コンにエントリーした.EFD-CFDハイブリッドだとか,数値風洞だとか,関連キーワードを思い出すが,それほど論理的なものではない.ただ,それを見せることで,何を感じるかを問うのである.Fig. 6の右図は,模型の上部からプロジェクタによりビル周りの流れの数値計算結果を投影した.その立体感は,数値計算結果を手づかみできるような現実感を与えるものになった.航空写真を投影すれば,実物そのものに見え,レストラン情報付の地図を投影すれば,立体ガイドになる.そして緑化計画の地図として,季節の木々・花々を投影したり,車や歩行者も動画で投影すれば,札幌市長になったかのようだ.ビル周りの渦度や乱流エネルギー分布をカラフルに投影したり,動くトレーサー粒子を投影する.揺らめいて流れるビルのすき間の風は,両目で見ると現実そのものだ.流体力学による札幌のイルミネーションである.

Fig. 6 「テイラークエットマグカップ」と3次元VRアート「流体力学的札幌市」
4.結言
このニュースレター号で,私は,他の方と対極的な記事を書いたことになったかも知れない.完全なるものを目指せとか,どうせ創るなら立派なモノを志せと書かなかったためである.むしろモノヅクリは途中で切り上げたほうが良いとまで書いた.工学の学生向けとしては非教育的である.しかし,完成という結末そのものには殆ど意味がない.そう言い切ることにしよう.妙に素朴で中途半端な作品ばかりが数々の受賞を頂いてしまったことに対する正当防衛かも知れない.しかし,何度も繰り返したように,結末に向かって努力している道の丁度真ん中でコンテストを迎える.それで良く,むしろそれがベストなのである.出展した学生が作品の工夫をどう実現していくかを一番強く考えている瞬間である.人と技術が一体となっている瞬間の輝きを見せる.
5.謝辞
研究室の学生達のコンテストに向けた努力を,技術面と教育面で指導して下さっている当研究室の山保技術員と田坂准教授に深く謝意を示します.
参考文献


