流れ　2013年10月号　目次

―　特集テーマ：2013年度年次大会　― 巻頭言 （杵淵，玉野，真田） 「流れのふしぎ科学教室」－楽しい流れの実験教室と教員・科学ボランティアのための研修会に参加して－ 田原功一郎（米子工業高等専門学校） 竜巻の発生環境を再現する試み 佐々浩司（高知大学） 水泳動作を行うロボットに作用する非定常流体力の計測とモデル化 中島求（東京工業大学） EFDワークショップ 流体力とせん応力の計測 亀田孝嗣（近畿大学） 　｜　リンク一覧にもどる　｜

 

EFDワークショップ　流体力とせん応力の計測

亀田 孝嗣 近畿大学 工学部

1.　はじめに

　 2013年度年次大会のワークショップにて，北海道工業大学　平元理峰先生ら他4名による企画「流体力とせん断応力の測定」で講演させて頂きました．その講演のすべてではありませんが，ここでは山口大学理工学研究科の望月信介先生および退職された大坂英雄先生と共同で研究を行ってきた壁面せん断応力の測定に限定して紹介をさせて頂きます．

　 流体工学上，物体表面上に形成される乱流境界層は物体に作用する抗力や流れのはく離現象と関連して重要な流れの一つである．これらの予測には，基礎的研究として平均速度場や乱流場の相似則(代表例として壁法則)の検証が重要な役割をなす．これら相似則の検証には，代表尺度の一つである摩擦速度の信頼ある評価が望まれる．ここで，摩擦速度u_τは壁面せん断応力τ_wと流体の密度ρを用いて，
　　　　　　　　　　　　　　　　　u_τ ≡ (τ_w/ρ)^1/2　　　　　　　　　(1)
と定義される．τ_wの評価法には，一般的に壁法則法，運動量法および直接法の3つの方法が知られている．壁法則法は，クラウザー線図法，プレストン管法やサブレイヤーフェンス法などがある．最近の研究では，壁法則中の定数(カルマン定数)が流れ場の種類(外力，境界条件の違い)やレイノルズ数に依存して変化することが報告⁽¹⁾されており，その使用には注意が必要である．これらの方法により求められたu_τは壁法則の成立を前提としており，壁法則の成立可否の判断には使用できない．運動量法は，運動量積分式や力の釣合いによりτ_wを評価する方法である．これらの方法では，運動量厚さや壁面静圧の流れ方向微分操作が必要なため流れ方向計測間隔や近似関数の検討が必要である．直接法は，壁面の一部から切り離した微小な面積要素に作用する流体力を計測する方法である．この方法の利点は，壁法則などの相似則を利用しないことや流れ場の性質(圧力勾配や壁面粗さ)によらないことが挙げられる．一方，欠点としては，計測装置の構造が他の二つの方法に比べ複雑になること，微小な力の計測が必要であることや壁面の一部から切り離したことで二次的な力が付加されることである．

　 今回，低乱流境界層風洞にて行ってきた乱流境界層の壁面せん断応力の計測について，力計測装置の原理とその測定例について簡単ではありますがご紹介致します．

 

2.　直接測定装置の原理と各種寸法

　 壁面せん断応力直接測定装置は，望月信介教授および大坂英雄 前教授が設計・製作した装置⁽²⁾をベースにして製作されたものである．図1にその概略図(断面図)を示す．図1の装置は，粗さ要素高さkが流れ方向距離に比例して増加する二次元矩形粗面に作用する壁面せん断応力を計測するために製作⁽³⁾されたものである．壁面せん断応力は，浮動片要素に作用する壁面せん断力を浮動片要素面積で除すことで評価できる．浮動片要素 は，二枚のリン青銅板バネ (厚さ0.2 mm，幅15 mm) によってパラレルリンク式機構で支持されている．浮動片要素の平面形状は加工のし易さおよび精度を考慮して円形となっている．図2には，直接測定において重要な装置幾何寸法を示す．浮動片要素と周囲板の隙間寸法 (ギャップ寸法)Gは，ギャップが粗さとして流れ場に影響を与えないように実験を通じてGu_τ/ν < 10 ⁽⁴⁾となるG = 100 µmとする．周囲板と浮動片要素の高さの差であるミスアラインメント寸法hは，それ自身による流れの衝突やはく離の影響を小さくするために浮動片要素周囲に配置した3個のマイクロメータによりh = -10 µm ～ 0 µmの範囲に収まるように調整 ⁽⁵⁾ される．また，直接測定装置内圧力P_cと乱流境界層内圧力(代表的に壁面静圧)P_sの差ΔPは，ギャップでの流体の運動量交換に寄与し，二次的な力の発生要因となる．これに関して山口大学理工学研究科修士論文でΔP/τ_w = O(1)でD⁺ (粘性長さν/u_τに対する浮動片要素直径Dの比) ≥ 1000のとき，浮動片要素に作用する全流体力F_T (壁面せん断力と二次的な力の和)に対するギャップによる生じる二次的な力Fsの比F_s/F_Tは数%程度となることが示されている⁽⁶⁾．なお，ΔP/τ_w = O(1)は無次元圧力係数C_P (= DP/(1/2 ρU₁²)，U₁は主流速度)で表すと，C_P = O(c_f)，c_fは局所壁面摩擦抵抗係数，となる．ここで，滑面乱流境界層を例にΔPやDの値を見積もってみる．運動量厚さθに基づくレイノルズ数R_θ = 5000とすると，Kármán-Schoenherrの式からc_f = 0.00300となる．U₁ = 10.0(m/s)とすれば，C_P = O(0.1%)でD ≥ 40(mm)となる．図1の装置では，流れ方向距離x = 1570，2180および2800mmの3箇所で粗さ要素が5ピッチ分の平均的な流体力を計測することを考慮して，浮動片要素直径Dはそれぞれ59.1，77.4および89.5mmの寸法が採用されている．上記の幾何寸法の注意事項に加え，図1の本装置には浮動片要素に流体力が作用して生じるギャップの不均一性の影響を小さくするために，ゼロ変位機構を設けられている．その機構は，浮動片要素支持脚に設けられた永久磁石(サマリウムコバルト：磁束密度3200G，3φ×9)と自作電磁コイル(被膜線直径0.2 mm，巻き数100)からなる．その方法として，まず浮動片要素支持脚に備え付けられた対象平板位置を静電容量式変位計(岩通テクノシステム社製，分解能0.001 µm)により計測し，つぎに変位計の出力値の平均値(平均化時間40 s)がゼロとなるまで電流値を増加させて電磁コイルにより反力を発生させる．図3に浮動片要素に作用する接線力(摩擦力)と自作電磁コイルの電流に関する静的較正曲線の結果を示す．較正曲線は極めて良い直線性を示す．

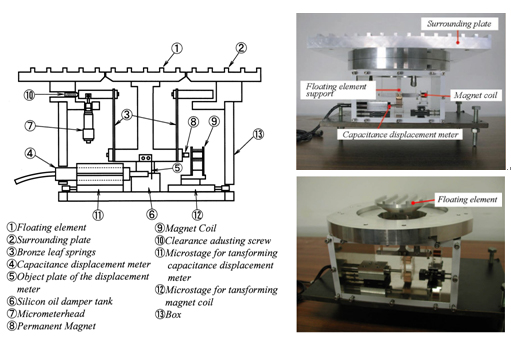
Fig. 1  Direct measurement device with a floating element

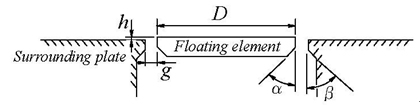
Fig. 2  Geometry of direct measurement device

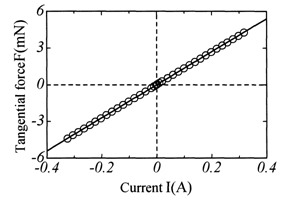
Fig. 3  Calibration carve between tangential force acting on the floating element
and current applied to magnet coil

 

3.　壁面せん断応力の計測例

　図4に図1の直接測定装置を用いて壁面せん断応力の計測を行った流れ場の概要図⁽³⁾を示す．使用された粗面平板の粗さ要素は二次元の矩形形状であり，その配置間隔は局所の流れ方向位置における粗さピッチ比p = (b + w)/k = 4 (wは粗さ要素幅およびbは粗さ要素間溝部幅) とした．kの流れ方向変化率dk/dxは1.25×10^-3とした．この値は，風洞測定部の大きさおよび粗さ高さが一定のk形粗面(k = 3 mm)の結果(相対粗さ高さk/δ = 0.05～0.1，δは境界層厚さ)を参照して決定されている．このとき，δの発達割合dδ/dxのオーダを評価すると，dδ/dx = O(δ/L) = O(10^-2) (Lは流れ方向距離の大きさのオーダ)となり境界層近似の適用が可能となる．

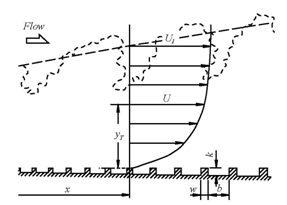
Fig. 4  Flow field, coordinate system and nomenclature

　 図5に壁面せん断応力を主流の動圧で無次元化した局所壁面摩擦抵抗係数c_f値をR_θ数に対して示す．図5中には滑面乱流境界層(以後，滑面流と呼ぶ．) とk形粗面乱流境界層 (以後，k形粗面流と呼ぶ．) の結果を，それぞれ実線と四角印（□および■）で示す．なお，実線の滑面流および■印のk形粗面流の結果は直接測定によるもの ^(5,7) ，□印の結果はk形粗面流の平均速度分布 ⁽⁷⁾ をKrogstadらが提案したVelocity fit method ⁽⁸⁾ に適合して評価されたものである．本粗面流の3箇所のx位置で計測されたc_f値は，本実験範囲内においてx位置ならびにR_θ数によらず一定 (c_f ≒ 0.00826) であり，摩擦パラメータω (= u_τ/U₁) が一定となる．これは，本流れ場が平衡境界層の条件 ⁽⁹⁾ の一つであるdω/dx = 0を満足することを意味する．一方，滑面流とk形粗面流のc_f値は，R_θ数の増加や相対粗さ高さk/δの減少に伴い減少する傾向を示す．詳細は割愛させて頂くが，運動量積分方程式を利用した解析的アプローチから境界層の平均速度分布形状はω= 一定の場合ωのみで，ω≠ 一定の場合ωとdδ/dxに依存することが示されている⁽³⁾．　

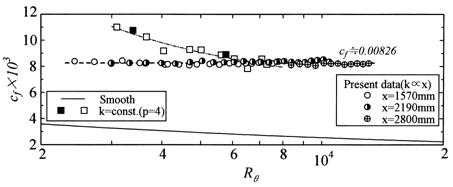
Fig. 5  Local skin friction coefficient

 

4.　終わりに

　 壁面せん断応力の直接測定法に関する原理と計測例について紹介した．乱流境界層の壁面せん断応力の直接測定による研究のアプローチは世界でも稀な方法である．今回紹介した計測法のみでなく，速度や圧力などの計測なども，実験対象となる流れ場に対応したセンサーの利用ならび計測機器条件の設定が必要である．実験装置を使えば必ず計測値が得られるため，得られた計測値の良し悪しを判断するうえで，計測機器に精通することはもちろんのこと，流れ場の性質を理解しておくことは重要である．これらの計測技術の伝承・継承は計測技術レベルの維持や向上において不可欠であり，このような場を借りて壁面せん断応力計測法の情報発信をすることによって興味を持って頂ければ幸いです．

 

文　　　献

(1)	Nagib, H.M. and Chauhan, K.A., “Variations of von Kármán coefficient in canonical flows”, Physics of Fluids, Vol. 20, Issue 10 (2008), pp. 101518 1-10.
(2)	古屋善正，中村育雄，大坂英雄，本田秀雄，“二次元的乱流境界層の横方向不均一性 : 第2報, 壁面摩擦応力と流れ場”,日本機械学会論文集, Vol. 40, No. 339 (1974), pp. 3054-3060.
(3)	亀田孝嗣，望月信介，大坂英雄，檜垣克哉，“完全相似性を満足する粗面乱流境界層の実現とその平均流特性”, 日本機械学会論文集B 編, Vol. 72, No. 717 (2006), pp. 1166-1173.
(4)	Gaudet L. and Winter K.G., “Measurements of the Drag of Some Characteristic Aircraft Excrescences Immersed in Turbulent Boundary Layers”, AGARD CP124 (1973).
(5)	大坂英雄，亀田孝嗣，望月信介，“滑面乱流境界層の局所壁面摩擦抵抗係数と平均量特性”, 日本機械学会論文集B編, Vol. 62, No. 598 (1996), pp. 2230-2237.
(6)	太田圭亮，“逆圧力勾配下に発達する乱流境界層の平均量に関する実験的研究”, 山口大学修士論文(2006).
(7)	大坂英雄，亀田孝嗣，望月信介，“ K形粗面上の乱流境界層の平均量特性”, 日本機械学会論文集B編, Vol. 64, No. 619 (1998), pp. 709-716.
(8)	Krogstad, P.-å., Antonia, R.A., and Browne, L.W.B., “Comparison between Rough- and Smooth-Wall Turbulent Boundary Layers”, Journal of Fluid Mechanics, Vol. 245 (1992), pp. 599-617.
(9)	Rotta, J.C., “Turbulent Boundary Layers in Incompressible Flow”, Progress in Aerospace Sciences, Vol. 2 (1962), pp. 96-129, Pergamon Press.