流れ 2019年3月号 目次
― 特集テーマ:流体工学部門講演会 ―
| リンク一覧にもどる | |
遷音速多段軸流圧縮機における静翼列流れのLES解析
 |
| 齋藤 誠志朗 九州大学 |
はじめに
日本機械学会 第96期 流体工学部門講演会において,光栄にも優秀講演表彰を頂くとともに,ニュースレターにて研究内容を紹介する機会を頂いた.この場をお借りして,選考委員会ならびに日本機械学会の皆様に御礼を申し上げる.本ニュースレターでは,私の研究内容である,大規模数値解析によって遷音速多段軸流圧縮機の静翼列流れ場を高精度に予測した結果について紹介する.
遷音速圧縮機内部流動現象の高精度予測
多段軸流圧縮機は産業用および航空用ガスタービンにおける重要な構成要素の1つである.近年,ガスタービンの熱効率向上に向けて,軸流圧縮機の高圧力比化・高効率化が進められてきた.高圧力比化を従来と同じ段数で達成するためには,翼列当たりの空力負荷を増加させる必要がある.そのため,先進的な高効率ガスタービンの場合,多段軸流圧縮機の初段あたりでは動翼先端の回転周速が超音速となり,圧縮機内部には亜音速流れと超音速流れが混在した遷音速流れ場が形成される.特に圧縮機動翼の翼端付近では強い衝撃波が発生するため,その設計段階において,衝撃波の発生位置だけでなく衝撃波と翼端漏れ渦および翼面乱流境界層との干渉も予測することが求められる.
圧縮機内部の非定常乱流場を正確に予測するためには,LES(Large Eddy Simulation)解析もしくはDNS(Direct Numerical Simulation)解析を実施する必要がある.しかし,本研究の解析対象である遷音速軸流圧縮機の内部には,高レイノルズ数の流れ場が形成されるため,これらの解析手法を適用するためには,きわめて緻密な計算格子が必要となる.また,多段軸流圧縮機の内部では,後流干渉やポテンシャル干渉といった非定常干渉が発生することが知られているが,遷音速多段軸流圧縮機の場合,動翼列で生じた衝撃波が上流側の静翼列に入射することによる干渉(1)(2)等も併せて発生する.数値解析において,これらの非定常干渉の効果を正確に考慮するためには,圧縮機全段・全周を解析対象とする必要があるものの,圧縮機全段・全周を対象として,緻密な計算格子を用いたLES解析もしくはDNS解析を実施することは,現状のコンピュータ性能では困難である.
そこで,本研究では,LES解析とDES(Detached Eddy Simulation)解析(3)を併用した非定常解析を実施することで,現実的な計算時間において圧縮機内部の非定常乱流場を解析することを可能にした.図1に,本研究で使用した計算格子を示す.なお,同図中の圧縮機全体の格子線は3本おきに表示している.本研究では,初段静翼のみ極めて緻密な計算格子を採用しており,初段静翼(図中,青)においてLES解析,それ以外の翼列(図中,緑)でDES解析を実施した.流路当たりの格子点数は,初段静翼において約3,000万点であり,初段静翼以外のDES解析を行う翼列については,初段動翼で約520万点,2段動翼で約410万点,2段静翼で約340万点である.圧縮機全段および全周の総格子点数は約12億点であり,そのうち,初段静翼は約8億点を占めている.なお,壁面上の最小格子幅はすべてy+<1を満足するように十分小さい値を設定した.また,初段静翼は可変静翼であるため,図2に示すように,ハブ側および翼端側に部分クリアランスを設けている.部分クリアランスは上流側と下流側に分かれており,その間はクリアランスのない領域(以下,中実部)となっている.
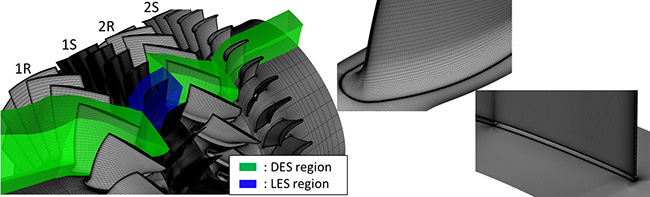
Fig. 1 Computational grid
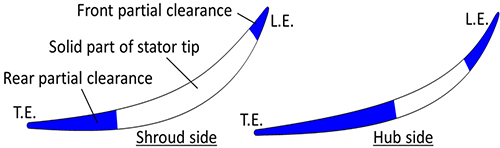
Fig. 2 Shape of partial clearance in first stator
|
|
(a) Limiting streamline, vortical structure |
(b) Vorticity on iso-surface of Q-criterion |
Fig. 3 LES analysis result |
|
初段静翼の流れ場
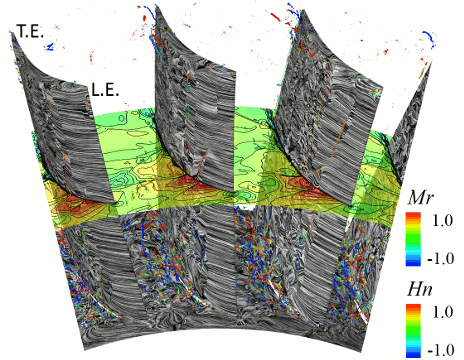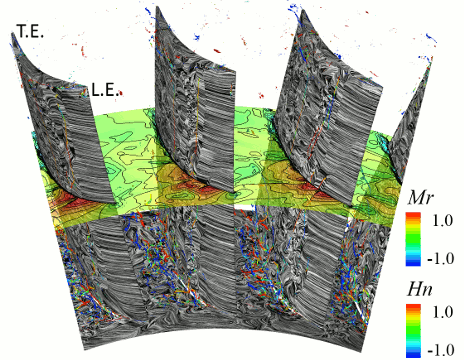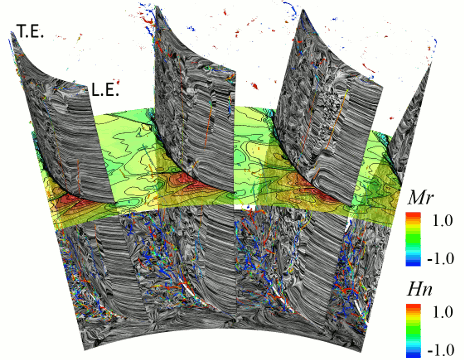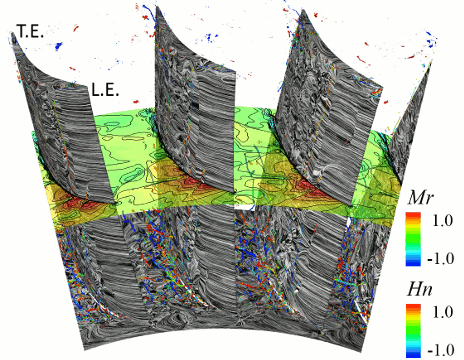
図4に,非定常解析結果に対し,時間平均およびピッチ間アンサンブル平均化処理を行い,1ピッチ分のデータに変換した結果から抽出した,初段静翼負圧面側における流れ場を示す.なお,同図には無次元ヘリシティーで色づけした渦コア(9)およびLIC法を用いて描画した限界流線を表示している.図4から,初段静翼ハブ側において,大規模なハブ・コーナーはく離が発生していることが分かる.ハブ・コーナーはく離領域の内部では,中実部負圧面側においてハブ・コーナーはく離渦が形成されているものの,50%コードから下流側にかけて急激に拡散している.ハブ側の前方および後方に設けられた部分クリアランスからは,それぞれ漏れ渦が発生しており,後方の部分クリアランスに沿った漏れ渦は,50%コード付近から下流側にかけて明確に形成されている.一方で,前方の部分クリアランスからの漏れ渦は,ハブ・コーナーはく離渦の影響で,中実部付近でスパン上方へ持ち上げられるとともに,拡散して消失している.初段静翼のシュラウド側では,圧力面側から負圧面側へ向かうシュラウド面上の二次流れが翼面に到達することで,負圧面上にスパン方向下向きの二次流れが発生しており,この二次流れの影響で,シュラウド側において二次流れ渦が形成されている.翼面上では,20%コード付近において,ほぼ全スパンにわたって大規模なはく離が発生しており,はく離領域の内部には,縦渦状のはく離渦が形成されている.このはく離渦周りの無次元ヘリシティーの値から,はく離領域内の流れは,ハブ側で半径方向上向き,シュラウド側で半径方向下向きに流れており,それらの流れが,30%スパン位置において衝突していることが分かる.また,この衝突が発生するスパン位置からシュラウド側では,上述のはく離の下流側において,再度,広範囲にわたってはく離が発生している.
図5に非定常解析の各時間ステップにおける瞬時の流れ場を示す.なお,同図は,初段静翼負圧面側における渦構造および限界流線に加え,50%スパンにおける衝撃波関数分布および10%スパンにおける渦度分布も併せて表示している.なお,衝撃波関数Fshockは,以下の式により算出した.
|
|
(1) |
|
|
(2) |
ここで,Pscは各格子点における静圧,Psiは考慮している格子点に隣接する参照点における静圧を表す.
図5から,いずれの時間ステップにおいても,20%コード付近から下流側にかけて,翼面近傍に多数のはく離渦が発生していることが分かる.また,衝撃波関数分布と翼面上のはく離の位置を比較すると,翼面上ではく離渦が形成されている位置は,2段動翼からの衝撃波が翼面上で反射している位置に対応しており,2段動翼からの衝撃波が翼面境界層と干渉することで,はく離が発生していることが確認できる.また,初段静翼の翼間に入射した衝撃波は,翼面上での反射を繰り返しながら上流側へ伝播しており,それに伴って,翼面上のはく離の位置も上流側へ移動している.衝撃波の間隔は,上流側に向かうにつれ狭まっており,特に20%コード付近では,非常に密接して存在していることが確認できるが,これは,20%コード付近において負圧面側の流体が音速に近い速度まで増速し,衝撃波の伝播速度が低下したためであると考えられる.また,20%コード付近では,伝播速度の遅い衝撃波によって,翼面上にはく離が密接して発生するため,図4に示す時間平均流れ場においても,20%コード付近において,はく離が確認できたと考えられる.
ハブ・コーナーはく離領域に着目すると,図4に示す時間平均流れ場では,ハブ面から巻き上がる1つのハブ・コーナーはく離渦が発生するが,瞬時の流れ場では,はく離領域内に非常に多数のはく離渦が発生し,それらが互いに干渉することで,その位置や形状を時間的に大きく変化させている.また,ハブ・コーナーはく離領域の内部には,渦度の高い領域が複数に分かれて存在しており,それらが時間の経過とともに下流側へ移流している.
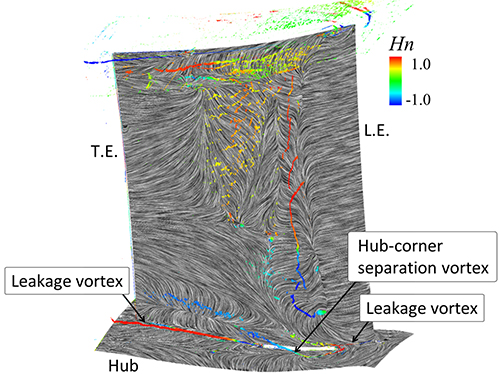
Fig. 4 Time-averaged flow field in first stator
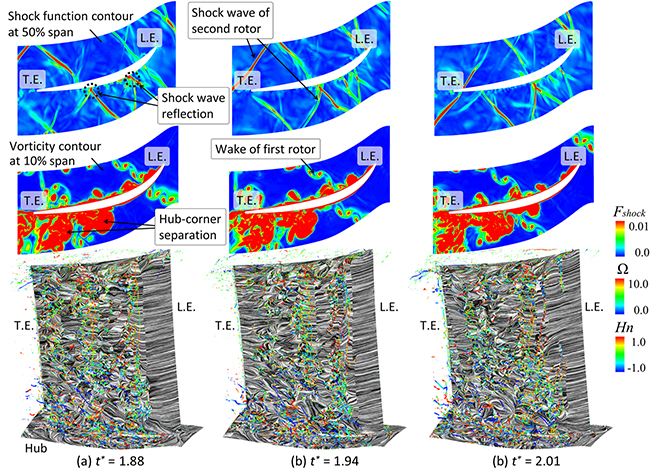
Fig. 5 Instantaneous flow field in first stator
結言
本研究では,2段遷音速軸流圧縮機の全段および全周を対象として,LES解析とDES解析を併用した大規模非定常解析を実施し,初段静翼における複雑乱流場の流れ構造の調査を行った.得られた知見は,以下の通りである.
| (1) | 初段静翼負圧面ハブ側において大規模なハブ・コーナーはく離が発生し,時間平均流れ場では,中実部負圧面側にハブ・コーナーはく離渦が1つ形成される.一方,瞬時の流れ場では,ハブ・コーナーはく離領域内に多数のはく離渦が発生し,それらが互いに干渉することで,その位置や形状を時間的に大きく変化させる. |
| (2) | 初段静翼の負圧面上では,2段動翼からの衝撃波が初段静翼の翼面で反射する際に翼面境界層と干渉することで,境界層はく離が発生する.特に20%コード付近では,衝撃波の伝播速度が低下する影響で,翼面上のはく離が密接して発生する結果,時間平均流れ場においても,ほぼ全スパンにわたってはく離が形成される. |