流れ　2019年3月号　目次

―　特集テーマ：流体工学部門講演会　― 巻頭言 （橋本，松田，朴） 民間単独での観測ロケット開発と打上げとその後の超小型衛星打上げロケット開発状況 稲川 貴大（インターステラテクノロジズ株式会社） 一様吹出し制御による翼面摩擦抵抗低減効果の実験的定量評価 江藤 薫子，近藤 佑亮，深潟 康二（慶應義塾大学），徳川 直子（宇宙航空研究開発機構） 受動吹出し制御による翼面摩擦抵抗低減の風洞実験 廣川 詩歩，江藤 薫子，近藤 佑亮，深潟 康二（慶應義塾大学），徳川 直子（宇宙航空研究開発機構） 翼に渦が干渉する場合の翼周りの流れと発生する空力騒音に関する研究 小林 典彰（東京大学） 遷音速多段軸流圧縮機における静翼列流れのLES解析 齋藤 誠志朗（九州大学） WALEモデルを用いた円管内乱流のLESにおける格子解像度の影響 岩佐 大器，難波江 佑介，深潟 康二（慶應義塾大学） 流れの夢コンテストに参加して 寺田 智美（北海道大学）   水面制御装置を用いたゴミの分別 本間 俊貴（明星大学） 　｜　リンク一覧にもどる　｜

 

WALEモデルを用いた円管内乱流のLESにおける格子解像度の影響

岩佐 大器 慶應義塾大学 難波江 佑介 慶應義塾大学 深潟 康二 慶應義塾大学

はじめに

　平成30年11月の室蘭の蓬崍殿で開催された第96期流体工学部門講演会において研究発表⁽¹⁾を行い，光栄にも日本機械学会流体工学部門優秀講演表彰を頂いた．また，ここにニュースレターとして我々の研究を紹介させていただく機会を頂いた．この場を借りて選考委員会の皆様および日本機械学会の皆様に御礼を申し上げるとともに，講演発表内容を紹介させていただく．

非常に粗い計算格子幅における数値シミュレーション

　CAE (Computer Aided Engineering) は自動車エンジンの開発において欠かせないツールである．国家プロジェクトの一つである「戦略的イノベーション創造プログラム（SIP）」では最大熱効率50%及び二酸化炭素排出量30％削減という目標の達成に向け，自動車エンジンの3次元燃焼解析ソフトウェア（HINOCA）の開発が進められている⁽²⁾．HINOCAは数多くの物理モデルが統合されている数値シミュレーションソフトウェアであるため，エンジン筒内の一連の物理過程を再現することを可能とするが，現実的な計算時間内に数値シミュレーションを完了させるためには粗い計算格子幅を用いることが避けられない．HINOCAにおけるLES（Large Eddy Simulation）のSGS（Subgrid Scale）モデルとしてはWALEモデル（wall-adapting local eddy-viscosity model）⁽³⁾が使用されているが，これはWALEモデルには壁面距離の算出なしで壁面漸近挙動を再現できる強みがあるため⁽⁴⁾である．

　これまでにもLESにおける格子解像度の研究は数多くされてきている⁽⁵⁾が，その多くが主流方向およびスパン方向（周方向）の格子解像度に関するものであり，壁面垂直方向における格子解像度について精査している研究はない．ゆえに非常に粗い格子幅においては，WALEモデルにおける渦粘性係数の壁面漸近挙動の再現性も不明であり，カノニカルな系における包括的な格子依存性の調査が必要であると言える．そこで本研究では， WALEモデルを用いて円管内乱流における格子解像度の影響の調査することを目的とした．

数値解析手法

　本研究ではFig. 1に示すような円管内乱流を解析対象とした．支配方程式はTop-hatフィルタによってフィルタリングされた三次元の非圧縮性流れに対する連続の式とナビエ・ストークス方程式である．本研究では流量一定条件を仮定し，バルク平均速度に基づくレイノルズ数をRe_b = 5300とした．結果として得られるべき摩擦レイノルズ数 Re_τ は約180である．LESのSGSモデルにはWALEモデルを使用し，主流方向には周期境界条件を，壁面には滑りなし境界条件を適用している．

Fig. 1: Computational domain for numerical simulations of a turbulent pipe flow.

結果および考察

　Figure 2に，半径方向，周方向および主流方向の格子点数が (N_r, N_θ, N_z) = (6, 64, 64) の場合の平均速度分布および速度変動のRMS値の分布を示す．Fig.2(a) での不等間隔格子の場合では，壁面垂直方向に格子数が6点しかないにもかかわらず，速度分布はDNSと一致していることが確認できる．このときの壁最近点位置は y₁⁺ = 4.4 であり，壁面垂直方向における計算格子間隔に対する感度は，従来考えられてきたものよりもはるかに低いことがわかった．しかし，等間隔格子の場合では，壁面最近点での速度が，粘性底層での速度分布を表す u⁺ = y⁺ 上にあることが確認できる．Fig. 2(b)のRMS値を見ると，壁面垂直方向成分は良い一致を示しているものの，主流方向成分は，DNSより大きい．これは各速度変動成分間でのエネルギーの再分配が十分に再現できていないことが原因と考えられるが，これはLESにはよく見られる結果である．しかし，等間隔格子における壁面最近傍点における主流方向速度のRMS値は本来ピーク値をさすべきであるにもかかわらず，低い値を示した．Fig. 3にDNSおよび壁面垂直方向の格子数が6点の不等間隔格子の場合におけるストリークを示す．Fig. 3(b) で観察されるストリークの様相は定性的にはDNSと類似しているが，ストリーク長さはDNSよりも非常に短いことが確認できる．よって，速度分布やRMSといった統計量はDNSと一致しているものの，ストリークのような詳細な乱流構造は異なっていることが確認できる．

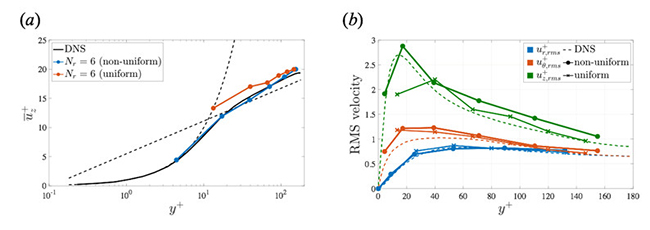
Fig. 2: Turbulent statistics using only 6 points with uniform or non-uniform grid spacings in the wall-normal direction. (a) Mean streamwise velocity profiles (solid lines with markers) and the law of the wall (dashed line); (b) RMS velocity fluctuations.

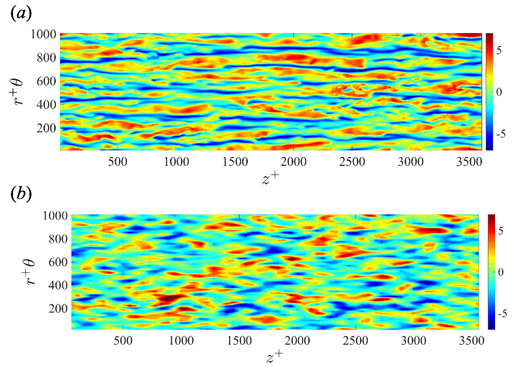
Fig. 3: Instantaneous streamwise velocity fluctuation contours at y⁺ = 20 in the turbulent pipe flow. (a) DNS; (b) LES in the case of (N_r, N_θ, N_z) = (6, 64, 64).

　Figure 4に，周方向および主流方向の格子点数が (N_θ, N_z) = (64, 64) おいて，壁面最近傍の計算点の位置を変化させた場合の，その点上における主流方向速度および主流方向速度のRMS値の散布図を示す．Fig. 4(a)では，壁面最近傍点における速度は u⁺ = y⁺ 上に分布していることがわかる．また，最近傍点が y⁺ < 6 の場合はDNSと一致し，それ以上壁面から離れると，Fig. 2(a)の等間隔格子の場合のように分布することがわかる．よって，粗い格子幅の条件でDNSに即した速度分布を得るためには，少なくとも第1点目を y⁺ < 6 に設定する必要がある．一方，Fig. 4(b)も同様に y⁺ < 6 の場合ではDNSの分布に沿うことが確認できる．しかし，それ以上離れるとRMS値は徐々に減少し，バルク領域での流動に大きな影響を与えるRMSのピーク値を第1点目で再現することが不可能であることがわかった．

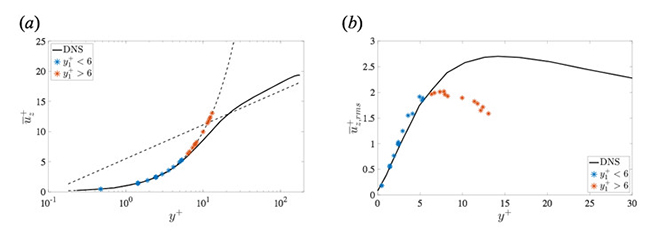
Fig. 4: Relationship between the wall-normal location of the first grid point from the wall and the resultant values of turbulent statistics there: (a) mean streamwise velocity; (b) RMS streamwise velocity fluctuation.

おわりに

　本研究では，WALEモデルを用いた円管内乱流のLESにおける格子解像度依存性を調査し，WALEモデルでは壁面垂直方向における計算格子がわずか6点であっても，DNSと比べて妥当な乱流統計量が得られることを示した．また，第１点目における乱流統計量はその位置に大きく依存し，格子点を y⁺ < 6 に設定することにより，平均速度分布およびRMS値に関して良い結果を得られることがわかった．ただし，本研究における結果は十分なエネルギー保存性を持つ離散化手法⁽⁶⁾を用いた場合での結果であり，そうでない場合で少ない計算点数を用いた場合には，妥当な統計量どころか計算が発散する可能性も少なくないことを申し添えておく．

謝辞

　本研究は総合科学技術・イノベーション会議のSIP（戦略的イノベーション創造プロジェクト）「革新的燃焼技術」（管理法人：JST）の一環として実施されたものです．末筆ではありますが，SIPプロジェクトにおいてお世話になりました先生方，当日会場にてご聴講いただいた貴重なご意見を頂きました皆様，選考委員会の皆様，並びにニュースレター執筆の機会を与えてくださいました日本機械学会流体工学部門の関係者の皆様に感謝申し上げます．

参考文献

(1)	岩佐 大器，難波江 佑介，深潟 康二，「WALEモデルを用いた円管内乱流のラージ・エディ・シミュレーションにおける格子解像度の影響」，日本機械学会第96期流体工学部門講演会，室蘭，2018年11月29日-30日，Paper OS15-7．
(2)	Mizobuchi, Y., “Development of automotive engine combustion simulation software “HINOCA”,” Journal of the Combustion Society of Japan, Vol. 58, No. 186, (2016), pp. 191-196.
(3)	Nicoud, F. and Ducros, F., “Subgrid-scale stress modelling based on the square of the velocity gradient tensor,” Flow, Turbulence and Combustion, Vol. 62, (1999), pp. 183-200.
(4)	桑田 祐丞，須賀 一彦，「正方形角柱群内乱流の LES による体積平均乱流輸送方程式の考察」，日本機械学会論文集（B 編）, Vol. 79, No. 805, (2013), pp.1752-1763.
(5)	Meyers, J. and Sagaut, P., “Is plane-channel flow a friendly case for the testing of large-eddy simulation subgrid-scale models?,” Physics of Fluids, Vol. 19 (2007) , 048105.
(6)	Fukagata, K. and Kasagi, N., “Highly energy-conservative finite difference method for the cylindrical coordinate system,” Journal of Computational Physics, Vol. 181 (2002), pp. 478-498.