流れ 2020年2月号 目次
― 特集テーマ:流体工学部門講演会 2月号 ―
| リンク一覧にもどる | |
希薄気体力学における移動境界問題について
辻 徹郎 京都大学 |
はじめに
日本機械学会第97期流体工学部門講演会にて基調講演の機会をいただき,大変光栄に思います.今回のお呼びいただけたのは,2017年度の日本機械学会奨励賞(研究)受賞がきっかけと伺っております.流体工学部門のみなさま並びに第97期流体工学部門講演会実行委員のみなさまには,この場を借りて深く御礼申し上げます.本稿では,講演内容である希薄気体力学における移動境界問題(1)(2)について,簡単に説明させていただきます.これは,私の博士論文の内容が主となっており,流体工学部門のみなさまに紹介できることを大変うれしく思います.
背景
気体分子の平均自由行程l(図1)が流れの代表長さLに比べて無視できない程度に大きいとき,気体は希薄であると言います.このような気体(希薄気体,分子気体)を解析する枠組みが希薄気体力学です.流れを特徴づける代表的なパラメータはKnudsen数と呼ばれ,Kn = l/L で定義されます.気体の巨視的な連続体仮定に基づく通常の流体力学の枠組みは Kn → 0 の極限に対応していますが,lが大きい低圧気体やLが小さいマイクロ流れではKnが有限の値を取るため,気体の振舞いの解析には希薄気体力学を用いる必要があります.本稿に示す研究では,希薄気体力学における移動境界問題を精密な数値解析手法で調べ(1),その応用として希薄気体中を振動する1次元線形振子の減衰則を明らかにしました(2).特に,後者は振子と気体の運動が連成する移動境界問題で,例えばマイクロ共振器の流体解析への応用が期待されます.詳細は参考文献に譲るとして,ここでは主要な結果を概説するにとどめます.
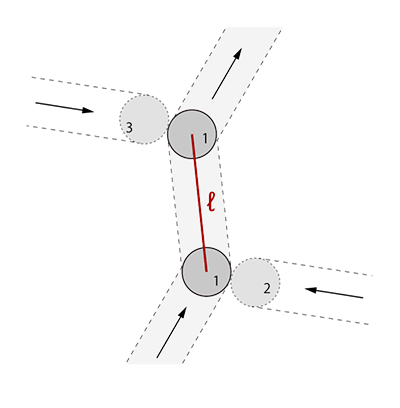
Figure 1 The definition of mean free path of gas molecules.
希薄気体力学特有の困難さ:速度分布関数の特異性
希薄気体力学の支配方程式はBoltzmann方程式あるいはそのモデル方程式で,未知関数は気体分子の速度分布関数 f(x, v, t) です.ここで,xは位置ベクトル,vは分子速度,tは時間です.希薄気体に対する移動境界問題の難しさは,f にいくつかの特異性が生じることにあります.ここではもっとも代表的な特異性である不連続について簡単に紹介します.図2に,定常な境界値問題の模式図を示します.境界上のある点とそこでの法線ベクトルnに注目すると,v・n < 0 となるような分子は境界へ入射し,v・n > 0 となるような分子は境界を反射します.一般に,境界に衝突した気体分子は境界を構成する原子と相互作用し,その結果として反射後の分子速度が決定されます.一方,v・n < 0 における速度分布関数は支配方程式から決定されるため,図2に示すように境界上のf はv・n = 0 で不連続となります.このように境界上で発生した不連続は,気体分子の運動経路(Boltzmann方程式の特性曲線)に沿って気体領域中に伝播していきます.希薄気体の振舞いを精密に解析する場合は,この不連続を適切に捉える数値解析手法が必要です.定常問題に対しては,境界形状が定まれば(x, v) 空間における不連続の位置が決まります.しかし,移動境界問題では,不連続の位置が境界運動とともに変化し,さらに新たな不連続が連続的に生成されていきます.これらの不連続をすべて適切に処理する必要があるため,希薄気体の移動境界問題の精密な数値解析はこれまで行われていませんでした.文献(1)では,空間的1次元の問題に限定しましたが,特性曲線法をもとにした数値解析により,速度分布関数の不連続を含む特異性をすべて捉えた数値解の構築に成功しました.
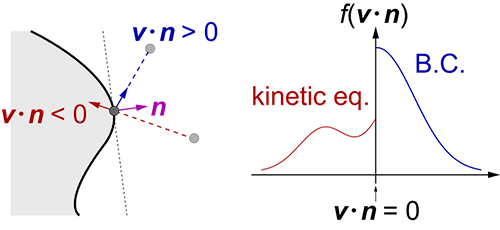
Figure 2 Gas molecules impinges on the boundary with a velocity v・n < 0 and are reflected with a velocity v・n > 0. The velocity distribution function on the boundary is discontinuous at v・n = 0. The discontinuity produced on the boundary can propagate into the gas domain along the characteristic curve.
速度分布関数の振舞い
以下では,詳しい記号の定義は文献を参照していただくとして,無次元化した変数を用いて結果を紹介します.境界は無限に広い平板で,平板はその垂直方向に振幅1で定常振動するとします.図3は振動の7周期目における速度分布関数gの様子です.実線は今回提案した特性曲線法の結果で,シンボルは通常の差分法を用いたときの計算結果です.(a), (b), (c)はそれぞれ,Knudsen数に相当するパラメータKが∞, 10, 1の場合を表しています.上段と下段は,それぞれ比較的境界に近い場所と遠い場所に対応しています.図から分かるように,K = ∞では,速度分布関数はいくつかの不連続と急峻な構造を持ちます.ここで,K = ∞ の場合は,気体分子同士の衝突が無視できるほどに希薄な場合に相当することに注意してください.一方,シンボルで示す通常の差分法ではこれらの構造を適切に捉えられていません.K = 10, 1と,Kが小さくなるにつれて,気体分子間の衝突の影響のおかげで,不連続と急峻な構造は緩和されていきます.そのため,K = 1の場合では,特性曲線法と差分法は比較的良い一致を示します.密度,流速,平板に働く力などの巨視的な物理量はすべて速度分布関数のモーメントとして計算されるため,速度分布関数の構造を適切に捉えていない計算手法では,特にKが大きいときに,信頼性が低くなると言えます.
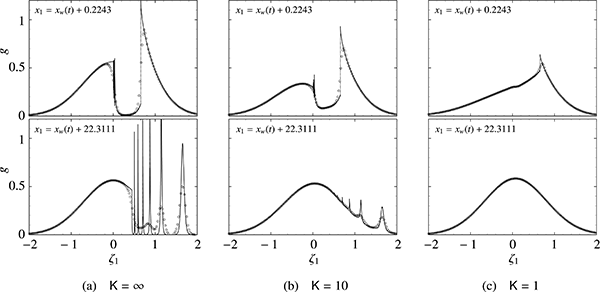
Figure 3 Velocity distribution functions of gas molecules in moving boundary problems. The boundary is an infinite plate oscillating in its perpendicular direction with the non-dimensional amplitude unity. g = g(x1, ζ1, t) is the non-dimensional marginal velocity distribution function, x1 and ζ1 are the non-dimensional position and molecular velocity in the direction of the oscillation of the plate, respectively, xw(t) is the non-dimensional position of the plate, and K is the parameter of the order of Knudsen number. Solid lines are obtained using the method of characteristics, while symbols are obtained by a standard finite-difference scheme. The former captures the details of the velocity distribution function including discontinuities but the latter fails. This figure is reprented from Ref. (1) under the permission of Elsevier.
連成移動境界問題:線形振子の減衰
連成移動境界問題の例として,線形振子の減衰則を調べた結果を紹介します(2).この問題は,マイクロ共振器の振動に対する,希薄気体力学を基にした流体解析の単純な例と言えます.ここでは特に,どのように振子が静止状態に近づいていくかに注目しました.前節と同様に,空間1次元の問題すなわち無限に広い平板の垂直方向への運動を考えます.平板には復元力が働いているため,気体が及ぼす抵抗により平衡位置からのずれxwは時間の経過とともに減衰していきます.図4は,平板の初期変位xw0 = 0.1と初速度vw0 = 0に対するxwの時間発展の様子です.ここで,Mは無次元化した平板の質量に相当するパラメータで,K = 0.4, 1, 2および5の場合を調べました.(a)-(c)は変位の振幅|xw| を,(d)-(f)は|xw|の両対数スケールにおける傾きαを表します.|xw| がtαに比例するとき,α = nとなることに注意してください.図4が示すように,振子の減衰則は時間が十分に経過したあと,|xw| ≈ Ct -3/2 で表されることが分かります.K → ∞ の場合は異なる減衰則|xw| ≈ Ct -2となることが知られているので,これらの結果より,分子間衝突の影響が振子の減衰則に定性的な影響を与えることが明らかになりました.マイクロ構造体の振動を解析する場合,振動運動の減衰に対するこのようなKnudsen数の依存性を考慮に入れてデータを解析する必要があると考えられます.

Figure 4 log10|xw| versus log10 t for long times at several K for xw0 = 0.1, vw0 = 0. (a) M = 2, (b) M = 1, and (c) M = 0.5. Panels (d), (e), and (f) show, respectively, the gradient of the curves in panels (a), (b), and (c). This figure is reprented from Ref. (2) under the permission of American Physical Society.
おわりに
本稿では希薄気体力学における移動境界問題について,簡潔にご紹介させていただきました.希薄気体力学はKnudsen数が小さい極限として通常の流体力学を含有しており,低圧気体やマイクロ流れだけでなく,通常の流体力学の拡張という文脈でもさまざまな研究が進められています.本稿が多少なりとも読者に希薄気体力学について興味を持っていただく機会になっていれば幸いです.


