流れ　2020年2月号　目次

―　特集テーマ：流体工学部門講演会　２月号　― 巻頭言 （橋本，松田，朴） 希薄気体力学における移動境界問題について 辻 徹郎（京都大学） 各種噴流現象、及びはく離流れの流動制御 社河内 敏彦（三重大学） チャネル乱流における機械学習3次元超解像解析 深見 開，深潟 康二（慶應義塾大学）平 邦彦（UCLA） プラズマアクチュエータを用いた振動角柱周りの流れの制御 小那覇 千尋（豊橋技術科学大学） 音に夢を重ねて 福嶋 拓海（東京理科大学） 　｜　リンク一覧にもどる　｜

 

チャネル乱流における機械学習3次元超解像解析

深見 開 慶應義塾大学	深潟 康二 慶應義塾大学	平 邦彦 UCLA

1.　はじめに

　第97回流体工学部門講演会において講演発表^[1]を行い，日本機械学会流体工学部門優秀講演表彰を頂きました．この場をお借りし，流体工学部門の皆様に御礼申し上げます．本ニュースレターでは，講演内容である，機械学習超解像を用いた乱流場の再構築について紹介させて頂きます．

2.　背景および目的

　流体力学分野における時空間高解像データは，これまでの流体力学の進歩に大きく貢献してきた．実際に，実験流体力学における粒子画像流速測定法の発達や，数値流体力学における直接数値シミュレーションの高解像化は現象理解や理論構築に役立ってきた．このような背景から，これまで多くの研究者によって、限られたデータから高解像の時空間データを推定する手法が提案されてきた．Chavailer et al. ^[2] は，カルマンフィルタをチャネル流に適用し，壁面の情報からチャネル中心部の流れのデータを推定することを試みた．Linear Stochastic Estimationを同様の問題設定に応用した例も報告されている^[3]．これらのアプローチは確かに流体力学分野へのデータ推定法の適用可能性を示唆してきたが，強い非線形やカオスを含む乱流への適用は未だにチャレンジングな課題である．データの推定や再構築は，流体力学分野に留まらずデータサイエンス分野でも喫緊の課題である．特に，低解像の画像データから高解像データを構築することを試みる，超解像解析は非常に注目を集めている手法として挙げられる．近年，超解像解析と機械学習を組み合わせた手法が画像処理分野で提案され，高解像データを得るための一つの手法として，非常に高い能力を示している^[4]．筆者らのグループは，この機械学習超解像解析を2次元一様等方性減衰乱流に適用し，機械学習モデルにより再構築された流れ場が，渦度場の可視化やエネルギースペクトルの観点から，高解像の直接シミュレーションデータと良好な一致を示すことを報告した^[5,6]．加えて，近年時間方向のデータ再構築手法として，Inbetweening^[7] に注目が集まっている．Inbetweeningとは，ビデオを始めとした時系列データの両端からその間を時間的内挿する手法である．本研究では，実用的な応用例としてチャネル乱流を題材に，3次元流れ場に対して，超解像手法およびInbetweeningを組み合わせた，時空間超解像解析フレームワークを適用し，提案手法の更なる応用可能性を様々な乱流統計量の観点から調査する．

3.　手法

3・1　時空間超解像解析
本研究における，時空間超解像解析のコンセプトを，二次元減衰乱流を例としてFig. 1に示す．まず時空間低解像データq(x_LR, t_LR) を空間超解像モデルF_xに入力し，空間的高解像データq(x_HR, t_LR) を得る．即ち，q(x_HR, t_LR) = F_x (q(x_LR, t_LR)) と定式化される．次に，時刻t = nΔtとt = (n+k)Δt の2時刻において空間的に再構築された瞬時場がInbetweeningモデルF_tに入力され，t = (n+1)Δtからt = (n+k-1)Δt までの流れ場が時間的内挿により再構築される．このプロセスを通じて，時空間高解像データq(x_HR, t_HR) を得る．即ち，本研究における問題設定は，

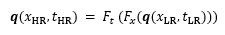(1)

と定式化される.

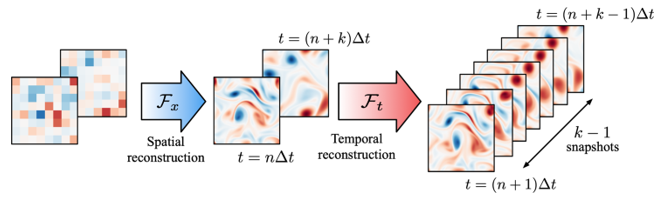
Fig 1.  Spatio-temporal super resolution reconstruction of two-dimensional turbulence.

3・2  機械学習モデル
本研究では，筆者ら^[5] が提案した Hybrid downsampled skip-connection multi-scale (DSC/MS) model を3次元データのために拡張したものを機械学習モデルとして使用する．提案された手法は，画像分野で近年広く使われている 畳み込みニューラルネットワーク (CNN)^[8] をベースとしている．CNNはフィルタと呼ばれる特徴検出器を使用し，与えられた入力ベクトルxから望まれる出力yを得るための重みwを訓練プロセスを通じて学習する．本研究では，入力である低解像データq_LRから，出力である高解像データq_HRを生成する機械学習モデルFを構築することを試みるので，訓練プロセスの目的は

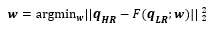(2)

と表される．式 (2) に示す通り，本研究ではL₂ノルムを誤差関数に使用する．入出力ベクトルqは，特徴ベクトルと呼ばれる．本研究では速度場データ[u, v, w]^Tをqとする．なお，詳細は後ほど述べるが，空間低解像データは入力解像度に応じ，1つの値を8×8×8，または16×16×16の領域にコピーすることにより、高解像データと同じ画像サイズに変換して入力に用いる．機械学習モデルの詳細に関しては，Fukami et al.^[5]を参考されたい．

3・3　題材：チャネル乱流
本研究では，チャネル乱流の直接数値シミュレーション (DNS) を訓練データとして用いる^[9]．支配方程式は，非圧縮の連続の式およびナビエ・ストークス方程式，

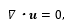	(3)
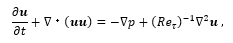	(4)

である．ここでu=[u v w]^τ は主流方向 (x), 壁面垂直方向 (y)，スパン方向 (z)の速度成分，p は圧力，t は時間である． は摩擦レイノルズ数であり，摩擦速度 u_τ，動粘性係数 ν，チャネル半幅 δ で定義される．また支配方程式中の物理量は，これらにより無次元化されている．本研究では，Reτ = 180 として，圧力勾配一定条件下で計算し得られたデータを用いる．計算領域および計算格子数はそれぞれ (L_x, L_y, L_z) = (4πδ,2δ,2πδ)，(N_x, N_y, N_z) = (256, 96, 256)とし，等間隔格子を用いる．境界条件は壁面で滑りなし条件，主流方向とスパン方向には周期境界条件を適用する．このチャネル乱流では，x および z 方向は一様であること，y 方向の統計量は対称的であることを考慮し，訓練データとして用いる計算領域および計算格子数は，L_x^*=2πδ, x ∈[πδ, 3πδ], L_y^*=δ, y ∈ [0, δ], L_z^*=πδ, z∈ [0.5πδ, 1.5πδ])，(N_x^*, N_y^*, N_z^*) = (128, 48, 128) とする．本研究では機械学習モデルへの入力として，空間高解像データに平均プーリングを施したものを低解像データとして使用する．本研究では 8×8×8 および 16×16×16 プーリングを施すことで，16×6×16（medium resolution）および 8×3×8（low resolution）格子の空間低解像データを使用する．

4.　結果および考察

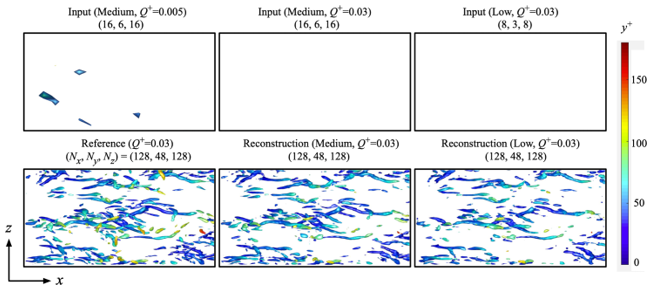
Fig 2.  Spatial super resolution reconstruction of turbulent channel flow.

まず空間超解像に関して，再構築された速度場から計算された速度勾配テンソルの第二不変量（Q値）の等値面のx-z平面をFig. 3に示す．図に示す通り，Q⁺ = 0.03における低解像流れ場では渦核が確認されないことから，入力データが非常に粗いことが観察される．ここで，図に示す通り（Q⁺= 0.005），これらの流れ場において閾値が低い場合は小さな構造が確認されることに注意されたい．再構築された場に注目すると，機械学習モデルによって流れ場は再構築され，また答えとなるDNSの瞬時場と非常に良い一致を示す．

　次に，これらの空間的に再構築された流れ場は，Fig. 1で示した通り，Inbetweeningモデルに入力される．ここで，本研究ではチャネル乱流の壁面付近における時間二点相関に基づき，最初と最後のスナップショット間の時間幅としてMedium および Wide タイムステップを考える．ここでは入力する空間低解像データとして，medium resolutionを使用する．問題設定および再構築の結果をFig. 3にまとめる．図に示す通り，medium タイムステップでは，時間方向に流れ場は再構築されDNSと良い一致を示す．一方，wideタイムステップでは時間方向の粗さを原因に，DNSのような渦核が再構築されない．以上より，提案されたモデルは，相関がある程度高い時間幅であれば時空間超解像が可能である．

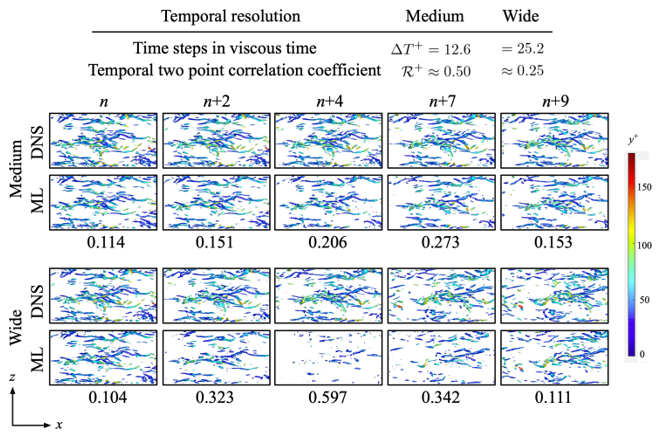
Fig 3.  Spatio-temporal super resolution reconstruction of turbulent channel flow. The listed values indicate the L₂ error.

5.　結言

　本研究では，機械学習3次元超解像解析をチャネル乱流へ適用し，時空間超解像解析フレームワークを構築した．格子数128×48×128のチャネル乱流場が，非常に粗い低解像データから機械学習モデルにより再構築され，再構築された流れ場はDNSデータと良好な一致を示すことが確認された．また相関が低くない時間幅であれば，Inbetweeningと空間超解像を組み合わせることで，時空間的な流れの再構築が可能であることを示した．チャネル乱流における3次元空間超解像については，Fukami et al.^[10]を参照されたい．

謝辞

　本研究は，JSPS科研費基盤研究(A)「機械学習による乱流ビッグデータの特徴抽出手法の構築」(慶大・深潟，18H0375)，US Army Research Office (UCLA・平，W911NF-17-1-0118), および US Air Force Office of Scientific Research (UCLA・平，FA9550-16-1-0650) の助成を受けたものです．加えて，村田高彬，長谷川一登，中村太一，森本将生の各氏（慶大）に深く感謝いたします．

文献

[1]	深見 開，深潟 康二，平 邦彦，「3次元チャネル乱流における機械学習超解像解析」，日本機械学会第97期流体工学部門講演会，豊橋，2019年11月7日-8日，Paper OS8-01 (2019).
[2]	Chevailier, M., Hoepffner, J., Bewley, T., R., and Henningson D., S., “State estimation in wall-bounded flow systems. Part 2. Turbulent flows”, J. Fluid Mech., Vol. 552, pp. 167-187 (2006).
[3]	Suzuki, T., and Hasegawa, Y., “Estimation of turbulent channel flow at Reτ=100 based on the wall measurement suing a simple sequential approach”, J. Fluid Mech., Vol. 830, pp. 760-796 (2017).
[4]	Dong, C., Loy, C. C., He, K., and Tang, X., “Image super-resolution using deep convolutional networks”, IEEE transactions on pattern analysis and machine intelligence, Vol. 38, No. 2, pp. 295-307 (2016).
[5]	Fukami, K., Fukagata, K., and Taira, K., “Super-resolution reconstruction of turbulent flows with machine learning”, J. Fluid Mech., Vol. 870, pp. 106-120 (2019).
[6]	深見 開，深潟 康二，平 邦彦，「2次元流れ場への機械学習超解像の応用」，ながれ，Vol. 38, pp. 395-398 (2019).
[7]	Li, Y., Roblek, D., and Tagliasacchi, M., “From here to there: Video inbetweening using 3D convolutions”, arXiv preprint, arXiv:1905.10240 (2019).
[8]	Lecun, Y., Bottou, L., Bengio, Y., and Haffner, P., “Gradient-based learning applied to document recognition”, Proc. IEEE, Vol. 86, No. 11, pp. 155-166 (2006).
[9]	Fukagata, K., Kasagi, N., and Koumoutsakos, K., “A theoretical prediction of friction drag reduction in turbulent flow by superhydrophobic surfaces”, Phys. Fluids., Vol. 18, No. 051703 (2006).
[10]	Fukami, K., Fukagata, K., and Taira, K., “Assessments of supervised machine learning for fluid flows”, Theor. Comp. Fluid Dyn., in review (2019).