流れ 2020年3月号 目次
― 特集テーマ:流体工学部門講演会 3月号 ―
| リンク一覧にもどる | |
進行波状弾性壁面を有する円管内乱流の抵抗低減効果
中澤 誠也, |
1.はじめに
第97期日本機械学会流体工学部門講演会にてポスター発表を行い,光栄にも若手優秀講演フェロー賞を頂き,また,ニュースレターとして我々の研究を紹介させていただく機会を頂いた.この場をお借りし,流体工学部門の皆様に御礼を申し上げる.本報では,部門講演会での発表内容である,進行波状弾性壁面を有する円管内乱流の抵抗低減効果について紹介させて頂く.
2.研究背景および目的
パイプラインなどの流体輸送機器における流れの多くは乱流であり,摩擦抵抗は層流に比べて著しく増加する.したがって,多くの駆動力を消費する摩擦抵抗を低減させることは,省エネルギ化において重要である.乱流中の摩擦抵抗低減手法の一つに進行波制御がある.進行波制御とは,物体壁面に下流へと進行する波を発生させる手法である.
これまで,直接数値計算(Direct Numerical Simulation, DNS)によって,進行波制御による抵抗低減メカニズムが検証されてきた.平行平板間乱流(1)および円管内乱流(2)の進行波制御において,それぞれ最大69%および60%の抵抗低減と渦の抑制に伴う再層流化が確認されている.一方,室内実験に関しても,平板上で魚の遊泳運動を模擬することにより,乱流境界層の強い層流化の傾向を確認した例(3)や,円管内乱流において壁面に周方向の進行波を発生させることで,約33%の抵抗低減を確認した例(4)がある.しかしながら,円管内乱流においては壁面における流れ方向の進行波の発生や流れ場の計測が困難であるため,進行波制御による抵抗低減効果を実験的に評価した例は少ない.
本研究では,円管内乱流における進行波制御時の差圧計測と,レーザドップラ速度計測(Laser Doppler Velocimetry, LDV)による流れ場の計測を行うことで,進行波制御による抵抗低減効果を実験的に評価することを目的とする.
3.実験装置および実験方法
図1に実験装置測定部付近の概略図を示す.進行波を実現するため,円管は厚さ0.3 mmのシリコーンゴムシートで作成した.制御による円管の振幅は拡大して図示した.作動流体には空気を用い,開放型の流路を作成した.円管の内径は2R = 27 mmであり,ゴムのたわみを防ぐため,地面に対して鉛直に円管を配置した.また,テストセクション長さは110Rとした.
円管の上流側にピエゾアクチュエータ(Cedrat製,APA-1000L)を周方向に等間隔に3台設置し,下流方向に振動を与えた.アクチュエータの入力は電圧と周波数であり,それぞれ35 Vと150 Hzとした.
LDV計測により円管内の主流方向流速の計測を行った.LDVプローブのレンズの焦点距離は350 mmであり,波長561 nmのレーザを用いた.検査体積の大きさは,35×36×315 μm3とした.また,トレーサには粒径1 μmのオイルミストを用いた.図2に円管の一部を切り取ったサンプルを示す.計測の際,円管表面にテープを貼り平滑性を向上させることで,レーザ光の散乱を防ぎ,透過性を担保した.
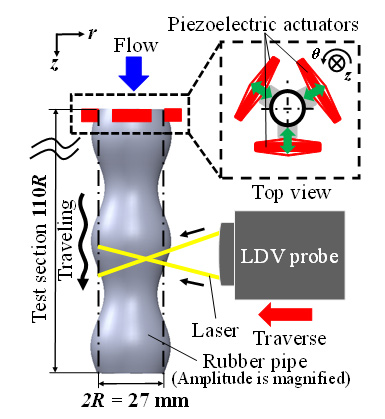
Fig. 1 Schematic of experimental devices.

Fig.2 Sample of rubber pipe.
4. 進行波パラメータ
進行波パラメータは両振幅2η+,波長λ+,位相速度c/uc, lamの3つである.ここで,( )+はReτ = 160で流れを駆動したと仮定した場合の非制御時の摩擦速度uτ [m/s]と動粘性係数ν [m2/s]により無次元化された値を表す.また,uc, lam [m/s]は層流時の中心流速である.図3に進行波パラメータの流れ方向分布を示す.横軸は振動源からの距離を表す.オレンジ色の領域はDNS(2)によって明らかにされた再層流化を示す範囲である.また,図3(c)のc/uc, lam < 0.35の青色の領域は,同結果より抵抗増大が示された範囲である.図3(a)に示すように,振幅は振動の減衰に伴い進行方向に向けて減少したが,円管上流部において再層流化が期待される値を示した.図3(b)に示す波長はおよそ全領域で再層流化が期待される値を示した.一方,図3(c)に示す位相速度は全領域で再層流化域より低いものの,抵抗増大範囲より大きい値を示し,一定の抵抗低減効果が期待される結果となった.
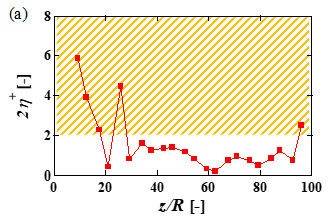
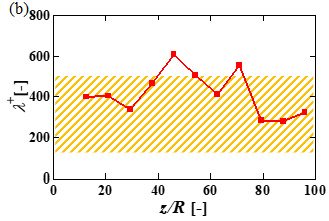
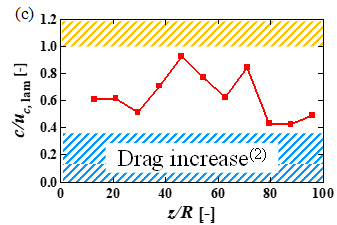
Fig. 3 Streamwise distributions of traveling wave parameters;
(a) wall deformation amplitude, (b) wavelength, (c) wave speed.
5.抵抗低減率
進行波制御による抵抗低減効果を評価するため,差圧計測の結果から式(1)に示す抵抗低減率RD [%]を算出した.ここで,CT, controlとCT, uncontrolは差圧計測から算出された制御時と非制御時の全抵抗係数を表す.図4に抵抗低減率RDのレイノルズ数依存性を示す.青点線の枠内が乱流域を表す.3つの進行波パラメータが抵抗低減に効果的な値を示した乱流域であるReτ = 160に相当するReb = 4800において抵抗低減率 は4.5%であった.
 |
(1) |
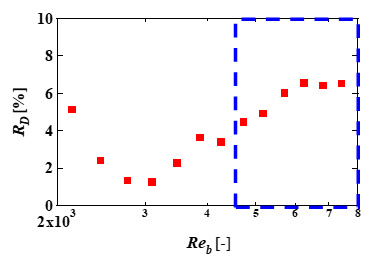
Fig. 4 Dependence of drag reduction rate on bulk Reynolds number.
6.LDV計測
図5にLDV計測から得られたReτ = 160における主流方向の時間平均した流速の壁垂直方向分布をそれぞれ示す.非制御時の平均速度分布は,非制御時のDNS(5)の結果と良い一致を示した.制御時の平均流速において,壁面 (R+ - r+ = 0)で 平均流速が0になることを仮定すると,非制御時と比較して壁近傍における速度勾配が緩やかになると考えられる.これは,速度勾配に比例する壁面せん断応力の減少を表し,摩擦抵抗の低減を意味する.一方で,管中心付近では非制御時と有意な差は確認できず,制御の影響は壁面近傍にのみ生じていると考える.
図6に速度変動のrms値の壁垂直方向分布を示す.制御時には壁面近傍において非制御時と比較して大きな変動を示した.制御が流れ場に与える影響を詳細に評価するため,流速の三成分分解を行った.瞬時の流速は平均成分と変動成分の和で表される.変動成分は周期成分とランダム成分に分解される.ここで,周期成分は進行波制御由来の成分であり,ランダム成分は乱流由来の成分である.緑のプロットで示した周期成分は,壁面近傍で大きな値を示した.一方,青のプロットで示したランダム成分は,壁面近傍で非制御時と比較して小さな値を示した.したがって,制御により壁面近傍の流れ場が変化し,抵抗低減効果が得られたと考えられる.
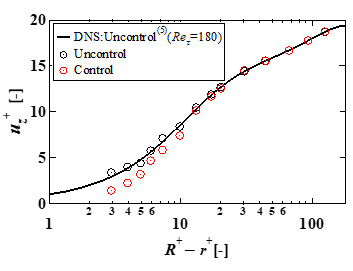
Fig. 5 Time-averaged streamwise velocity profiles.
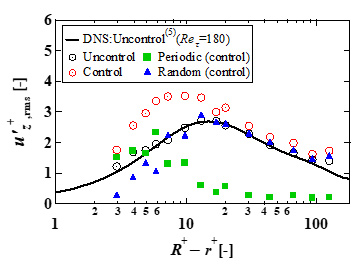
Fig. 6 Profiles of rms value of streamwise velocity fluctuations.
7.結言
円管内乱流において進行波制御による抵抗低減効果を実験的に調査した結果,以下の知見を得た.
| (1) | 進行波パラメータが抵抗低減に効果的な値を示した条件において差圧計測を行った結果,4.5%の抵抗低減を確認した. |
| (2) | 抵抗低減を確認した流れ場においてLDV計測を行った結果,主流方向の平均速度は壁面近傍で減少し,壁面せん断応力の減少が確認された. |
| (3) | 速度変動のrms値の三成分分解の結果,壁面近傍において周期成分が大きな値を示し,非制御時と比較してランダム成分が減少した. |


