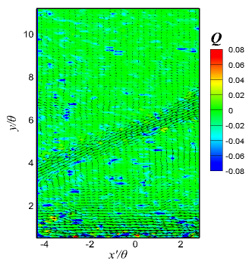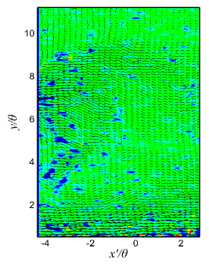
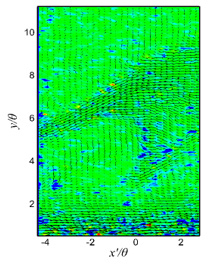
流れ　2020年3月号　目次

―　特集テーマ：流体工学部門講演会　３月号　― 巻頭言 （橋本，松田，朴） 鉄道と風洞実験 井門 敦志（鉄道総合技術研究所） 進行波状弾性壁面を有する円管内乱流の抵抗低減効果 中澤　誠也，志村　敬彬，光石　暁彦，岩本　薫，村田　章（東京農工大学） 弾性運動翼壁面上の渦度の成長過程 刀根 千玖沙，渕脇 正樹（九州工業大学） ステレオPIV計測による抵抗低減乱流境界層流れの大規模乱れ構造の同定法の検討 平野 真琴，玉野 真司，山田 格，森西 洋平（名古屋工業大学）   新しい飲み物 濱田 健吾（明星大学） 　｜　リンク一覧にもどる　｜

 

ステレオPIV計測による抵抗低減乱流境界層流れの大規模乱れ構造の同定法の検討

平野 真琴， 玉野 真司， 山田 格， 森西 洋平 名古屋工業大学

1．はじめに

　日本機械学会第97期流体工学部門講演会において，光栄にも優秀講演表彰を頂くとともに，ニュースレターにて研究内容を紹介する機会を頂いた．この場をお借りして，選考委員間ならびに日本機械学会の皆さまに御礼申し上げる．本ニュースレターでは，私の研究内容である，ステレオPIVによる抵抗低減乱流境界層流れの実験結果およびそれに同定法を適用した結果を示す．

2．概要

　近年，環境問題や化石燃料の枯渇問題の観点から，流体工学において流体輸送の高効率化が求められている．その手法の一つとして，溶媒中に界面活性剤を注入することで，流体との間に生じる流動抵抗を低減させる方法がある．著者らは，抵抗低減乱流境界層流れのPIV計測を行い，乱流統計量分布や瞬時変動速度場を調べることで，抵抗低減メカニズムの解明を進めている⁽¹⁾．また，ごく最近，複数台のカメラを配置し，広範囲にわたる大規模な流れ場の様子を捉えることで，壁面近くの小さな渦構造が抑制されること，流れ構造が主流方向に引き伸ばされ大型化し，それが間欠的に現れることを明らかにしている⁽²⁾．しかしながら，従来のPIV計測では，平面内の速度2成分の情報のみが得られ，速度3成分すべてのデータを用いた解析を行うことができず，大規模流れ構造の詳細ならびにその発生メカニズムの解明には至っていない．

　本研究では，3次元的に流れ構造を捉えるために，2台のカメラを用いて同領域での流れ断面を撮影し，速度3成分をすべて測定可能なステレオPIV計測を実施する．また，流れの様子を捉える上で，流動中の渦の同定やその特徴を把握することは非常に重要である．これまでに様々な渦の同定法^(3)-(5)が提案されているが，本研究ではそれらの中で，速度勾配テンソルの第二不変量および固有値の虚部を用いた渦の同定法に着目し，これらにより大規模な乱れ構造が同定可能かどうかを検討する．

2.1.　実験装置
　本実験で使用する実験装置の概略図を図1に示す．装置は回流水槽であり，400 mm × 400 mm × 3000 mmのアクリル製閉水路測定部（テストセクション）を持つ．遠心式ポンプ（200IFWM2015，荏原製作所（株）製）をインバータ（FR-A720-11K，三菱電機（株）製）で周波数制御することにより作動流体の流速を設定する．また装置内の作動流体は循環式冷水器（RKL-5500-D，オリオン機械（株）製）により水温がほぼ一定（±0.3 ℃）に保たれる．テストセクションには底面に対して垂直に全長2796 mm，幅387 mm，厚さ20 mmのアクリル製テスト プレート（図2）が設置されている．作動流体は整流格子を通過することで一様化される．測定部内の座標は，テストプレート前縁からの流れ方向距離をx，テストプレート壁面からの垂直方向距離をy，後述の注入スロットのスパン方向中心からの距離をzとする．界面活性剤水溶液はテストプレート内に設けられたスロットより注入される．注入口の大きさは，主流方向に1.0 mm，スパン方向に200 mmであり，注入口の流路幅は0.5 mmである．注入口位置はx = 400 mmであり，流れ方向に対して壁面垂直方向に30°傾けられている．

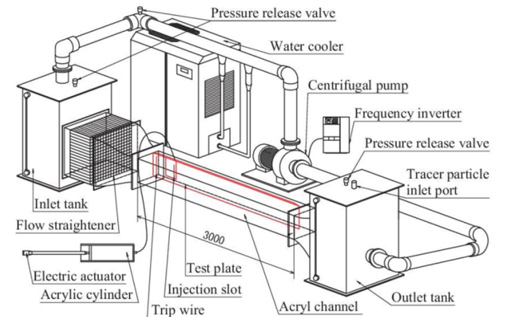
Figure 1　 Schematic of experimental equipment

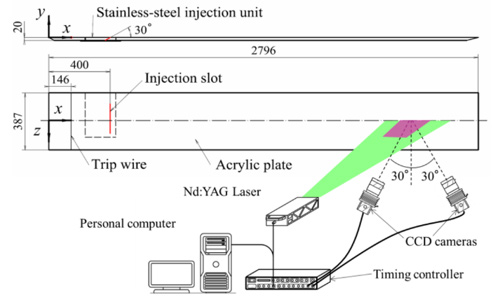
Figure 2　 Test plate and stereoscopic PIV measurement system

2.2　渦構造の同定法
　まず，流れの中の対象とする点を原点と定め，座標系xi（i = 1, 2, 3）とおく．ある点x_iにおける速度v_iの速度勾配テンソルAは以下のように表される．

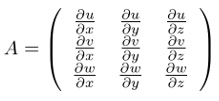（1）

速度勾配テンソルAの固有値をλとすると速度勾配テンソルAの固有方程式は

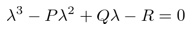（2）

と表すことができる．また，この方程式における固有値は虚数解が存在するため，λ=λ_cr±iλ_ciと表せる．このとき虚数部λ_ciの大きさが流れの旋回強さに相当することが知られている⁽³⁾．また，式（2）における第二不変量Qは流れにおける渦運動が支配的であるとき，正の値をとる．ここで，ステレオPIV計測では測定点がスパン方向に1点だけのため，スパン方向の微分が求められない．したがって，∂u₃/∂x₃は連続の式より算出した．また，∂u₁/∂x₃, ∂u₂/∂x₃はゼロと仮定した．これらを踏まえた速度勾配テンソルは以下で表される．

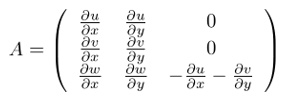（3）

本研究では，式（3）を用いて式（2）の固有方程式の解および第二不変量Qを算出した．

3.　乱流統計平均量によるステレオPIV計測の信頼性確認

　図3に，x = 2400 mmでの界面活性剤水溶液を注入した流れ場のステレオPIV計測により得られた各種乱流統計量を示す．ここで，x = 2400 mmにおける抵抗低減率DRは70%である．図3（a）には平均速度U/U_e，図3（b）には主流方向乱流強度u'_rms/U_e，図3（c）には壁面垂直方向乱流強度v'_rms/U_e，図3（d）にはスパン方向乱流強度w'_rms/U_eの分布をそれぞれ示す．また，図3（a）～（c）には，ステレオPIV計測結果の信頼性確認のため，通常のPIV計測結果も示されている．図3（d）には，Silleroら⁽⁶⁾のDNSの結果（図3（d）中の破線）と比較するため，水流の結果も示されている．平均速度分布（図3（a））および主流方向乱流強度分布（図3（b））を見ると，ステレオPIV計測結果は通常のPIV計測結果に近いことが分かる．一方，壁面垂直方向およびスパン方向の乱流強度分布は境界層内全体の分布形状に問題はないものの，壁面近傍でゼロに漸近しておらず（図3（c）および（d）），壁面近傍の測定精度が十分とは言えない．これより，本ステレオPIV計測により，壁面ごく近傍を除き，瞬時の乱流構造を考察できると判断した．

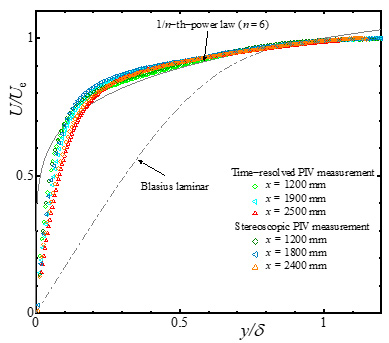
（a）Mean velocity

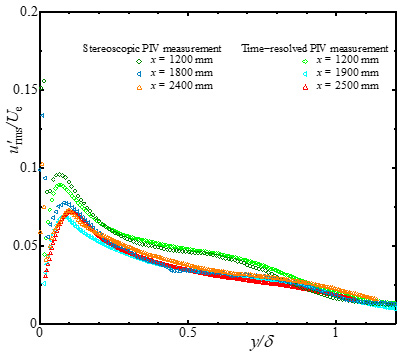
（b）Streamwise turbulence intensity

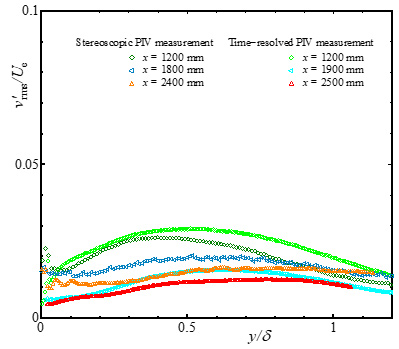
（c）Wall-normal turbulence intensity

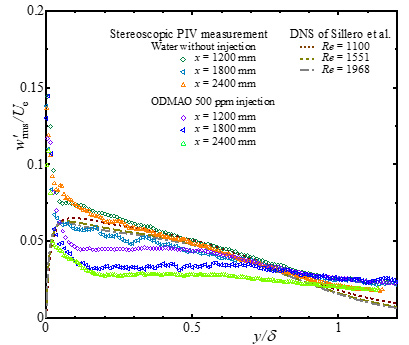
（d）Spanwise turbulence intensity
Figure 3　 Profiles of mean velocity and turbulence intensities with outer scaling in drag-reducing flow

4．瞬時変動速度ベクトル場

　図4および図5に，x = 2400 mm（x’ = 0 mm）での界面活性剤水溶液を注入した流れ場における流れ方向と壁面垂直方向 x-y 断面での変動速度ベクトル (u’, v’) に，速度勾配テンソルの第二不変量Qのコンターおよび固有値の虚数部λ_ciのコンターを重ねた瞬時場を示す．これらの図には，ある時刻t₀から0.1 s間隔の連続した3時刻における結果がそれぞれ図4，5（a）～（c）に示されている．縦軸は壁面垂直方向距離yであり，横軸x'は測定領域中心からの主流方向距離であり，x'=0mmがx=2400mmに対応する．これらは共に運動量厚さθで正規化されている．また，第二不変量Qおよび固有値の虚部|λ_ci|は運動量厚さθ，主流方向速度Ueで正規化されている．

　図4における第二不変量Qのコンターと変動速度ベクトルから判別できる大規模な乱れ構造の対応関係を見ると，Q値の大きなコンターが乱れ構造の近くに密集しているが，大規模な乱れ構造との対応関係は見られない．

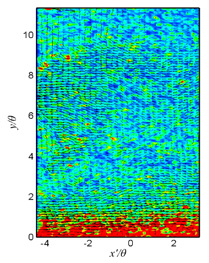
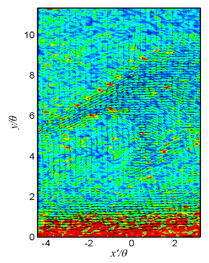
　図5における固有値の虚部|λ_ci|では，変動速度ベクトルから判別できる大規模な乱れ構造の周辺には値の大きなコンターが密集している様子が確認できる．しかし，乱れ構造が確認できない他の領域でも値の大きなコンターが点在しており，大規模な乱れ構造を同定できているとまでは言えない．

(a) t=t0+0s	(b) t=t0+0.1s	(c) t=t0+0.2s
Figure 4　 Contours of second invariant of velocity gradient tensor and fluctuation velocity vectors on x-y plane in active state of drag-reducing flow at x=2400mm

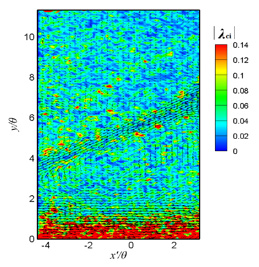(a) t=t0+0s	(b) t=t0+0.1s	(c) t=t0+0.2s
Figure 5　 Contours of magnitude of imaginary part of eigenvalue and fluctuation velocity vectors on x-y plan in drag-reducing flow at x=2400mm

5.　結　　　言

　抵抗低減乱流境界層流れのステレオPIV計測による乱流統計平均量の分布より，壁面近傍を除き，測定の信頼性が確認された．ステレオPIV計測により得られた瞬時の速度成分データを用い，速度勾配テンソルの第二不変量および固有値の虚部に基づく渦の同定法により，大規模な乱れ構造の同定の可能性を検討した．その結果，これらの渦同定法では，変動速度ベクトルから判別できる大規模乱れ構造との明確な対応関係が見られないことが明らかになった．そのため，大規模乱れ構造は強い旋回を伴わない構造であると言える．

6. 謝　　　辞

　本研究は，科学研究費補助金（JPI5H03918）の補助を受けています．また，ライオン・スペシャリティ・ケミカルズ（株）より界面活性剤（カデナックス）の提供を受けました．ここに記して感謝の意を表します．また，末筆となりますが，ご指導頂きました名古屋工業大学　玉野真司准教授ならびに当日会場にて貴重なご質問を頂きました皆様に深く感謝申し上げます．

文　　　献

(1)	Tamano S., Kitano T., and Morinishi Y., Experimental study on drag-reducing turbulent boundary layer with nonionic surfactant injection from wall surface, J. Fluid Mech., Vol. 749, 367-403．
(2)	Tamano S., Katsuragawa S., Yamamoto D., Yamada T., and Morinishi Y., Experimental study on large-scale turbulence structures in drag-reducing turbulent boundary layer flow, Proc. The Ninth JSME-KSME Thermal and Fluids Eng. Conf., Okinawa, Japan, 28-30 October, (2017).
(3)	Li, F. C., Kawaguchi, Y., Hishida, K., and Oshima, M., Investigation of turbulence structures in a drag-reduced turbulent channel flow with surfactant additive by stereoscopic particle image velocimetry, Exp. Fluids, Vol. 40 (2006), pp. 221-222．
(4)	Hunt, J. C. R., Wray, A. A., and Moin, P., Eddies, streams, and convergence zones in turbulent flows, Center for Turbulence Research, CTR-S88, (1988), pp. 193-208.
(5)	Jeong, J. and Hussain, F., On the identification of a vortex,J. Fluid Mech., Vol. 285, (1995), pp. 69-94.
(6)	Sillero, J. A., Jimenez, J., and Moser, R. D., Two-point statistics for turbulent boundary layers and channels at Reynolds numbers up to δ+ ≈2000, Phys. Fluids, Vol. 26, (2014), 105109.