 |
 |
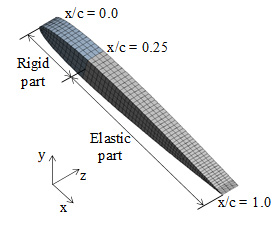
| (a) Structure region | (b) Around the airfoil of fluid region |
| Fig. 1 Numerical mesh of structure and fluid region | |
流れ 2020年3月号 目次
― 特集テーマ:流体工学部門講演会 3月号 ―
| リンク一覧にもどる | |
弾性運動翼壁面上の渦度の成長過程
刀根 千玖沙 |
1. はじめに
令和元年11月7日,8日の2日間にわたり,ホテルアソシア豊橋で開催された日本機械学会 第97期 流体工学部門講演会において,光栄にも優秀講演賞を頂きました.この場をお借りして,選考委員会の皆様および日本機械学会流体工学部門の皆様に御礼を申し上げるとともに講演発表内容を以下に紹介させて頂きます.
2. 背景および目的
代表的非定常流れの一つである運動翼まわりの流れ場は,渦流れに関わる基礎現象として注目されており,古くから研究されている.近年では,剛体翼に限らず,弾性翼,さらには,弾性薄膜を対象とした運動体まわりの流れ場に関する研究が盛んに行われ,その流れ場だけでなくその非定常流体力特性も明らかにされている(1) - (3). 著者らも,これまでに,非定常運動する剛体翼および弾性翼まわりの渦構造,さらには,その非定常流体力特性を実験計測および数値シミュレーションにより行ってきた(4)(5).その中で,弾性運動翼は,剛体運動翼に比べて,強い渦度を持つ渦を翼後流に巻き上げ,その結果,大きな推進力を生みだすことも明らかにしている.すなわち,弾性翼と剛体翼では,翼後流に巻き上がる渦の特性が異なると言える.弾性翼は,その運動により弾性変形することが最大の特徴であり,弾性運動体まわりの流れ場は流体構造連成問題として取り上げられるなど,近年注目されている流れ場の一つである.しかしながら,弾性変形といえども,瞬間的に見ると単純な壁面の移動である.本研究では,この瞬間的な壁面の移動こそが弾性翼から巻き上がる渦の特性,さらには,後流に巻き上がる渦を作り出す壁面近傍の渦度の成長に寄与していると予想した.そのため,本研究では,弾性変形を瞬間的な壁面の移動として評価するために,壁面の空間勾配を定義し,その空間勾配に対する渦度の成長を捉え,弾性変形が渦度の成長に与える効果を明らかにした.異なる弾性変形を行う3種の運動翼まわりの流れ場をANSYS 17.0 / ANSYS CFX 17.0を用いた流体構造連成解析により定性的/定量的に可視化し,さらには,その可視化結果と壁面近傍の渦度を関連付けることで,壁面の空間勾配が壁面を成長する渦度に与える効果を明らかにする.
3. 解析モデルおよび解析条件
本研究の流体構造連成解析に用いた試翼はNACA0010,NACA0020および平板である.NACA0010の構造領域と流体領域の解析モデルをそれぞれ図1(a)および(b)に示す.構造領域は,翼弦長cに対して前縁から25%が剛体部,それ以降が弾性部となる.
構造領域の計算格子はそれぞれ約5,000,17,000および10,500,流体領域の計算格子はそれぞれ約280,000,150,000および272,900である.また,NACA0010,NACA0020および平板の弾性変形による後縁の最大変位を揃えるために,ヤング率はそれぞれ0.06 MPa,0.015 MPaおよび0.24 MPaとした.弾性翼の弾性変形は非線形性が強く,ばねの計算などに用いるフックの法則を適用することができないため,Neo-Hookeanモデルを使用した.構造解析の支配方程式は多自由度減衰系の運動方程式であり,流体解析の支配方程式は連続の式とNavier-Stokes方程式である.翼の基本迎え角は定常状態ではく離を生じる迎え角α = 16˚であり,式(1)に示すヒービング運動を与え,その最大振幅はA = 0.2cとした.St数は式(2)により定義し,St = 0.3とした.
| y = Asin(2πft) | (1) |
| St = 2Af / V0 | (2) |
乱流モデルはRANSを用い,翼面上の流れを捉えることを目的とするため,壁面近傍の挙動をモデル化しやすく,格子依存性が小さいk-ωを使用した.本研究の流体構造連成解析は弱連成の双方向解析を行っている.双方向解析では,流体解析により得られた翼面にかかる圧力を構造領域へ受け渡し,受け渡された圧力をもとに構造解析により構造の変形量を求め,構造の変位を流体領域へ受け渡すというように,流体領域と構造領域で圧力や変位のやり取りをしている.このやり取りを複数回重ね,解析を繰り返すことで,最終的に弾性運動翼まわりの流れ場を明らかにする.
本研究では,弾性翼を瞬間的な壁面の移動として注目した.すなわち,図2に示すように,弾性翼は,その弾性変形により,翼弦方向の位置によってその瞬間の空間勾配dy/dxが異なる.特に,その弾性変形は,翼後縁に近づくにつれて大きくなるために,空間勾配も大きくなる.また,ヒービング運動に伴い弾性変形量も変化するため,時間に対しても空間勾配が変化する.本研究では,空間勾配の大きさではなく,空間勾配の時間変化d(dy/dx)/dtが大きいことが渦度の発達に大きな影響を与えていると考える.そのため,本研究では,空間勾配の時間変化に対する渦度の発展に注目した.特に,弾性変形が大きくなる弾性翼が下向きに変形する時の空間勾配の時間変化に対する渦度の発展に注目した.
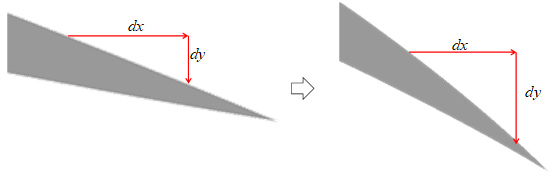
Fig. 2 Spatial gradient of wall of a moving elastic airfoil
4. 結果および考察
4・1 弾性翼壁面の空間勾配の時間変化
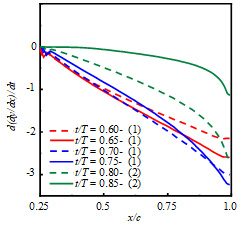
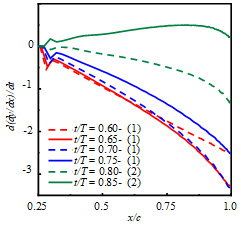
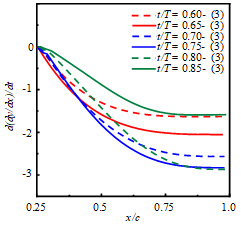
ヒービング運動するNACA0010,NACA0020および平板の壁面の空間勾配の時間変化をそれぞれ図3(a),(b)および(c)に示す.横軸および縦軸にそれぞれ弾性部の位置および空間勾配の時間変化を示す.縦軸の値が負を示すと,その弾性変形は直前の時刻より下向きに変形し,正を示すと,直前の時刻より上向きに変形することを意味する.
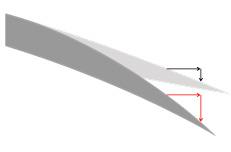
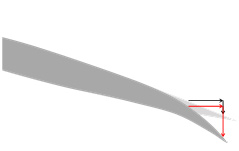
これらの結果より,壁面の空間勾配の時間変化は,3つに分けることができる.まず,翼弦方向に対して線形的に変化する(NACA0010,NACA0020:t/T = 0.60 – 0.80,図(1)).次に,後縁近傍まではほぼ一定となり,後縁だけ負側へ大きくなる(NACA0010,NACA0020:t/T = 0.80 – 0.90,図(2)).最後に,後縁近傍までは線形的に変化し,後縁だけ一定となる(平板:t/T = 0.60 – 0.90,図(3)).これらは,それぞれ図4(a),(b)および(c)に示すような弾性変形となる.すなわち,図4(a)のように,後縁に進むにつれて大きくなる弾性変形,図4(b)のように,後縁近傍のみ大きな弾性変形,図4(c)のように,後縁近傍はほぼ同等に弾性変形を行う.
 |
 |
 |
| (a) NACA0010 | (b) NACA0020 | (c) Flat plate |
| Fig. 3 Temporal change of spatial gradient of the wall in elastic part | ||
 |
 |
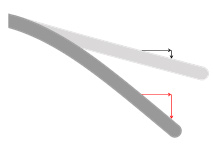 |
| (a) Deforming almost linearly | (b) Deforming only trailing edge | (c) Deforming of trailing edge constantly |
| Fig. 4 Three kinds of elastic deformation of the elastic part | ||
4・2 弾性翼後縁近傍の渦度分布
ヒービング運動するNACA0010,NACA0020および平板の無次元周期t/T = 0.65,0.75および0.85における後縁近傍の等渦度線図をそれぞれ図5(a),(b)および(c)に示す.等渦度線図は全て時計回転の渦度を表している.いずれの結果からも,翼面上の渦度が確認でき,時間の経過と共に,これらは翼後縁側へと移動することがわかる.さらには,後縁側へ進むにつれ,後縁まで拡がった渦度は,後縁近傍において厚みを増していることもわかる.これらの可視化結果より,壁面近傍の渦度の成長は定性的には理解できるが,その詳細までは理解できない.
そのため,壁面近傍の渦度を定量的に評価した.

(a) t/T = 0.65

(b) t/T = 0.75
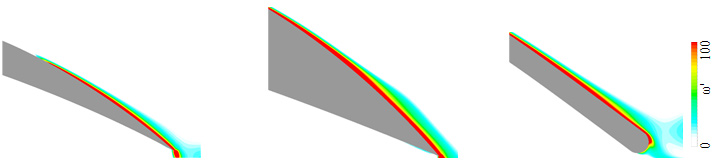
(c) t/T = 0.85
Fig. 5 Vorticity contour in vicinity of wall of three kinds of airfoils, NACA0010,NACA0020 and flat plate
4・3 弾性翼壁面近傍を成長する渦度
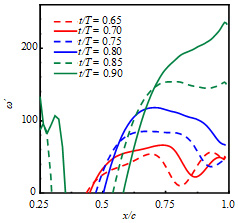
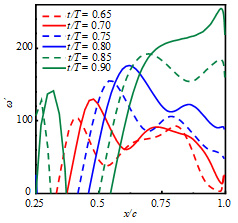
ヒービング運動するNACA0010,NACA0020および平板の無次元渦度(第二格子点の渦度を無次元化)をそれぞれ図6(a),(b)および(c)に示す.横軸および縦軸は,それぞれ弾性部の位置および無次元渦度を示す.
図6(a)および(b)に示したNACA0010およびNACA0020では,x/c = 0.75付近にある渦度のピークが時間の経過と共に,次第に大きくなりながら,後縁側へ移動している.t/T = 0.85 – 0.90では,渦度のピークが後縁まで移動し,その後は,その場で大きくなる.図6(c)の平板では,t/T = 0.60 – 0.90においては,NACA0010およびNACA0020と同様に,x/c = 0.75付近の渦度のピークは大きくなるが,後縁側へ移動していない.
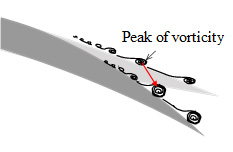
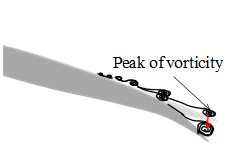
これらの結果を図4に示した壁面の空間勾配の時間変化と関連付け,空間勾配の時間変化に対する渦度の成長の模式図をそれぞれ図7(a),(b)および(c)に示す.図4に示したように,壁面の空間勾配の時間変化は3つに分けられた.いずれにおいても,壁面上の渦度分布は時間の経過と共に後縁側へ広くなることが,図5だけでなく,図6からも定量的に理解できた.しかしながら,その渦度のピークの挙動に注目すると,図6に示したように,NACA0010およびNACA0020はそのピークが発達しながら後縁側へ移動し,平板は,そのピークは発達するものの,ほとんど後縁側へ移動していない.これらの結果より,壁面の空間勾配の時間変化が線形的に変化する時,すなわち,弾性変形が後縁に進むにつれて大きくなる時に,渦度は成長するだけでなく,後縁側へ移流するが,後縁近傍の空間勾配の時間変化がほぼ一定となる時,すなわち,弾性変形は大きくても後縁近傍がほぼ同じ割合で変形している時には,渦度は成長こそするものの,その後縁側への移流は小さくなると言える.
 |
 |
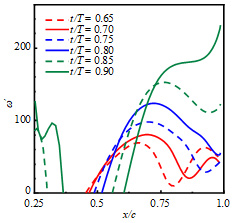 |
| (a) NACA0010 | (b) NACA0020 | (c) Flat plate |
| Fig. 6 Non-dimensional vorticities in the vicinity of the wall of three kinds of airfoils, NACA0010, NACA0020 and flat plate | ||
 |
 |
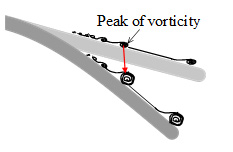 |
| (a) Deforming almost linearly | (b) Deforming only trailing edge | (c) Deforming of trailing edge constantly |
| Fig. 7 Pattern diagrams of growth of vorticities on the wall of three kinds of elastic deformation | ||
5. 結 言
弾性運動翼の弾性変形が瞬間的な壁面の移動であることに注目し,流体構造連成解析を用いて,壁面の空間勾配の時間変化とその渦度の成長について考察した.壁面の空間勾配の時間変化が線形的に変化する時,すなわち,弾性変形が後縁に進むにつれて大きくなる時に,壁面近傍の渦度は成長するだけでなく,後縁側へ移流する.その一方,後縁近傍の空間勾配の時間変化がほぼ一定となる時,すなわち,弾性変形は大きくても後縁近傍がほぼ同じ割合で変形している時には,渦度は成長こそするものの,その後縁側への移流は小さくなる.



