流れ 2021年4月号 目次
― 特集テーマ:流体工学部門講演会 4月号 ―
| リンク一覧にもどる | |
液晶の背流とマイクロアクチュエータの開発
|
本稿は,2020年度日本機械学会 第98期流体工学部門講演会(2020年11月11日~13日,オンライン)における筆者らの基調講演を要約したものである.流体工学部門ニュースレターへ掲載する機会を頂いたことに対し,関係各位に心から感謝申し上げる.
1.はじめに
一般に,ある集団に何らかの規則性があると,私たちは“秩序がある”と言う.分子形状が球状の物質の場合,分子の重心位置が秩序の有無の対象となるが,分子形状が棒状の物質では,分子の重心位置に加えて分子の方向(配向)も秩序の有無の対象となる.位置と配向の両者ともに秩序がある状態を固体,両者ともに無秩序の状態を液体,そして配向の秩序はあるが位置については無秩序の状態を液晶と呼ぶ.位置について無秩序とは大変形が可能ということで,より卑近な表現をすれば“流れる”ということである.
すなわち液晶は,分子の配向に関して異方性を有しながら通常の液体のように流動するユニークな物質,または状態である.本稿では,低分子ネマティック液晶に限定して,液晶の流動について概説した後,分子の回転が誘起する流動(背流と呼ばれる)を利用したアクチュエータの開発を目指した研究を紹介する.
2.液晶の流動
電場下にある液晶の等温流れを記述する基礎式は以下である.
| ・連続の式 | |
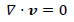 |
(1) |
| ・運動方程式 | |
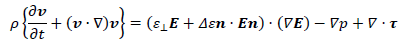 |
(2) |
| ・構成方程式(Leslie-Ericksen理論(1)~(3)) | |
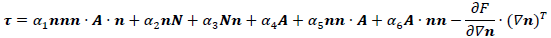 |
(3) |
| ・角運動方程式 | |
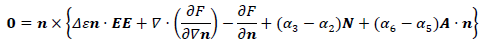 |
(4) |
| ・ディレクタの弾性ひずみに基づくFrankの自由エネルギー密度 | |
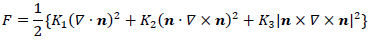 |
(5) |
| ・ディレクタの相対角速度ベクトル | |
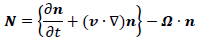 |
(6) |
ここで,vは速度ベクトル,ρは液晶の密度,pは圧力,τは偏差応力テンソル,nは液晶分子の局所的平均配向方向を表す単位ベクトルでディレクタ,α1~α6はレズリー粘性係数,K1~K3は分子場弾性定数,Eは電場ベクトル,ε⊥およびε//はそれぞれディレクタに垂直および平行方向の誘電率,Δε=ε//-ε⊥は誘電率の異方性,Aは変形速度テンソル,Ωは渦度テンソルである.なお,式(2)の右辺第1項は電場による単位体積当たりの外力,式(4)の右辺第1項は電場によるディレクタに作用する単位体積当たりの外トルクである.通常の等方性流体では速度場vと圧力場 p が未知量であるが,液晶の場合はさらに配向場 n が未知量であるので,それを規定するためにディレクタの角運動方程式(4)が必要となる.
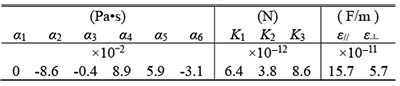
本研究の実験と数値計算で用いた液晶は,4-cyano-4’-pentyl biphenyl (5CB)である.この液晶は22.5~35°Cの温度範囲で液晶相を発現する.5CBの物性値を表1に示す(4)~(6).なお,密度は1000 kg/m3とした.
Table 1 Material constants of 5CB
3.マイクロアクチュエータの開発
一般に,せん断流や伸長流のような速度勾配が存在すると,棒状の液晶分子はトルクを受けて回転して別の方向に再配向することは周知の事実である.例えば,縮小部近傍では主流方向に配向するし,拡大部直後では主流に対して垂直に配向する.それではこれと逆の現象,すなわち“液晶分子が回転して別の方向に再配向したとき,そこに速度勾配が誘起される”という現象は成立するのかという疑問を発想した.液晶分子の回転は,例えば外部から電場を印加すればよい.式(2)や式(4)から,配向場nが変化すれば速度場vも変化することは容易に推測できるので,理屈上は成立するはずである.もしそうなら,液晶を介して電気エネルギーを運動エネルギーに変換することになり,液晶の用途が拡大するだけでなく新規な機械要素開発にも繋がる.
詳細は文献(7)を参照して頂きたいが,電場を印加すると流動が発生することを数値計算と可視化実験で確認するとともに,壁面での分子配向を工夫すれば固定された2平板間に様々な速度分布が誘起されることを見出した.なお,この流動は“背流(back flow)”という名称で過去に論じられているが(8)(9),それらの研究は背流が分子挙動に及ぼす影響を調べることであり,力学的応用を目指したものではない.
3.1 平板アクチュエータ
固定された2平板のうち上部平板を平面方向に可動な状態にすれば,平板に作用するせん断力で上部平板が駆動される.これが液晶アクチュエータの駆動原理である.ただし,液晶分子の回転が背流を誘起するのであるから,電場印加状態を保持したままなら新たな背流は発生せず,むしろ粘性のために最初の背流は短時間で消失する.そのため上部平板を連続駆動させるには,電場を一旦解放し分子を元の配向状態に戻して再印加するという操作が必要である.従って,電圧値V(正確にはVを平板間隔Hで除した電場強度E)以外に印加周波数fとデューティー比Dという物理量が液晶アクチュエータの性能を決定することになる.なお,電場解放時,液晶分子は逆回転するので上部平板は後退し,印加時の前進と相殺するのではという疑問が生じる.確かに解放時,上部平板は後退するが,電場印加時の分子の強制回転が誘起すると前進量に比べれば後退量は極めて小さく,正味として上部平板は前進する.
数値解析のモデル化について簡潔に述べる.平板駆動の概略を図1に示す.厳密には平板端面の影響を考慮した3次元モデルを提案すべきであるが,平板間隔に比して平板は十分広いので,端面の影響は無視できると考え,近似的に平板間隔方向の1次元のモデル化を行った.一方,上部平板の運動方程式は以下となる.
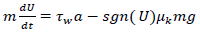 |
(7) |
ここで,mとUはそれぞれ上部平板の質量と速度,τwは上部平板に作用する液晶の流れ方向せん断応力,aは液晶と上部平板との接触面積,μkは2平板の間隔を一定に保持するために液晶中に分散した微粒子と上部平板との動摩擦係数である.式(1)~式(6)の液晶流動と式(7)の平板運動を連成して数値計算を行った.
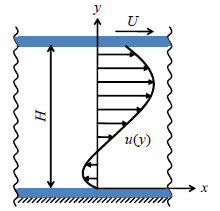
Fig. 1 Coordinate of a liquid crystal actuator
実験結果と計算結果を併記して図2に示す.実験では10個の異なったセルに対して測定を行い,その平均値をエラーバーとともにプロットしている.f の増加とともに U は急増し,f=175 Hzにおいて最大値約120 μm/sを取った後,緩やかな減少に転じている.f が小さい場合,液晶分子の回転運動は周期に追従できるので,fの増加は単位時間あたりの繰り返し数の増加になり,結果としてUは増加する.しかし,fが大きくなると分子はこれに追従できなくなり,分子の回転運動が満足な背流を誘起できないので繰り返し数の増加に反してUは減少したと推察される.なお,実験については文献(10)を,数値計算については文献(11)を参照して頂きたい.
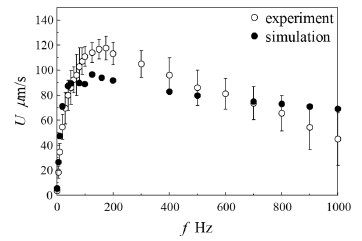
Fig. 2 Dependence of the speed of the upper plate on frequency of the applied voltage when V=10 V, D=5 %, and H=10 μm. The speed exhibits a sharp increase, attains a maximum value of 120 μm/s at f=175 Hz, and then decreases gradually with increasing f.
3.2 モータ
液晶は巨視的には通常の液体のように振る舞うことから,充填するケーシングが平板である必要はなく,曲板でもよいし円筒でも形状適合する.そこで同心2重円筒を用意し,その間隙に液晶を充填して,背流が周方向に発生するように壁面配向を工夫すれば,2つの円筒は相対的に回転するので,外筒を固定し内筒をフリーにすればモータとなる.図3は外筒の外径が0.2mm,内筒の外径が0.1mm,ギャップが5μmの液晶モータである.図4は,印加電圧V=10V,周波数f=500Hz,デューティー比D=5%のとき,最大30rpmで回転した動画である.詳細については文献(12)を参照して頂きたい.
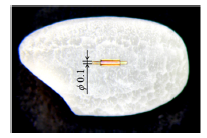
Fig. 3 Microscope image of a liquid crystal motor placed on a grain of rice for a comparison of scale. The outer diameters of the inner and outer cylinders are 0.1mm and 0.2mm, and the gap between two cylinders is 5μm.
Fig. 4 The maximum rotation speed is 30rpm when V=10V, f=500Hz and D=5%.
4.おわりに
液晶は,これまでディスプレイとして光学分野で利用されてきたが,そもそも液晶は固体と液体の中間の状態である.従って,機械工学における「固体力学」や「流体力学」のように,液晶に対して力学的側面からアプローチする研究があっても不思議ではない.液晶を機械工学分野に応用する研究は始まったばかりである.「液晶力学」,「液晶流動工学」に関する広範な研究が期待される.



