流れ　2021年4月号　目次

―　特集テーマ：流体工学部門講演会　4月号　― 巻頭言 （橋本，松田，朴） 液晶の背流とマイクロアクチュエータの開発 蝶野 成臣，辻 知宏（高知工科大学） 非ニュートン性流体の粘弾性は粒子の分散状態に影響されるか？ 芳田 泰基，田坂 裕司，村井 祐一（北海道大学） フローフォーカシングデバイスによるマイクロ液滴生成手法の開発 塩崎 寛子，藤原 裕貴，杵淵 郁也，一柳 満久，田川 義之，高木 周（東京大学） 流れの夢コンテストに参加して 大橋 弘明，逢坂 竜之介，森野 魁人，竹内 文哉（摂南大学） 　｜　リンク一覧にもどる　｜

 

非ニュートン性流体の粘弾性は粒子の分散状態に影響されるか？

芳田 泰基， 田坂 裕司， 村井 祐一 北海道大学

0.　はじめに

　2020年11月オンライン開催となった第98期流体工学部門講演会において，光栄にも優秀講演表彰を頂くとともに，ニュースレターにて研究内容を紹介する機会を頂いた．選考委員会及び日本機械学会の皆様に，この場をお借りして御礼を申し上げる．

1.　緒　　　言

　A. Einsteinは，分散粒子を含む流体における実効粘度を近似式，

(1)

を流体力学的に導いた[1]．ここで，ηは比粘度，μ^*は混相流体における実効粘度，μは分散媒の粘度，φは分散粒子の体積率を示す．このアインシュタインの粘度式による近似には，単純せん断流れや，ストークス近似，十分な分散体の希薄条件（φ < 0.1），完全球形，並びに中性浮力状態など，最低限満たすべき前提条件がいくつかある．現在に至るまで，分散体の形状や高濃度分散など，様々な混相流体の実効粘度を近似するため，式(1)の修正式がいくつも提案されてきた（例えば，[2]）．

Figure 1 A picture taken from the top of cylinder, showing aligned particles in PAM solution under oscillatory flow.

　ここまでの話は，媒質がニュートン性流体の場合に限られる．粘弾性流体では一様には分散せず，粒子がせん断方向へ自ずと配列する（図1）．さらに興味深いことに，このように粒子が配列すると，一様に分散しているときに比べて，流体から加わる正味の抵抗が徐々に減少していくことが知られている[3]．すなわち，粒子の分散状態がせん断に応じて変化し，巨視的な物性変化を引き起こしていることになる．

　本研究では，表題の通り，非ニュートン性流体の実効粘弾性は粒子の分散状態に影響されるかを検証した．そのための計測手段として，超音波スピニングレオメトリ[4−6]を用い，粒子配列現象が与える実効粘弾性変化を定量的に評価した．評価結果に対する考察を基に，トイモデルによる数値シミュレーションを行い，粒子配列を形成するメカニズムについて議論する．

2.　超音波スピニングレオメトリ（USR）

　上部が開放された円筒容器（内径2R = 145 mm，肉厚2.5 mm）を試験対象の流体で満たし，周波数f_o，振幅Θの正弦波で振動させ，内部にせん断流れを生じさせる（図2a）．超音波送受信器を円筒軸中心からO(10 mm)ずらして設置し，発信した超音波パルスによって，内部のエコー情報を計測する．この時，得られたドップラー周波数が，超音波パルスビーム上の瞬時流速分布に相当する．理想的な軸対称性を有する周方向一方向流れが実現されていれば，円筒内部の流動は角運動量保存則から，

(2)

で表せる．ここで，〈u〉，〈τ〉は，円盤状の超音波パルスの単位計測体積（図2b）で計算される，体積平均流速とせん断応力である（以降，u，τと表記する）．USRは，得られた瞬時流速分布を拘束条件として運動方程式に与え，レオロジー物性を逆算的に評価する方法である．本研究では粘弾性を評価するために，せん断応力と流速変動の関係を示す式として，マックスウェルモデル，τ + λ(∂τ/∂t) = μ(∂u/∂r − u/r)を選択した．ω_o(= 2πf_o)は角周波数，λは緩和時間であり，粘性係数μと弾性係数Eからλ = μ/Eで定義する．物性評価の具体的な方法については，先行研究[4,5]を参照していただきたい．

  
Figure 2 Schematics of (a) experimental setup and (b) measurement volume of ultrasonic pulse, and (c) radial profiles of relaxation time λ calculated from the evaluated results.

　USRによって，三種の流体（シリコンオイル 0.97 Pa s，Shin-Etsu Chemical Co. Ltd.; ポリアクリルアミド PAM 0.5 wt.%, MT Aqua Polymer, Inc.; カルボキシメチルセルロース CMC 1.0 wt.%, Daicel Chemical Industries, Ltd.）それぞれの緩和時間を定量評価した（図2c）．三種の流体は，ニュートン粘性，粘弾性，擬塑性を持つ流体としてよく知られており，評価されたλの長短にもそれらの特徴が表れている．弾性的特徴が大きくなるほどλは長くなり，粘性的になるほど短くなる．本実験のように非定常な流動条件ではないが，粒子配列現象に関する先行研究において，λ ≈ O(10⁻² s)が配列形成の臨界値として報告されている[7]．この報告に従えば，円筒内座標において，粘弾性流体（PAM）では全半径領域，擬塑性流体（CMC）ではr/R < 0.75で，粒子が配列を形成することが予想できる．

3.　粒子配列と実効粘弾性

　上記三種の流体密度とほぼ同等な密度を有する，平均粒径O(0.1 − 1 mm)の粒子が体積率φ(= 0 − 0.06)で分散した試験流体を用意した．各混相物質間の密度差による慣性力及び浮力による効果は，媒質となる液体の粘性力に比べて非常に小さいため，計測中に働く円筒半径方向の慣性力や軸方向の浮力対流は無視できる．十分に大きい評価体積を担保するため，各半径Δ(r/R) = 0.05毎に粘弾性を算出した．単相状態における値で規格化し，混相状態の実効粘弾性を円筒内の空間分布として評価した．

　粒子が一様に分散したニュートン性流体を数分間振動させたところ，一様分散状態を維持した（図3a上）．規格化された比粘度η(= μ^*/μ)は，円筒内半径位置において，式(1)で見積もられる比粘度とほぼ同等の値を示した（図3a下）．なお媒質がニュートン流体であるため，弾性は計測されなかった．

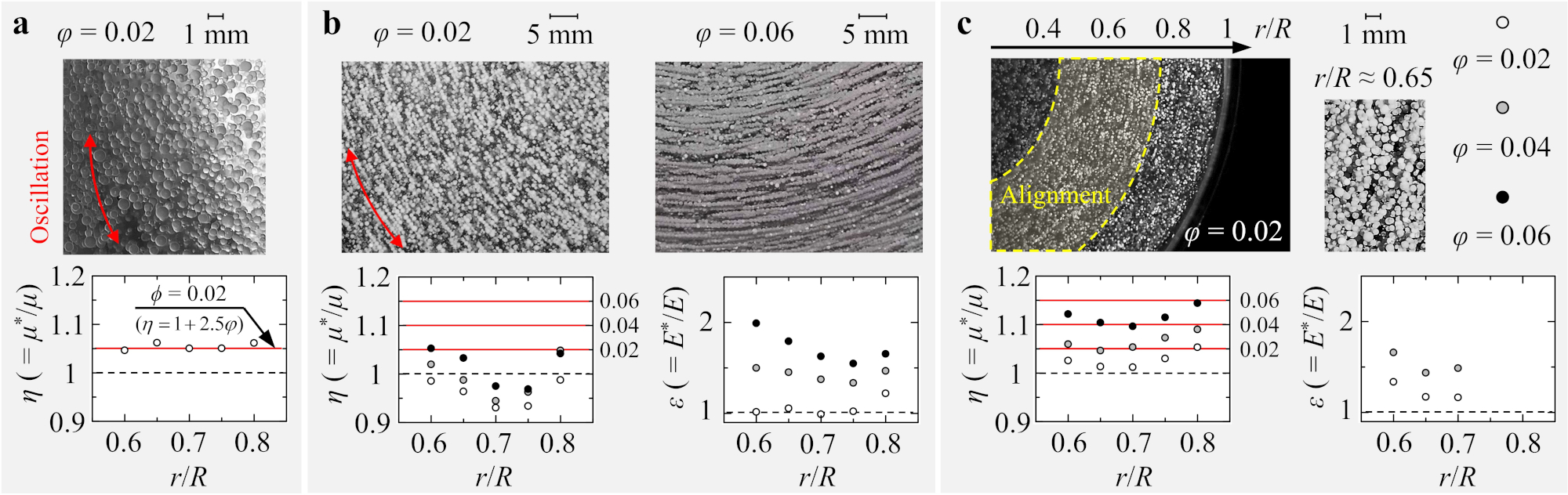
Figure 3 Photograph taken from the top of the cylinder during oscillations, and radial profile of the relative viscosity η and the relative elasticity ϵ, where the solid line indicates the relative viscosity estimated by Eq. (1); (a) silicon oil, (b) PAM solution, and (c) CMC solution.

　一方，粘弾性流体(PAM)では，一様に分散していた粒子がせん断方向に配列を形成した（図3b上）．この写真からもわかるように，粒子の体積率が大きくなるにつれて，配列粒子が長い鎖のような状態となり，円筒内部のほぼ全半径位置で同様の傾向が確認できた．ηを評価した結果，式(1)で見積もられる値より小さくなり，比弾性ε (= E^*/E)は増加傾向を示した（図3b下）．ηに関しては，均一に分散する粒子に比べて，粒子が配列することで伝播する運動量輸送の相対的な減少が指摘できる．εに関しては，配列粒子の度合い（長さ）と比弾性との間にある相関関係が推測できる．

　最後に擬塑性流体（CMC）では，PAMのような鮮明な粒子配列は確認できないものの，図3c上で示した点線内でせん断方向に粒子の配列が確認できた．粒子が一様に分散している壁面近傍の半径位置と単相状態におけるλの半径分布（図2c）を比較すると，配列が形成されている半径位置とλ > O(10⁻² s)の半径位置が一致することが読み取れる．η及びεに着目すると，粒子配列が確認できる半径位置では，ηが式(1)よりやや小さい値を示し，εはやや増加傾向を示した（図3c下）．強調したいのは，一様に分散していた壁面近傍（r/R > 0.75）において，式(1)によって見積もれるηと計測された値がほぼ同じという点である．

　実験結果を要するに，異なるレオロジー的性質を持つ三つの流体では，非定常剪断中の粒子分散状態が変容し，粒子が配列することで実効粘弾性が変化した．それら知見を下記の通り，箇条書きにして示す．

1. 単相状態の流体がある程度以上の緩和時間を持つ場合，一様分散した粒子が配列を形成する．
2. 非ニュートン性流体であっても，緩和時間が小さい場合，その実効粘度は式(1)と同等の値を示す．
3. 粒子配列が形成される領域では，その比粘度が式(1)で見積もられる比粘度より小さい値を示す．
4. 粒子配列が形成される領域では，その粒子配列の度合い（長さ）に従って，比弾性が増加する．

このように，単相状態における分散媒の緩和時間は分散した粒子の配列形成の要因となり，形成された粒子配列は巨視的視点における実効的な粘弾性を変調させるという，連鎖的因果関係が明らかとなった．さらに非定常なせん断振動を加えている間，一度形成された粒子の配列状態は維持されることから，配列された粒子の間には弾性の効果による復元力が働いているものと推察できる．粒子間に弾性的効果が存在するのであれば，巨視的な実効弾性が配列粒子の度合いで増加することについて，帰納的に説明づけられる．

4.　トイモデルによる数値シミュレーション

　粒子を単純なバネで結合したトイモデルを仮定し，粒子配列のパターン形成に粒子間の弾性効果が寄与するか検証した．これにより，分散粒子が配列パターンを形成するために最低限必要となる物理的要素が確認される．高分子溶液の特性を考慮し，復元力が働きうる限界応力も計算の条件として加える．加えて，下記(a)−(f)の条件を設定する．(a)二次元平面空間，(b)初期粒子配置は一様乱数．粒子直径と等価の厚みを有した円盤体積を母数として，粒子総数から体積率を計算．(d)粒子は流れに追従し，粒子の運動による流体への影響は考慮しない．(e)軸対称，かつ周方向一方向流れ（ニュートン性流体における解析解）．(f)非弾性衝突で，粒子の回転による慣性力は考慮しない．∆t時間ステップで流動による全粒子の変位を仮決定し，粒子間距離が増加した場合のみ，粒子間にバネ係数k_pによる復元力を粒子に与える．この時，計算される力が臨界値k_Yを超える場合はベクトル演算に加えない降伏条件を考慮している．計算対象の粒子を中心が1となるように，二次元のガウス分布係数を粒子間に働く力の総和計算時に重みづけとして与える．これらの計算の結果，単位時間内に加わる力積から粒子の変位を与えた変位を再計算させる．その他，詳細な計算過程は文献[6]を参照いただきたい．

　動画1にトイモデル計算で得られた，振動周期1サイクル後の粒子配置を示す．粘弾性流体における実験（例えば，図3b上）とほぼ同じような，壁面に沿う周方向の粒子配列パターンが再現できている．この計算では，実験に用いた高分子溶液が持つ，せん断速度依存粘度を考慮していない．単純に，弾性の効果と降伏条件のみを粒子間に付与し，現象を再現している．つまり，粒子間距離の変位に応じ，弾性と粘性の比が局所的に変化するような緩和時間の効果と，高分子溶液の持つ降伏応力を考慮することが必要な要素であると理解できる．

Movie 1 Movie of toy model simulation

5.　結　　　言

　緩和時間の異なる非ニュートン性流体，三種に対し，粒子配列現象が与える実効粘弾性変化を定量的に評価した．結果として，流体の緩和時間が分散粒子を配列させる要因となり，形成された粒子配列が巨視的視点における実効的な粘弾性を変調させる，連鎖的因果関係を明らかにした．さらにバネの力を考慮したトイモデルによる検証を通して，配列形成時に働く粒子間の弾性とそのメカニズムについて考察し，緩和時間と降伏条件の重要性が示された．

謝　　　辞

この研究は，日本学術振興会の特別研究員奨励費（18J20516）によって，助成を受けたものである．

文　　　献

[1]	Einstein, A., “Eine neue Bestimmung der Moleküldimensionen”, Annlean der Physik, Vol. 324, (1906), pp. 289-306.
[2]	Rutgers, I. R., “Relative viscosity and concentration”, Rheologica Acta, Vol. 2, No. 4 (1962), pp. 305-348.
[3]	Lyon, M., Mead, D., Elliott, R., and Leal, L., “Structure formation in moderately concentrated viscoelastic suspensions in simple shear flow”, Journal of Rheology, Vol. 45, No. 4 (2001), pp. 881-890.
[4]	Tasaka, Y., Yoshida, T., Rapberger, R., and Murai, Y., “Linear viscoelastic analysis using frequency-domain algorithm on oscillating circular shear flows for bubble suspensions”, Rheologica Acta, Vol. 57 (2018), pp. 229-240.
[5]	Yoshida, T., Tasaka, Y., and Murai, Y., “Efficacy assessments in ultrasonic spinning rheometry: Linear viscoelastic analysis on non-Newtonian fluids”, Journal of Rheology, Vol. 63, (2019), pp. 503-517.
[6]	Yoshida, T., Tasaka, Y., and Murai, Y., “Effective viscoelasticity of non-Newtonian fluids modulated by large-spherical particles aligned under unsteady shear”, Physics of Fluids, Vol. 31, No. 10 (2019), p. 103304.
[7]	Scirocco, R., Vermant, J., and Mewis, J., “Effect of the viscoelasticity of the suspending fluid on structure formation in suspensions”, Journal of Non-Newtonian Fluid Mechanics, Vol. 117, No. 2-3 (2004), pp. 183-192.