流れ　2022年11月号　目次

―　特集テーマ：2022年度年次大会　― 巻頭言 （森，金川） 壁面乱流の工学的モデリング 須賀 一彦 (大阪公立大学) 粉粒体の流れを予測する 田中 敏嗣 (大阪大学) 人工知能をメタモデルとした流体機械の最適化設計 坂口 大作 (長崎大学) 粘弾性流体や乱流拡散を対象とした深層学習 塚原 隆裕 (東京理科大学) モード分解を用いた流体計測の高度化 野々村 拓 (東北大学) 　｜　リンク一覧にもどる　｜

 

壁面乱流の工学的モデリング

須賀 一彦 大阪公立大学

　本稿は日本機械学会2022年度年次大会（2022年9月11日～14日，富山大学）における筆者の基調講演を要約したものである．基調講演と流体工学部門ニュースレターへ掲載する機会を頂いたことに対し，関係各位に心より感謝申し上げます．

１．はじめに

　乱流のCFDが始まって以来，壁面境界を扱うのに対数則を基礎としたものに代表される壁関数法は，産業応用の現場では今なお重宝されてきているが，対数則はよく知られたように適用範囲に限界があるため，様々なアイデアで改良がなされてきた⁽¹⁾．一方で計算機の進歩とともにLESの大規模応用解析が可能になるにつれて，壁モデル⁽²⁾と呼ばれるRANSの壁関数に相当する手法が重要となってきた．この古くて新しい乱流モデルの課題について，筆者の長年の経験からモデリングの基本的な考え方とプロセスを概説し，機械学習との融合について展望する．

２．乱流の壁関数／壁モデル

　まず，CFDコードの中でどのように壁関数が実装されるかについて有限体積法によるRANSを例にとって以下概説する．図１上図の壁面隣接セルP内で変数の壁面近傍で薄層近似した輸送方程式を密度，拡散係数として

(1)

のように記述したとする．有限体積法ではこれをセル内（セル表面をe,w,n,s）において積分し，

	(2)
	(3)

の離散化式を得る．ここではセルP内の生成項の平均値である．式(3)中のはが壁面に平行なx方向の速度成分() の場合に壁面せん断応力に対応し，温度() の場合には（壁面熱流束）に対応する．壁面に垂直なy方向の格子間隔が十分細かければ，これらの値を壁面境界上のの値を用いた離散式で記述して問題ないが，境界層内で粗い格子を用いると十分な精度が期待できない．そこで，対数則を用いた関数式によりやを代数的に与えるのが標準壁関数モデルである．たとえば，速度場においてカルマン定数κ，B=5~5.5とする対数速度分布が点Pで成立するとして繰り返し計算の中で(N+1)ステップ目の値をと与える．以上の手続きは一般的な三次元の輸送方程式に容易に拡張できる．なお，上付き文字+は壁座標無次元値，添え字Pは点Pでの値を意味する．LESでも対数則を用いる壁モデルでは同様の手続きを行っている．

　また，セルPを壁面垂直方向に細分化した無数のサブセルを仮定し，対数則などの経験則を適用しないで，離散式(3)の右辺第1項をy方向にだけサブセル上で再度差分して解く方法もある．RANSでは数値的壁関数(Numerical Wall Function)⁽³⁾と呼ばれるが，LESでは非平衡壁モデルの実装に使われる手法である．

３．解析的壁関数モデリング

3.1　基礎式
　以上のように古典的な対数則壁関数は，壁面境界条件として壁面せん断応力を平均速度の対数則を用いて与える方法であるが，対数則の成立しない流れ場には精度を欠くことを免れない．そこで，薄層近似した輸送方程式

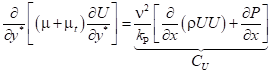(4)

を壁面隣接セル内で積分して，境界条件を与える解析的壁関数(Analytical Wall Function: AWF)⁽⁴⁾が提案された．ここでは，それぞれ平均圧力勾配，粘性係数，渦粘性係数，動粘度，乱流エネルギーであり，無次元距離はとしている．渦粘性係数は図１下図の破線のように壁面近傍では壁からの距離の3乗に比例して減衰するが，これを粘性底層厚さ以下では無視し，に関する区分線形関数でモデル化し，かつ有限体積法の常であるように式(1)の右辺をセル内で一定とすると，式(4)は常微分方程式に帰着し，数学的（解析的）に積分できてセルP内で速度分布や壁面せん断応力などの境界条件を代数的に与えることが可能となる．ここで，は散逸長さスケールの係数と渦粘性モデル係数の積=2.55×0.09である．なお，温度や濃度などのスカラー場も同様な考え方で壁面境界を与えることができる．

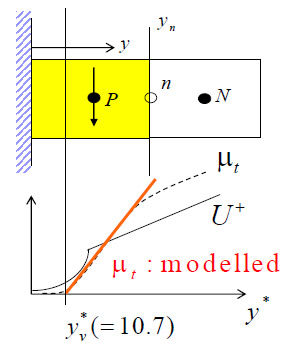
Fig.1 Near-wall cells and simplification of the near-wall eddy viscosity distribution.

3.2　モデルの拡張
　AWFモデルの核心は壁面近傍の渦粘性分布を壁面距離の単純な関数でモデル化することにあるので，流れ場の特性に対応して渦粘性分布をの適切な関数で表現してやれば良いことになる．例えば，粗面では見かけ上粘性底層が埋没し現れなくなるので粗さ高さに応じて粘性底層厚さを小さくし，場合によっては負の値を持たせることでとした⁽⁵⁾．ここで，は滑面の粘性底層厚さであり，は粗さ高さであるが，は参照データとの対応を試行錯誤して決定したモデル係数である．しかし，AWFによって図2のようにMoody Chartを再現し，その他のより複雑な流れ場でも精度の高い予測をすることができている⁽⁵⁾．

　また，高プラントル／シュミット数流体のスカラー輸送問題については，渦粘性係数の粘性底層内での漸近挙動をより正確に模擬する必要が出てくる．そこで，壁面近傍の粘性底層では，モデル係数βを与えて，として基本モデルのと連結する分布に修正することで，図３のようにPr＝1000でも修正しない場合（図中Gerasimov）と比べてKaderの実験式をよく再現することができている⁽⁶⁾．

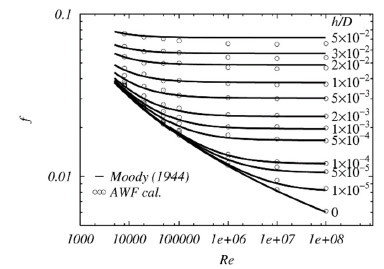
Fig.2 Friction factor of pipe flows depending on roughness height/pope diameter:( Moody Chart)

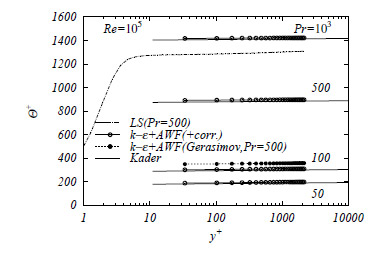
Fig.3 Turbulent thermal fields at high Prandtl number fluids. LS: low Re simulation without WF, Gerasimov: basic AWF, Kader: experimental correlation.

　一方，渦粘性乱流モデルを衝突流れ解析に応用する場合，よどみ点の様にひずみ速度の大きい領域で過剰な熱伝達が予測される傾向にあり，この対処としてひずみ速度に依存して渦粘性係数を小さくすることが有効であると知られている．そこで，モデル係数をとひずみ速度不変量の関数とすることで，壁に沿った流れだけでなく衝突流れにおいても図４に示すように妥当なNu数分布を予測できるようになる⁽⁷⁾．

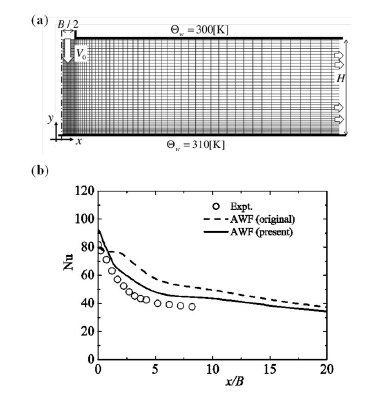
Fig.4 Imping jet heat transfer at Re=20000, H/B=9.2.

3.3　LESへの展開
　AWFのLES拡張に際しては，フィルター化操作をで表して，式(4)に対応した

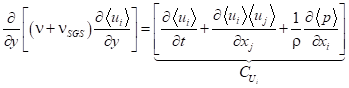(5)

を積分する⁽⁸⁾．ここで，RANS同様に渦動粘性分布は，スマゴリンスキーモデルではテストフィルターを使って見積もったを用いた無次元距離のシンプルな関数形で模擬する．ただ，粘性底層厚さは試行錯誤による検討から，SGS乱れとGSの時間スケール比の関数としている．この壁モデルは式(5)右辺に非平衡成分を陽に含むので，代数型非平衡壁応力モデルに分類される．

　このようにしてLESに拡張したAWFを1方程式SGSモデル⁽⁹⁾に組みこんで，リブ付きチャネル流れで評価した結果を図５に示す．図から壁面第1格子高さがリブ高さの５～１５％になるような粗い計算格子を用いても，詳細な格子を用いたLESの結果⁽¹⁰⁾と比較してAWF-LESは遜色のない速度場の統計を得ることが示されていいる．また，解の格子の依存度も小さく，実用的な計算に大いに役立つことが分かる．

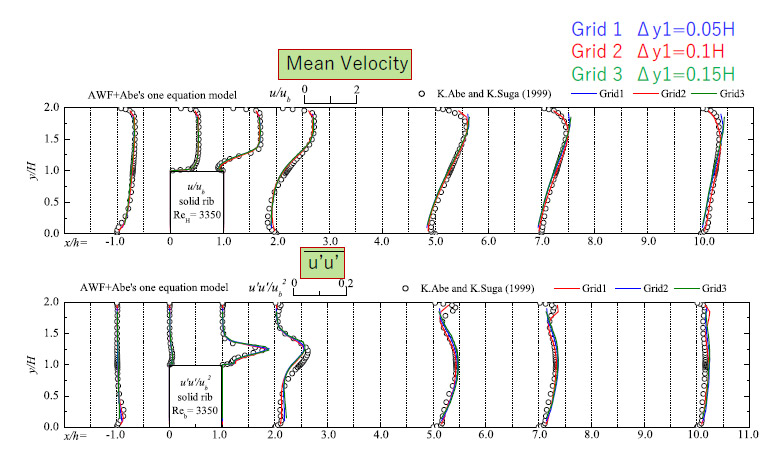
Fig.5 Performance of the AWF-LES in a rib-mounted channel flow.

４．今後の展望

　壁関数モデルなどの乱流のモデリングは，次元解析，数学的整合性，支配される物理モデルなどの考察によって，その骨組みが決定され，最後にモデル係数（関数）は実験などの参照データとの対比で決定されてきた．この最後のプロセスが古くは研究者の豊富な知識もしくは直観に頼ってなされてきた．実際，渦粘性のモデル係数や散逸率方程式のモデル係数，などの導出は実に美しいと思う．しかし，著者が携わるようになった90年代からは，DNSによる豊富なデータが入手できるようになったことで，主として試行錯誤による最適化に置き換わってきた．したがって，モデル係数は定数ではなく，時として（怪しげな）関数で表現され，関数形に特に物理的意味はないので，よく単なる合わせ込みではないかと揶揄する向きもあった．（一部，的を得ている．）しかしながら，結果として得られた乱流モデルはベンチマークテスト以外の応用場でも実力を発揮して，実用に供してきたと思っている．このような我々が時として行った，膨大なベンチマークデータとの突き合せによる試行錯誤による最適化は，そっくりそのまま機械学習に置き換えられる筋のものである．たとえば，本稿で現れたモデル係数αは流れ場の状況によって変化するべき係数であるが，これを機械学習で求めるようにするだけでより可能性が広がるはずである．

　つまり，今後の「正統な」乱流モデリングは，次元解析，数学的整合性，支配される物理モデルなどの考察の上にデータサイエンスを駆使したモデル係数の決定からなっていくものと断言できる．数学や物理モデルのない単なる機械学習だけでは，いわゆる外挿に相当する実問題への対処に難点が残ったままになると考えられる．

参考文献

(1)	須賀一彦，RANS乱流解析のための解析的壁関数モデルの進展，ながれ, 35 (2016) pp.247-254.
(2)	Craft, T.J., Gant, S.E., Iacovides, H., Launder, B.E., A new wall function strategy for complex turbulent flows, Num. Heat Transf. B, 45 (2004), pp.301- 318.
(3)	Larsson, J., Kawai, S., Bodart, J., Bermejo-Moreno, I., Large eddy simulation with modeled wall-stress: recent progress and future directions, Mech. Eng. Rev., 3 (2016), 15-00418.
(4)	Craft, T.J., Gerasimov, A.V., Iacovides, H., Launder, B.E., Progress in the generalization of wall-function treatments, Int. J. Heat Fluid Flow, 23 (2002), pp.148-160.
(5)	Suga, K., Craft, T.J., Iacovides, H., An analytical wall-function for turbulent flows and heat transfer over rough walls, Int. J. Heat Fluid Flow, 27 (2006) pp.852-866.
(6)	Suga, K., Computation of high Prandtl number turbulent thermal fields by the analytical wall-function, Int. J. Heat Mass Transfer, 50 (2007) pp.4967-4974.
(7)	Suga, K., Ishibashi, Y., Kuwata, Y., An analytical wall-function for recirculating and impinging turbulent heat transfer, Int. J. Heat Fluid Flow, 41(2013) pp. 45-54.
(8)	Suga, K., Sakamoto, T., Kuwata, Y., Algebraic non-equilibrium wall-stress modeling for large eddy simulation based on analytical integration of the thin boundary-layer equation, Phys. Fluids, 31 (2019) 075109.
(9)	Abe, K., An improved anisotropy-resolving subgrid-scale model with the aid of a scale-similarity modeling concept, Int. J. Heat Fluid Flow, 39(2013) pp.42-52.
(10)	Abe, K., Suga, K., Large eddy simulation of passive scalar in complex turbulence with flow impingement and flow separation, Heat Transf. Asian Res., 30 (2001) pp.402-418.