流れ 2022年11月号 目次
― 特集テーマ：2022年度年次大会 ―
｜ リンク一覧にもどる ｜ |
人工知能をメタモデルとした流体機械の最適化設計
|
１．はじめに
コンピュータに形状探索を全自動で実行させ，少ない時間的コストで複数の目的関数について最適形状を導きだすことができる多目的最適化設計(1)が応用されつつある．解析精度が保証されたCFD利用を基本として，形状変更，計算格子の生成，境界条件の設定，数値解析ソルバーおよびポスト処理までを全自動化し，Fig.1に示すようなターボ機械のような複雑形状も短時間に検討・評価できるものである．
本稿では，形状探索方法として遺伝的アルゴリズムを用い，CFDの代替モデル（メタモデル）として，人工知能（ニューラルネットワーク）を利用した多目的最適化システムの概要を解説する．
Fig.1 Example of optimization target by multi-objective optimization (2,3)
２．遺伝的アルゴリズムおよびニューラルネットワーク
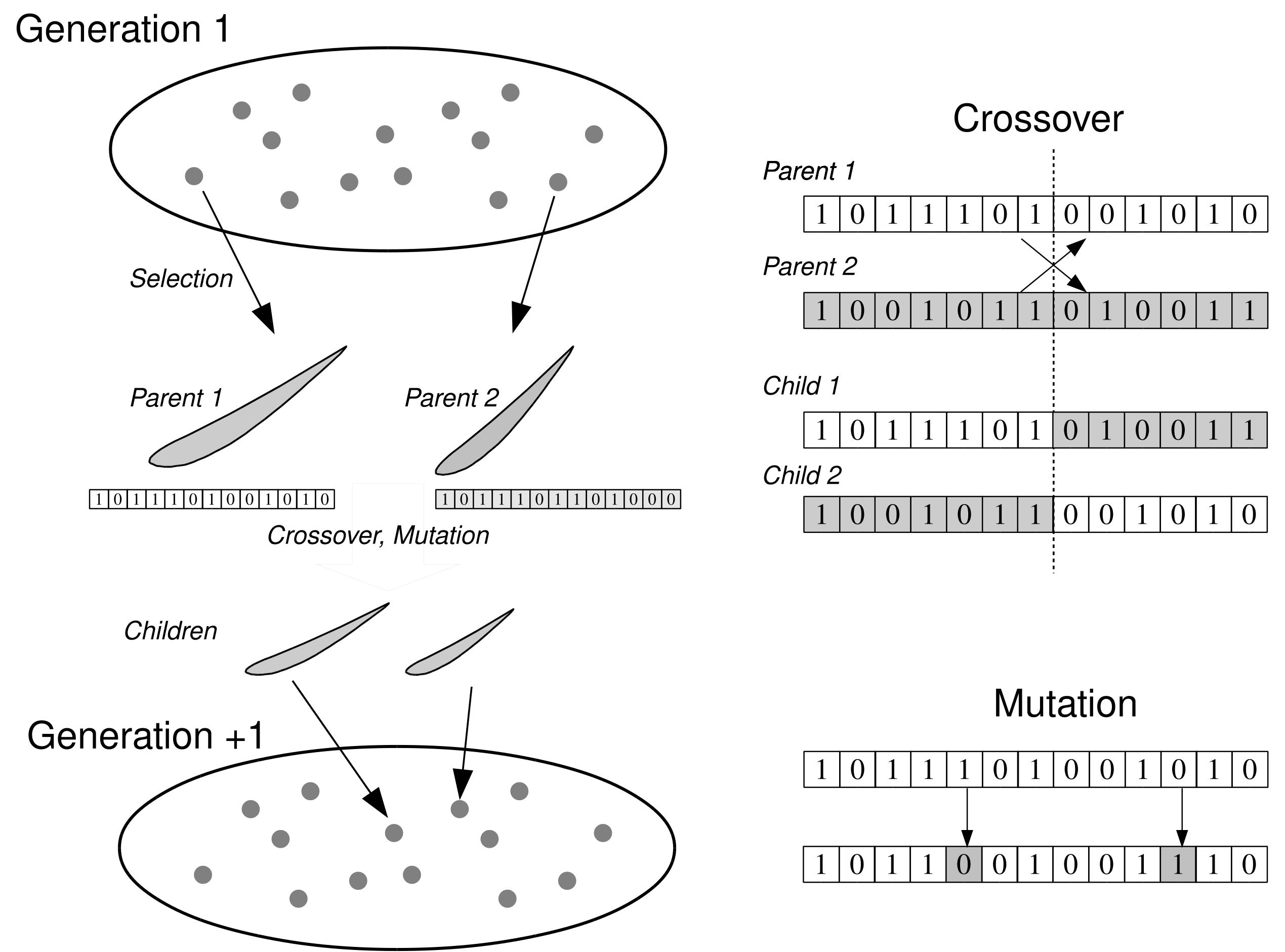
様々な形状パラメータの組み合わせの中から，最適な形状を見出す手法として，Fig.2に示す遺伝的アルゴリズム（GA：Genetic Algorithms）が良く用いられる．人口と呼ばれる解の集団を作り，これを構成する個体と呼ばれる解候補群が，選択，交叉，突然変異という過程を繰り返しながら最適解へと収束していく．
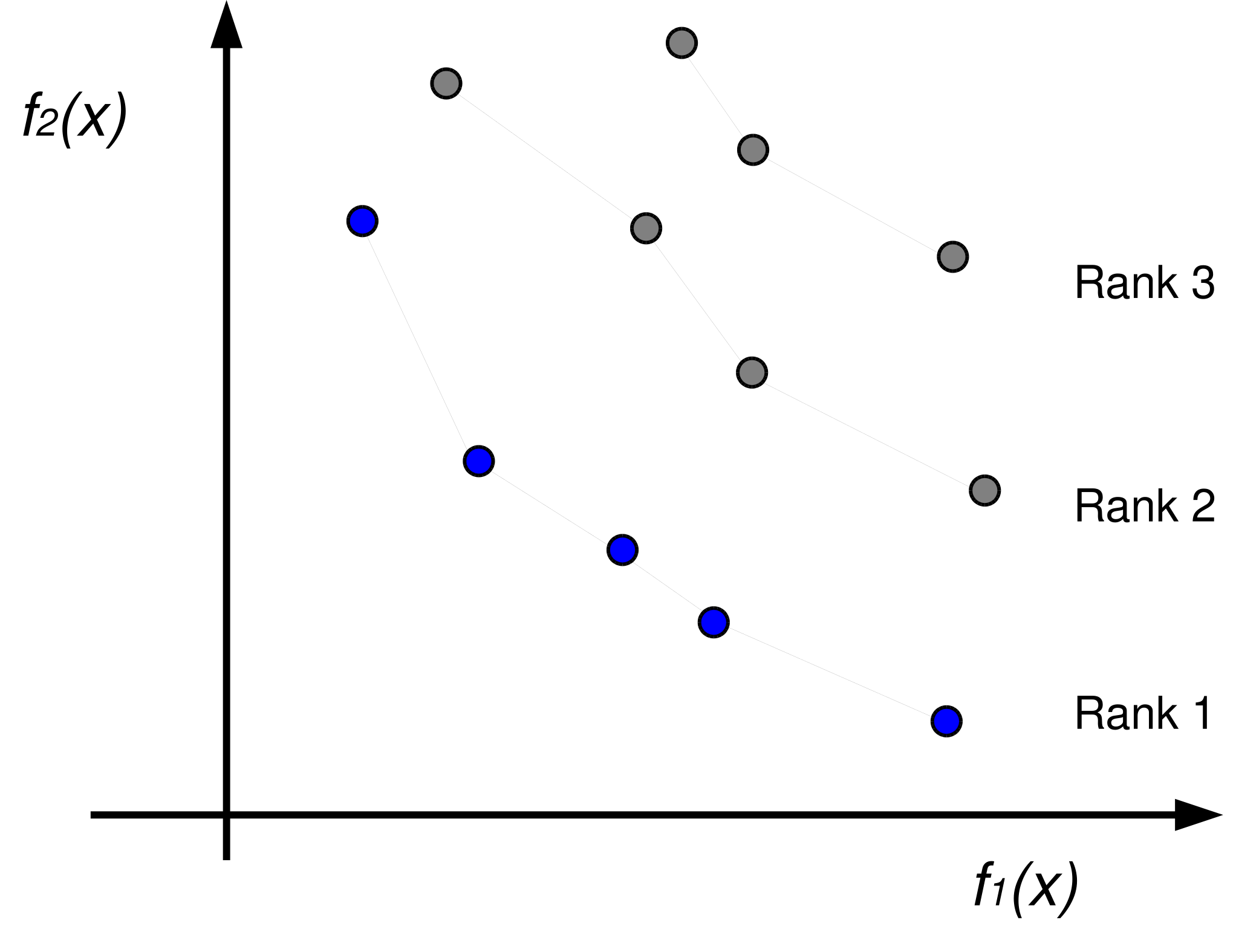
遺伝的アルゴリズムでは，良好な組み合わせによる子孫であるかどうかという評価を行う必要がある．多目的最適化の場合，評価された解はランキング処理され，Fig.3に示すようなランク１の個体について新たな世代の組合せが実行される．
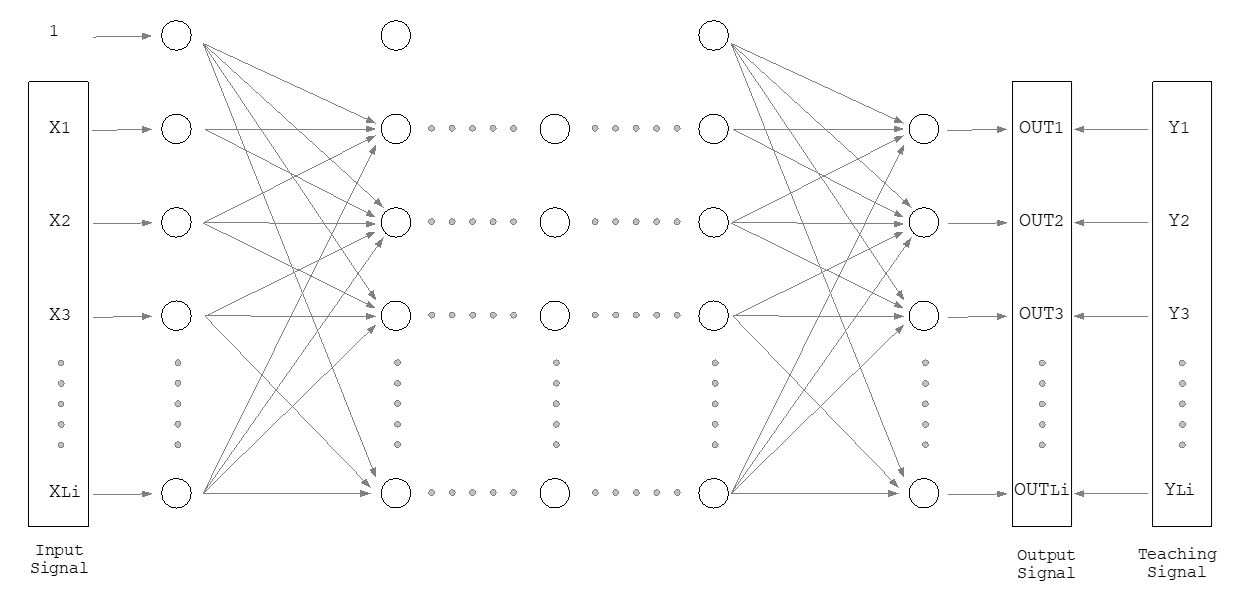
しかし，一般に組合せ数は非常に多くなり，評価にCFD解析を用いると計算コストが莫大になってしまうという問題がる．そこで，進化アルゴリズムの計算コストを削減する方法として，メタモデルが導入された．メタモデルには応答曲面法，放射基底関数回路網およびクリギングなどが提案されており，本最適化システムでは，ニューラルネットワークを採用した．Fig.4に一般的な階層型ニューラルネットワークを示す．入力層から入力されたデータは，中間層（隠れ層）を通り，各ニューロンで伝達関数に基づいた重みを付加した信号を伝達して出力層へ出力される．ニューラルネットワークは，教師信号に基づいた判断を行うので，学習するデータ数を増やし，再学習することで予測精度を改善することができる．
|
|
Fig.2 Genetic algorithms |
Fig.3 Pareto ranking process for a two objective optimization problem |
|
Fig.4 Artificial Neural Networks |
３．多目的最適化設計システム
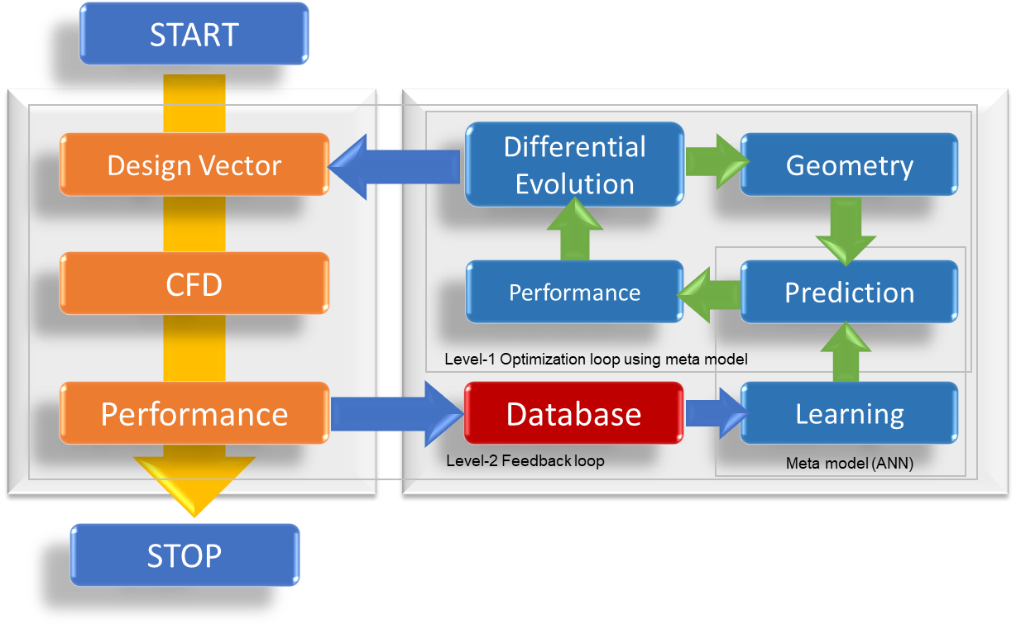
本研究で用いた多目的最適化設計システム(4)の概略をFig.5に示す．まず，初期データベースを構築するために，実験計画法(DOE : Design of Experiment) に基づいたパラメータスタディを行う．次いで，学習されたメタモデルを用いて最適化ループ(Level 1 Loop)を実行し，遺伝的アルゴリズムにより最適解の候補を得る．最適解の候補の中から代表複数個体に対してCFDによる精度の高い評価 (Level 2 Loop)を行い，データベースの再構築およびメタモデルの再学習を行う．メタモデルによるレベル1のループおよびCFDによるレベル2のループを繰り返すことでデータベースが更新され，メタモデルはより高い精度で最適解を見出すことができるようになる．多目的最適化では，パレートフロントの更新が収束するまでレベル1およびレベル2のループが繰り返し実行される．
|
Fig.5 General layout of the meta-model assisted optimization system (4) |
４．ターボ機械における多目的最適化設計
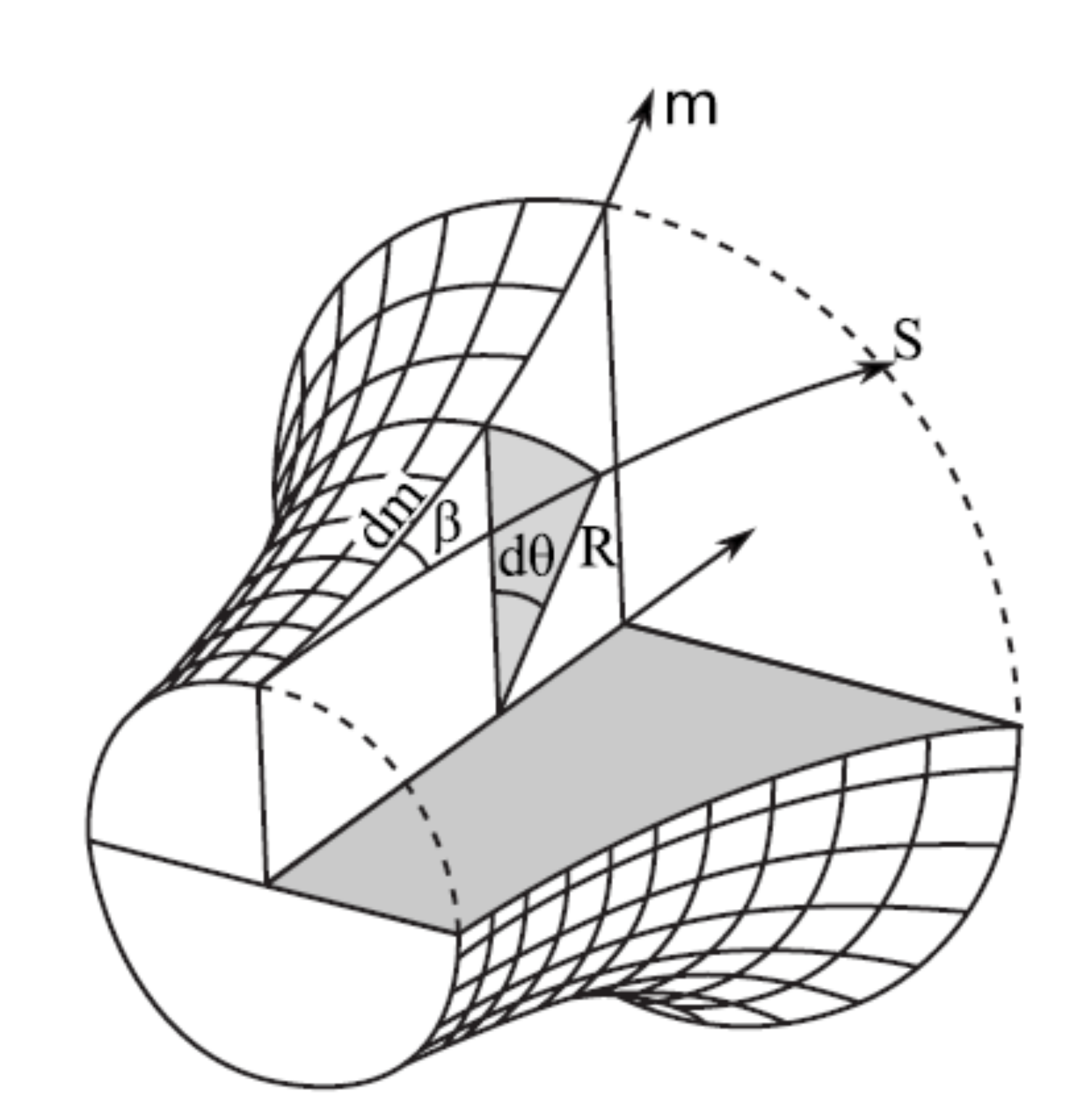
ターボ機械は3次元的に形状が複雑であり，形状再現には特別な工夫が必要である．Fig.6にターボ機械における子午面距離
および羽根に沿う流れ方向
の幾何学的関係(5)を示す．羽根の角度を
，巻き角を
とすれば，半径
の位置における幾何学的関係は以下のようになる．
|
(1) |
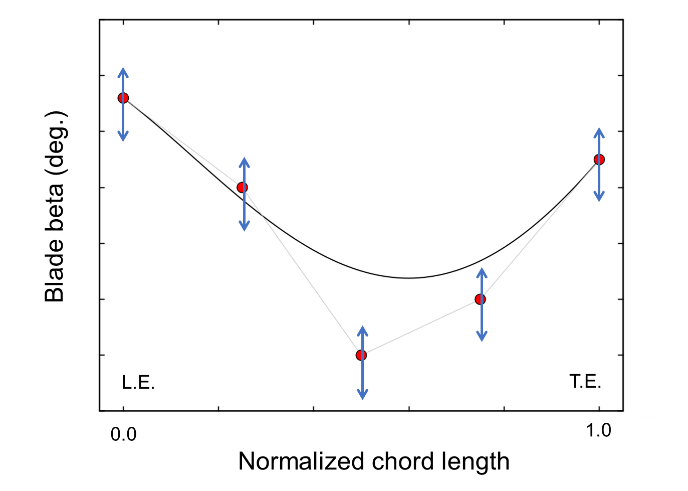
羽根の角度は前縁から後縁にかけて滑らかに分布している場合が多いので，Fig.7に示すようにコントロールポイントをコード長内で配置し，ベジェ曲線で滑らかな羽根角度分布を再現した．各コントロールポイントで，一定の範囲だけ角度を変えることをでき，コントールポイントの上限および下限内で最適形状を探索することになる．なお，コントロールポイントの配置数および配置位置は等間隔である必要はなく，流れの特性に合わせて配置することが必要となる．スパン断面において，反り線で定義された羽根角度分布に羽根厚み分布を加え，子午面および式(1)の関係を考慮して羽根形状を3次元的に生成する．
|
|
Fig.6 Geometry definition of the camber-line by blade angle |
Fig.7 Blade angle distribution from leading edge to trailing edge generated by Bezier control points |
and circumferential position 
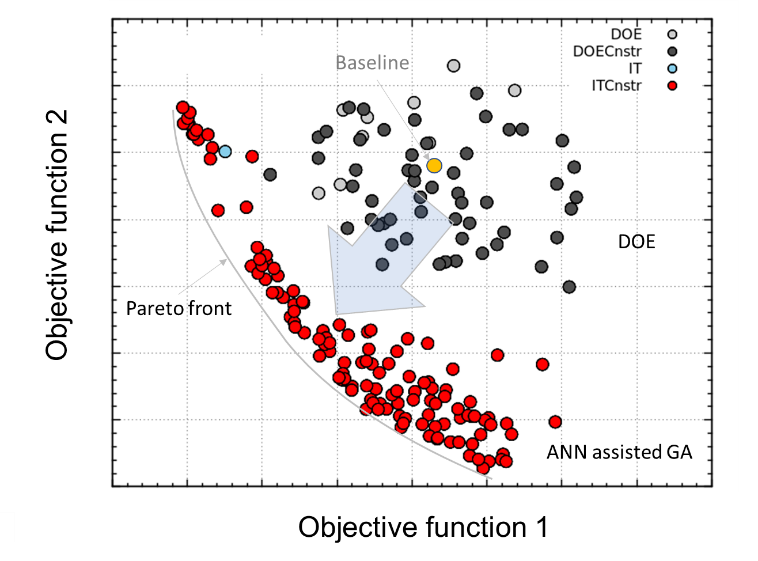
of a radial compressor Fig.8にターボ機械を最適化設計した際のパレート解の一例を示す．2つの目的関数は背反関係にあり，遺伝的アルゴリズムによる探索した個体群は，最小化問題として明瞭なパレート解を示している．パレート解上の個体はすべて最適形状と言え，２つの目的関数の重みに応じて，設計者が最適形状を絞り込む．
|
Fig.8 Design individuals on two-objective space searched by DOE and ANN assisted GA |
５．まとめ
ニューラルネットワークをメタモデルとし，遺伝的アルゴリズムにより形状探索を実時間で行える多目的最適化システムを紹介し，ターボ機械設計上の工夫について解説した．ターボ機械設計は，取り扱うパラメータが多いことが設計を難しくしているが，最適化システムを用いることで，コンピュータに自動で形状探索させ，時間的開発コストを下げることができる．さらに，本稿で紹介したようなニューラルネットワークなどのメタモデルを用いることで，効率的な探索が可能となる．多目的最適化設計は，単に最適形状を見出すだけでなく，形状探索時に検討した形状データを再整理することで，設計パラメータの重要性が理解でき，設計ノウハウの構築にも役立つ．
最後に，2022年度年次大会にて本内容を紹介させていただき，ニュースレターでその概要を報告させていただける機会を与えていただきました．あらためまして，関係者各位に謝意を申し上げます．