流れ　2022年11月号　目次

―　特集テーマ：2022年度年次大会　― 巻頭言 （森，金川） 壁面乱流の工学的モデリング 須賀 一彦 (大阪公立大学) 粉粒体の流れを予測する 田中 敏嗣 (大阪大学) 人工知能をメタモデルとした流体機械の最適化設計 坂口 大作 (長崎大学) 粘弾性流体や乱流拡散を対象とした深層学習 塚原 隆裕 (東京理科大学) モード分解を用いた流体計測の高度化 野々村 拓 (東北大学) 　｜　リンク一覧にもどる　｜

 

粘弾性流体や乱流拡散を対象とした深層学習

塚原 隆裕 東京理科大学

１．緒言

　本研究では様々な乱流現象の内から，乱流摩擦抵抗低減効果を呈する粘弾性流体チャネル乱流の構成応力場（§2）と，ニュートン流体チャネル乱流におけるスカラー濃度乱流拡散（§3）を研究対象として取り上げる．それらの膨大な瞬時場データ，いわゆる乱流ビッグデータ⁽¹⁾を機械学習により推論し，各種予測の実現を目指している（図1）．より本質的には，乱流現象に内在する物理の予測，もしくは外部境界条件の予測の可能性を，機械学習に見出す試みである．

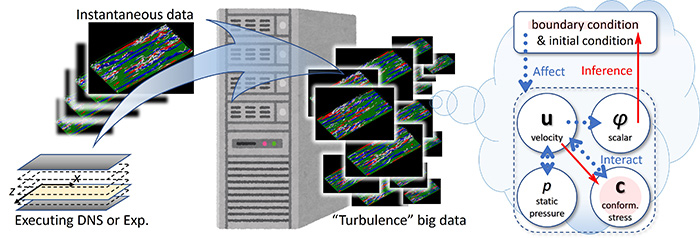
図1　乱流ビッグデータに基づく内在物理や外部条件の推論

　チャネル乱流は平行平板間の圧力勾配駆動流れの乱流を指し，元来，十分に高いレイノルズ数であれば統計的定常状態にあって，つまり一種の平衡状態にある．乱流物理の解明にあたって従来研究では平衡状態を対象に，その統計量を算出し壁乱流の本質の理解が多く試みられてきた^(2-4)．一見無秩序に見える乱流場の微小な乱れ（ゆらぎ）や渦の一つ一つについては，壁乱流の自己維持機能に関わるもの以外には，均されてしまうことが常である．実際にも工学的要求に対しては，主流や積分スケール程度の乱れの把握が肝心であり，瞬時変動場はサブグリッドスケールモデル等で適切にそれらによる輸送量が評価できれば，事足りることも多い．乱流のエネルギーカスケードの観点からも，積分スケール相当の低波数領域（大きい渦）ではバルク流路に対する依存性が強い一方で，慣性小領域以降の高波数領域（小さい渦）においては統計的普遍則が成り立つために，それら瞬時の状態などへの更なる関心は払われていない．つまりは，統計的特徴に基づいて壁乱流の本質理解や状態予測は行われてきたが，ここで機械学習の援用により瞬時場から有意な特徴量抽出の可能性を議論したい．チャネル乱流も瞬時・局所に捉えれば乱流生成・拡散・散逸が間欠的に生じる非平衡状態にあり，一見して無秩序に千差万別な乱れと渦にも有意な特徴を含有しているであろう．統計処理によって均される（失われる）瞬時場独自の特徴が抽出できれば，時空間的に限られた情報から内部（内在する物理）や外部（初期条件・境界条件）を予測することも可能と期待する．この実現には，データ同化⁽⁵⁾やスパースセンシング⁽⁶⁾などの様々なアプローチは存在するが，チャネル乱流の直接数値計算（DNS）などにより必然的に時々刻々と瞬時場データは蓄積され，膨大な乱流ビッグデータを活用しやすい環境（時代）となった今，改めて人工ニューラルネットワークによる深層学習の可能性を調査し，ここでは冒頭で挙げた2例の試みを報告する．

２．内在物理予測：粘弾性流体乱流の構成応力場推定

　第一に挙げるは，非ニュートン流体の一種，粘弾性流体の構成応力場に関する推論である．この流体は，摩擦抵抗低減効果をもたらす稀薄界面活性剤水溶液または稀薄高分子水溶液を想定している．その抵抗低減メカニズムの解明や，高レイノルズ数・高ワイゼンベルグ数における高負荷かつ数値不安定なDNSの一部代用を目指している．通常，DNSでは構成応力の計算にFENE-PモデルやGiesekusモデルなどの構成方程式を用いるが，高ワイゼンベルグ数における数値不安定性が度々問題となる⁽⁷⁾．そこで，構成方程式に代る深層学習ベース代理モデルを構築し，数値不安定性の解決を試みる．本研究では，Giesekusモデルに基づく粘弾性流体チャネル乱流を解析対象として畳み込みニューラルネットワーク（CNN）により学習させ，代理モデルに瞬時速度場から同時刻の瞬時構成応力場を予測させ，DNS-CNN統合計算（速度場計算はDNS）の実用可能性の調査を行った．

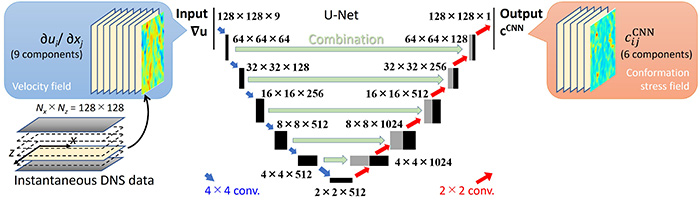
図2　U-Netのアーキテクチャと入力および出力データ

　深層学習のモデルには，CNNの一種で，空間情報を保有したまま特徴抽出が行えるU-Net⁽⁸⁾を用いる（図2）．入力と出力には，それぞれ速度勾配テンソル∂_ju_iの9成分と構成応力c_ijの1成分として，チャネル壁に平行な面情報で学習・予測を行う．このとき，壁面垂直方向位置に依らず単一の学習器としている．周期境界を課した計算領域サイズは，チャネル幅2δに対して主流方向とスパン方向には6.4δ × 3.2δの面積を有する．壁垂直方向の格子数はN_y = 192であり，かつ100瞬時場分のデータを用意し，合計N_y × 100 = 19200の画像枚数を学習させた．

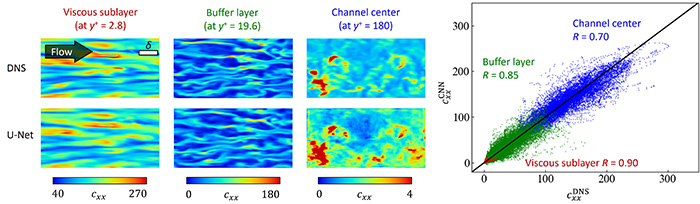
図3　学習済みU-Netによる瞬時速度場からの同時刻・同位置の構成応力場の予測．左：壁からの高さ別の結果（c_xxは構成応力の主流方向垂直成分，y⁺は壁法線方向距離を壁単位で表し，y⁺ = 180は流路中心に等価）． 右：DNSと予測値の比較散布図と相関係数R．

　図3は，摩擦レイノルズ数180と摩擦ワイゼンベルグ数10における主流方向構成応力c_xxのDNS（真値）とU-Net予測による結果比較である．同一の学習器でありながら，粘性底層，バッファ層，およびチャネル中央部それぞれの特徴が，定量的にもよく予測されていることが分かる．真値との相関係数も0.7～0.9と高い値を示すが，バッファ層の強い局所変動に対してU-Netによる過小評価の傾向が見られた．これは，壁近傍構造の強い縦渦がバッファ層で支配的であり，その縦渦が必ずしも予測平面内に存在しないこと（入力情報に含まれないこと）に起因すると考えられる．その他の構成応力成分やレイノルズ数においても予測精度は同様の傾向である⁽⁹⁾．

動画1　DNS-CNN統合計算による粘弾性流体チャネル乱流の再現

　上記の学習済みU-Netを用いたDNS-CNN統合計算（速度場の計算はNavier-Stokes方程式に基づく）は，動画1のように安定して実行され，DNSに近い統計量が得られることを確認している⁽¹⁰⁾．図中のRMSE（二乗平均平方根誤差）は，最初に初期条件でもあるDNS（真値）から徐々に外れてはいるものの，1.0程度で収束しており，これはそもそもの乱流強度と同程度である．いわゆる，カオスのように僅かな差異への鋭敏依存性に起因するもので，このRMSEの値は本質的な問題ではない．また，前述のバッファ層における局所変動の過小評価は，代理モデルによる計算において致命的ではないと言える．

３．外部条件予測：乱流上流にあるスカラー拡散源の推定

　瞬時・局所の限られた濃度分布情報から即座に物質拡散源を特定するような逆問題の解決は，海洋や化学プラントなどで重要なタスクである．前者（海洋）の具体例としては海底鉱物資源が眠る熱水鉱床の探索において，後者については有害物質の漏洩事故が起きた際の迅速対応において，新たな手法が必要とされる．特に，過酷環境下または有害物質漏洩の場合，拡散源への接近は困難となり，下流遠方の濃度分布情報に基づいて拡散源までの距離を推定する，もしくは拡散源位置と排出量を即座に見積もる技術が要求される．さらに，その多くは乱流環境下での計測になるため，難易度が一層増している．そのような技術的要求に応える一案として，瞬時二次元情報（画像）から特徴を抽出し推論ができる深層学習を応用し，乱流スカラー拡散における下流濃度情報からの拡散源推定が可能なCNN学習器の構築を試みてきた⁽¹¹⁾．

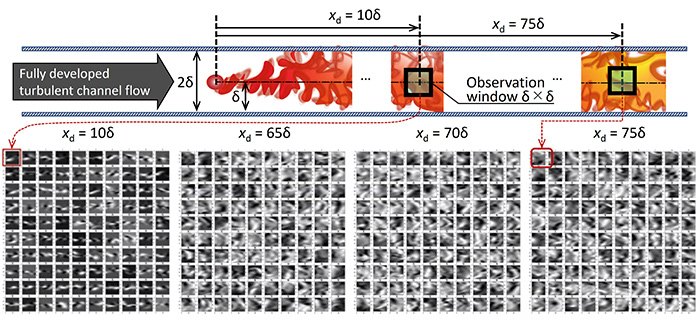
図4　チャネル乱流中の点源からのスカラー乱流拡散と，各下流位置の観測窓で得られたサンプル画像．

　検証の場は，チャネル乱流における定常点源からのスカラー拡散である．図4の模式図に示すように，点源下流にある有限サイズの観測窓における瞬時濃度分布（画像）から，その拡散源までの距離x_dを推論する．複数の観測位置を設けて，濃度分布画像から観測位置を判別（分類または回帰予測）することがタスクである．

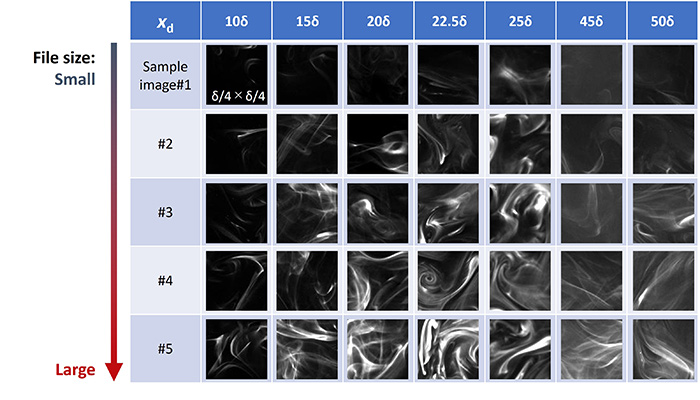
図5　PLIFによる染料拡散画像．
Fig. 5: Image samples of dye plume pattern, used for validation of our pretrained CNN.

　訓練画像および検証画像は，チャネル水路実験で蛍光染料を用いたPLIF（planar laser-induced fluorescence）画像⁽¹²⁾，またはDNS⁽¹³⁾によって用意した．図5は各x_dにおけるPLIF画像の一例であり，いずれも学習済みCNN（GoogLeNet⁽¹⁴⁾がベース）により判定精度80%以上で認識ができたものである．情報量の指標にもなるJPG形式ファイルサイズに違いはありながら，拡散源距離推定においての特徴情報量としてはいずれも変わらないことが示唆される．その特徴量の特定は，今後の課題である．

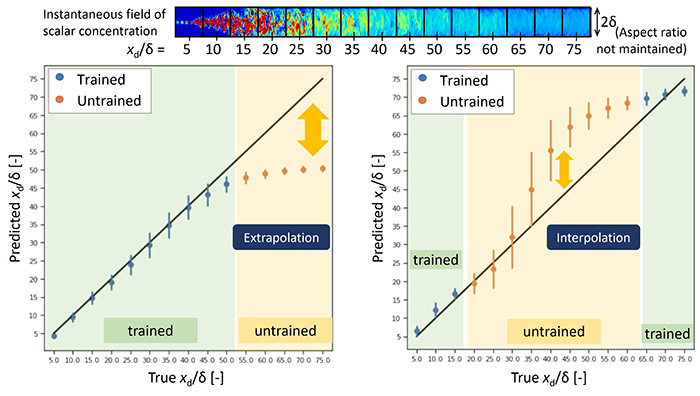
図6　訓練済み・未訓練クラスの推定結果．左）外挿予測，右）内挿予測．

　DNSから得られた画像群（図4）を学習させたCNNに，訓練に用いていないデータ画像での検証で推定精度は100%に近い結果が得られたが，図6に示すように，未学習クラスの内挿予測または外挿予測をさせると有意に精度は低下した⁽¹³⁾．これの改善にも，学習器が瞬時局所情報から抽出している特徴量の特定を進める必要があろう．より詳細には，CNNアーキテクチャ依存性，画像サイズ依存性，画像の回転・拡大縮小およびノイズに対するロバスト性に関する検証について既報を参照されたい⁽¹⁵⁾．

４．結言

　深層学習を用いて，瞬時局所情報に基づく速度場から構成応力場の推定，および下流濃度分布から拡散点源位置の推定を実証した．統計量では失われる瞬時局所情報の有用性の一端を示し，深層学習による粘弾性流体代理モデルや拡散源推定ツール構築の可能性を確認することができた．また，学習済みCNNによる代理モデル計算により，数値計算上の不安定化を回避できる可能性が見えてきた．時空間的に局所の強い変動（rare event）の取扱い，未学習領域の外挿予測のみならず内挿予測まで，未だ課題は多く残る．学習精度の向上は勿論のこと，学習可能限界を見出すことは，内在する物理の解明や，外部予測時のデータ収集指針にも繋がるため，今後の研究（乱流ビッグデータの機械学習）にも大いに期待がかかる．

　本研究では，既存アーキテクチャを利用させて頂いている．上記の結果は，最新のニューラルネットワークの利用で更なる改善も期待できるが，本質的に重要なことは単に推定精度の向上ではない．代理モデル構築であれば数学的実現性や物理学的法則に反しない推論を保証すべきで，状態認識であれば特徴量の特定が肝心な課題である．これらには，PINN（Physics-Informed Neural Network）やGAN（Generative Adversarial Network）なども有効であろう．

謝辞

　研究協力者である東京理科大学大学院生の石神隆寛君，栗原稔幸君，田代雅哉君に謝意を表する．本研究において，大阪大学サイバーメディアセンターの大規模科学計算システムを利用した．本研究は，JSPS科研費基盤 (A) 18H03758，(S) 21H05007（研究代表はいずれも深潟康二先生（慶應義塾大学））の助成を受けて行われたものである．

　最後に，当記事は日本機械学会2022年度年次大会にて開催された「EFDワークショップ：流体工学とAI」での講演内容を，僭越ながらニュースレターにて要約し報告させて頂くものである．長年に亘るEFDワークショップのコーディネータの先生方，特にこの度も幹事をされた飯尾昭一郎先生（信州大学），渕脇正樹先生（九州工業大学），稲澤歩先生（東京都立大学），菊地聡先生（岐阜大学）に敬意を表したい．また，ニュースレター執筆の貴重な機会を与えてくださった金川哲也先生（筑波大学），森英男先生（九州大学）をはじめ，流体工学部門の広報委員会に感謝を申し上げる．

文献

(1)	深潟康二，深見開，“機械学習を用いた乱流ビッグデータ解析に向けて”，計測と制御，59巻8号（2020年8月掲載），pp. 571–576．
(2)	笠木伸英（総編集），河村洋，長野靖尚，宮内敏雄（編），乱流工学ハンドブック (2009)，pp. 191–200，207–215，朝倉書店．
(3)	Smits, A. J., McKeon, B. J., and Marusic, I., “High–Reynolds number wall turbulence,” Annual Review of Fluid Mechanics, 43 (2011), 353–375.
(4)	日野幹雄，乱流の科学 ―構造と制御― (2020)，pp. 319–561，朝倉書店．
(5)	三好建正，“ビッグデータ同化：気象学における先端データ同化研究”，計測と制御，59巻8号（2020年8月掲載），pp. 541–545．
(6)	齋藤勇士, 野々村拓, 浅井圭介，“データ駆動型スパースセンシングのためのセンサ位置最適化”，計測と制御，59巻8号（2020年8月掲載），pp. 559–564．
(7)	Alves, M.A., Oliveira, P.J., and Pinho, F.T., “Numerical methods for viscoelastic fluid flows,” Annual Review of Fluid Mechanics, Vol. 53 (2021), 509–541.
(8)	Ronneberger, O., Fischer, P., and Brox, T., “U-Net: Convolutional networks for biomedical image segmentation”, Proceedings of International Conference on Medical Image Computing and Computer-Assisted Intervention, (2015), pp. 97–108.
(9)	田代雅哉，塚原隆裕，“粘弾性流体乱流におけるU-Netを用いた構成方程式の代理モデル構築”，日本機械学会第99期流体工学部門講演会講演論文集，（2021年11月掲載），OS01-14.
(10)	Tashiro, M. and Tsukahara, T., “DNS-CNN simulation of viscoelastic turbulent flow using U-Net”, Abstract of 15th World Congress on Computational Mechanics and 8th Asian Pacific Congress on Computational Mechanics, (2022), 1348.
(11)	塚原隆裕，川口靖夫，“乱流物質拡散源推定に向けたCNN画像認識”，日本流体力学会誌「ながれ」，38巻5号（2019年10月掲載），pp. 337–342.
(12)	Shao, Q.Q., Sekine, D., Tsukahara, T., and Kawaguchi, Y., “Inverse source locating method based on graphical analysis of dye plume images in a turbulent flow,” Open Journal of Fluid Dynamics, Vol. 6, No. 4 (2016), 72622.
(13)	Kurihara, T., Ishigami, T., and Tsukahara, T., “Regression-type inverse estimation by CNN to identify a scalar source in turbulent channel flow,” Proceedings of the 8th Asian Symposium on Computational Heat Transfer and Fluid Flow, (2021), ASCHT2021-266.
(14)	Szegedy, C. et al., “Going deeper with convolutions.” Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, (2015), pp. 1–9.
(15)	Ishigami, T., Irikura, M., and Tsukahara, T., “Machine learning to estimate the mass-diffusion distance from a point source under turbulent conditions,” Processes, Vol. 10, Issue 5 (2022), 860.