流れ　2022年11月号　目次

―　特集テーマ：2022年度年次大会　― 巻頭言 （森，金川） 壁面乱流の工学的モデリング 須賀 一彦 (大阪公立大学) 粉粒体の流れを予測する 田中 敏嗣 (大阪大学) 人工知能をメタモデルとした流体機械の最適化設計 坂口 大作 (長崎大学) 粘弾性流体や乱流拡散を対象とした深層学習 塚原 隆裕 (東京理科大学) モード分解を用いた流体計測の高度化 野々村 拓 (東北大学) 　｜　リンク一覧にもどる　｜

 

粉粒体の流れを予測する

田中 敏嗣 大阪大学

　1.　はじめに

　「流れ」を研究する対象は気体や液体だけではない．砂時計の砂も流れる．砂時計の中を重力で落下する砂粒の運動を考えると（Fig. 1），砂時計の上部に堆積している粉粒体にできたすり鉢状の斜面を砂粒は滑り落ち，オリフィスを通過して下部の砂山に落下した砂粒はなだれを起こしながら砂山を作る．このように砂時計の中では固体粒子の集合体としての粉粒体は，相転移を起こしながら固気液三相の状態を示す．粉粒体の挙動だけでも十分複雑であるが，周囲の気体と連成して流れる固気二相流になるとさらに複雑な挙動を示す．たとえば，粉粒体を蓄えた容器の下部から気流を流入させ，流体力により粉粒体を流動化させる流動層では，Fig.2に示すように高濃度の粒子層中に気泡が形成して流動化する．

　このような粉粒体の挙動は，他の力学分野の現象と同様に，数値シミュレーションによる現象の解明や予測の対象であり，様々な取り組みが行われている⁽¹⁾．ここでは，粉粒体および粒子系混相流の数値シミュレーションの概略と著者らのグループの最近の取り組みについて紹介する．

Fig.1 Flowing sand in hourglass

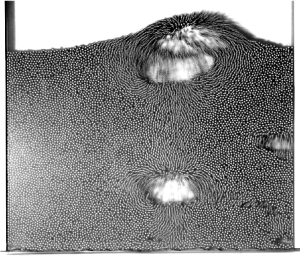
Fig.2 Bubbles formed in fluidized bed

2.　いくつかのモデル化の視点

　粉粒体の力学的挙動を数値シミュレーションする際に用いられるモデルには，個々の粒子の挙動をラグランジュ的に追跡する離散粒子モデルと，粒子群の集合体を一種の連続体としてモデル化する連続体モデルがある．粉粒体は粒径分布や形状，付着性など多様な個性を有するため，一般的に利用可能な連続体モデルの開発は発展途上の状況にある．このため，現在，産業応用も含めて広く利用されているのは離散粒子モデルである．離散粒子モデルには粒子間の相互作用を衝突でモデル化するものと接触力でモデル化するものがあるが，砂時計の中の粉粒体のように固気液三相の状態をすべて表現できるFig. 3に示すような接触力モデルを用いる離散要素法（Discrete Element Method，以後DEM）⁽²⁾が広く利用されている．以後，粉粒体のDEMシミュレーションについて述べる．

　流体・固体混相流にDEMを用いる場合，流体運動の取り扱いについては粒子スケールに対する解像度の観点から，粒子（サブ）スケール解像型のものと，粒子スケールに比べて大きなスケールで局所平均化された流れの基礎式⁽³⁾をカップリングさせて解く手法がある^(4,5)．後者の手法によりFig. 2に示すような気泡が良好に表現できる^(4,5)．

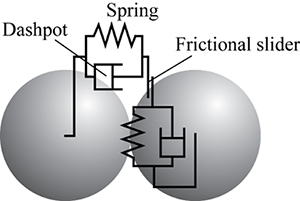
Fig.3 Contact force model of discrete element method

3.　各種モデリングおよび各種現象のシミュレーション

　一般的に工学的興味の対象となる粉粒体の挙動では粒子の数は膨大なものとなり，DEMを用いた数値シミュレーションは非常に計算負荷の大きなものとなる．このため，多くの問題において何らかの計算負荷の低減が必要となる．計算負荷の低減手法としてまず多く用いられる手法は接触力モデル中のバネ定数（剛性）の低減である．DEM計算では，接触力モデルと粒子質量から振動計の固有振動周期に比べて小さな時間刻みをとる必要があるため，バネ定数を低減することで時間刻みを大きく設定することができる．バネ定数の低減は粒子間衝突時間を増大させるが，流動状態においてはほとんどの粒子が二体衝突による粒子間相互作用を行うため，ある程度までの計算負荷の低減が可能である．しかし，粒子に付着性がある場合にはバネ定数の低減は付着の効果を強調する結果となるため，この効果を打ち消すモデリングが必要となる^(6,7)．

　計算負荷を低減するもう一つの手法は，オリジナル粒子よりも大きな粒子によりシミュレーションを行う粗大粒子モデルを用いることである．Fig.4は粗大粒子モデルを用いた粒子混合器内での粒子挙動のシミュレーション結果である⁽⁸⁾．ここでは，液が添加されており粒子間には液架橋によるキャピラリ力が働いている．粗大粒子に働く力に関して提案されたスケーリング則により，オリジナル粒子挙動が良好に表現されている．同様のスケーリング則は，粒子表面付着力や潤滑力といった様々な種類の力についても適用することが可能である．

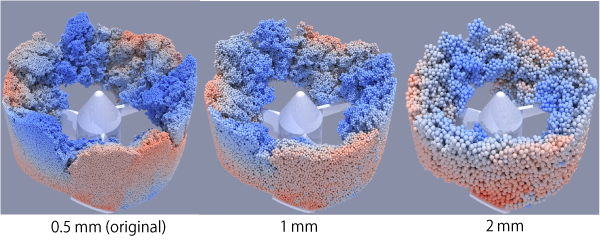
Fig.4 Motion of particles with capillary force in mixer⁽⁸⁾

　Fig.5に流動層内における粗大物体の挙動のシミュレーション結果を示す⁽⁹⁾．このような状況設定は，例えば流動層ゴミ焼却炉におけるゴミの挙動解析に関して興味の対象となる．この計算では，流体流れ計算において流動化媒体である粉粒体の粒径スケールは解像せず，一方，粗大物体まわりの流れを解像する大規模物体のモデル化⁽¹⁰⁾が用いられている．また，流動層ゴミ焼却炉のような応用に対しては物体形状の影響も重要な問題となり，Super-Ellipsoidモデルにより非球形の影響がモデル化されている．

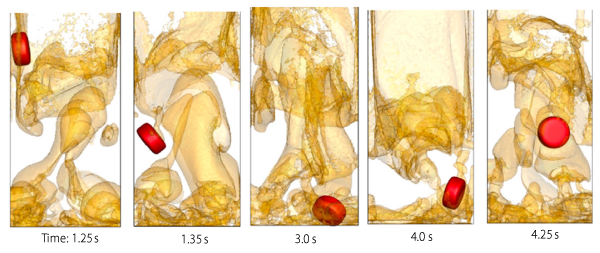
Fig.5 Motion of non-spherical large object in fluidized bed⁽⁹⁾

文　　　献

(1)	田中敏嗣, 粒子の流れ, 機械学会誌, Vol. 116, No. 1136 (2013), pp. 466-469.
(2)	Cundall, P.A. and Strack O.D.L., Discrete Numerical Model for Granular Assemblies, Geotechnique, Vol. 29 (1979), pp. 47-65.
(3)	Anderson, T. B., and Jackson R. A., Fluid Mechanical Description of Fluidized Bed, I&EC Fundamentals, Vol. 6 (1967), pp. 527-539.
(4)	川口寿裕, 田中敏嗣, 辻 裕, 離散要素法による流動層の数値シミュレーション(噴流層の場合), 日本機械学会論文集(B編), Vol. 58, No. 551 (1992), pp. 2119-2125.
(5)	Tsuji, Y., Kawaguchi, T. and Tanaka, T., Discrete Particle Simulation of Two-Dimensional Fluidized Bed, Powder Technology, Vol. 77 (1993) , pp. 79-87.
(6)	Kobayashi, T., Tanaka, T., Shimada, N., Kawaguchi, T., DEM-CFD Analysis of Fluidization Behavior of Geldart Group A Particles Using a Dynamic Adhesion Force Model, Powder Technology, Vol. 248 (2013), pp. 143-152.
(7)	Washino, K., Chan, E.L., Tanaka, T., DEM with attraction forces using reduced particle stiffness, Powder Technology, Vol.325 (2018), pp. 202-208.
(8)	Hu, Y., Chan, E.L., Tsuji, T., Tanaka, T., Washino, K., Geometry similarity on interparticle force evaluation for scaled-up DEM particles, Powder Technology, Vol. 404 (2022), 117483.
(9)	Tsuji, T., et al., FPM-SE: a numerical model for dense gas-solid flows with large non-spherical object, Chemical Engineering Science, Vol. 264 (2022), 118149.
(10)	Tsuji, T., Higashida, K., Okuyama, Y., Tanaka, T., Fictitious Particle Method: A Numerical Model for Flows Including Dense Solids with Large Size Difference, AIChE Journal, Vol.60 (2014), pp. 1606-1620.