流れ 2022年2月号 目次
― 特集テーマ: 流体工学部門講演会 2月号 ―
| リンク一覧にもどる | |
セルロース分散流中のナノ繊維静電配向に関する数値シミュレーション
薄井 拓巳 |
1. 緒 言
2021年11月8日から10日の3日間にわたり開催された第99期日本機械学会流体工学部門講演会において,栄えある優秀講演表彰をいただいた.この場を借りて日本機械学会の皆様および選考委員会の皆様に御礼を申し上げるとともに,講演発表内容を以下に紹介する.
持続可能な社会の実現に向けて,植物由来の低環境負荷・循環型材料に対する需要は年々高まっている.その材料の一つにセルロースナノファイバー(CNF)が挙げられる.CNFは高い剛性と低い熱膨張率という優れた機械的・熱的特性を有する.このように優れた特性を有するCNFは,自動車部材,ガスバリア材,医療用材料など幅広い分野での応用が期待されている.天然の木材繊維の比強度・比弾性係数は,繊維の長軸と内部に存在するCNFが成す平均角度の減少に伴って増加する(1).そのため,CNFから成るセルロース単繊維の高強度化においては単繊維のCNF配向制御が重要となる.CNFの配向が揃った高強度の木材繊維を工学的に実現する方法として,電場印加型フローフォーカシング法が提案されている(2),(3).CNFが水中に分散したCNF-水分散系において交流電場を印加した際には,CNFは電場と平行に配向することが明らかとなっており,これにより創製繊維の材料特性が著しく向上することが実験から示されている(3).
本研究では,CNFを再合成することによって得られるセルロース単繊維の高強度化を実現するために,電場印加型フローフォーカシング法におけるCNFの電場応答特性ならびに繊維形成過程における繊維配向特性を数値シミュレーションにより明らかにする.
2. 支配方程式
本研究ではCNFを長楕円体かつ剛体であると仮定し,個々のCNFの回転運動と並進運動を解析した.CNF濃度は十分に低く,流れ場に影響を与えないものとし,CNF間の相互作用は考慮していない.まず,三次元数値流動場解析によりフローフォーカシング流路内の速度場を求めた.計算手法としてSIMPLE法を用い,自由表面解析にLevel-Set法およびVOF法を用いて計算を行った.流路は図1に示すように1 mm×1 mmの矩形断面を有し,主流上端からシース流上壁までの距離は22 mm,シース流流路長は3 mmとした.このときの主流の流量は実験条件を参照してQ1 = 6.5 mm3/s,シース流の流量はQ2/2 = 3.75mm3/sである.また,主流上端から4 mmの位置において流路上壁および下壁上に一対の電極が存在し,軸方向の電極幅および電極間隔はそれぞれ2 mmおよび8 mmである.なお,電極はCNF-水分散系に直接接している.得られた流れ場を用い,以下のCNFに対する回転と並進に関する運動方程式を解くことにより,CNFの流動場における三次元空間での複雑挙動を解析した.
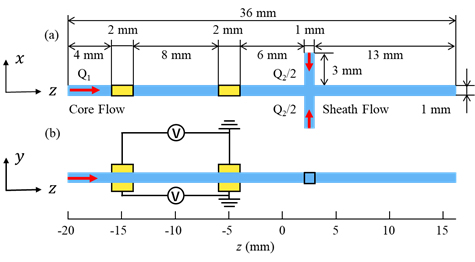
Figure 1 Schematic illustration of the channel (a) top view, (b) side view.
2・1 回転運動に関する運動方程式
繊維の回転に関する運動方程式を以下に示す.
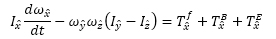 |
(1) |
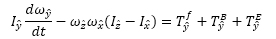 |
(2) |
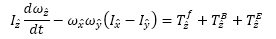 |
(3) |
上式中のT f,T B,T Eはそれぞれ粘性およびブラウン運動,静電配向によるトルクである.座標系の定義は楕円粒子の長軸および短軸に沿ったものとし,\(\hat{x}\), \(\hat{y}\)を短軸方向,\(\hat{z}\)を長軸方向としている.電場分布は電位に関するラプラス方程式を解くことにより求めた.粘性,ブラウン運動および静電配向による回転軸回りのトルクはそれぞれ以下のように与えられる(4).
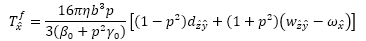 |
(4) |
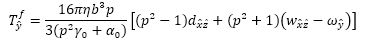 |
(5) |
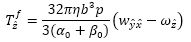 |
(6) |
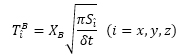 |
(7) |
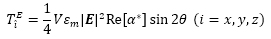 |
(8) |
ここで,ηは溶媒(水)の粘度,bは繊維幅,pはCNFのアスペクト比,α0,β0およびγ0は繊維の形状パラメータ,d\(\hat{i}\hat{j}\) はひずみテンソル,w\(\hat{i}\hat{j}\) は渦度テンソル,XBはボックス・ミュラー法により生成された乱数,I\(\hat{l}\)は軸回りのモーメント,S\(\hat{l}\)は各スペクトル強度,V はCNFの体積,Eは電界ベクトル,θは繊維と電界の成す角,α*は分極係数である.
2・2 並進運動に関する運動方程式
繊維の並進に関する運動方程式を以下に示す.
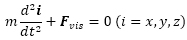 |
(9) |
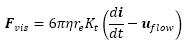 |
(10) |
なお,並進運動においては粘性抵抗力のみを外力として考慮した.なお,式中のreは楕円の等価半径,Ktは並進運動における抵抗係数である.式(1)-(3),(9)を4次のルンゲ=クッタ法で解いた.本研究における繊維幅は20 nmで一定とし,繊維長は600,900,1200および2000 nmのそれぞれ単一繊維長とした.本研究では1000個の粒子(繊維)を対象とし計算の初期においては,シース流合流部から20 mm上流の位置において図2に示すように,左右壁面から0.4 mm,上下壁面から0.1 mm離れた0.2×0.8 mmの領域に粒子を配置する.なお,粒子の初期位置および初期角度は乱数により与えた.
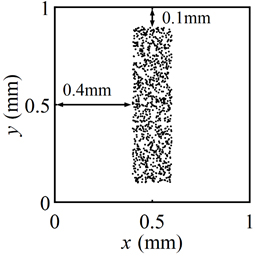
Figure 2 Initial fibrils distribution on x-y plane.
3. 結果と考察
3・1 伸長流動場解析
図3は,三次元数値シミュレーションによって得られた伸長流領域でのVOF関数分布を示す.VOF関数は0から1の値をとり(CNF-水分散系を1とし,水相を0とする),VOF関数が0.5の値となる位置をCNF-水分散系と水との疑似界面と定義する.また,シース流上壁から2 mm上流の位置を原点として示している.図よりシース流上壁から約4 mm下流(z = 6 mm)の位置においてCNF-水分散系は流路の壁面から剥離し,液糸を形成することが分かる.
図4に流路中心軸上における流速分布を実験値(5)と比較して示す.主流とシース流が合流した後 z = 6 mmにおいてCNF流が壁面から剝離することにより,CNF流は12 mm/sから20 mm/sまで加速し,z = 8 mm以降においては液糸形状が定常となり,CNF-水分散系の断面形状がほぼ一定となることからほぼ一定の速度となる.得られた流速分布はドップラー法による速度計測結果(5)と良い一致が見られ,本計算結果の妥当性が評価できる.
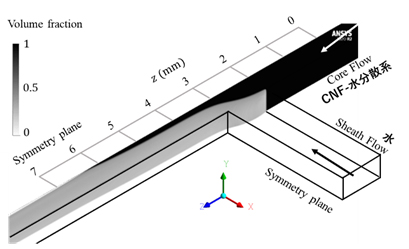
Figure 3 Volume fraction of CNF dispersion in flow-focusing channel.
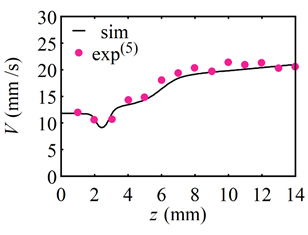
Figure 4 Comparison of velocity distribution along the centerline between numerical simulation and experimental results.
3・2 繊維長が繊維配向に与える影響
図5は流路上流部における電場分布を示す.電場はx方向に対してほぼ一様であり,ここではx = 0.5 mmにおけるy-z平面上での電場分布を示している.電極角部における電界集中のために,局所的に高い電場が生じているものの,流路中心部においては一様な電界が形成されている.
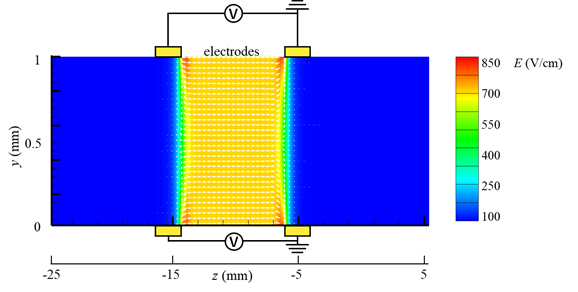
Figure 5 Electric field distribution in y-z plane at x = 0.5 mm.
動画1は1000個の粒子が流路上流から流れている様子を可視化したものである.なお,このときの繊維長は900 nmとし,印加電圧は600 Vである.それぞれの繊維について,y-z平面に射影した角度に応じて色を変化させている.電場領域およびシース流の合流部近傍において0°近傍の繊維が増えていることが分かり,電場およびせん断・伸長流効果により繊維配向が促進する.
Movie 1 Visualization of fiber alignment by electric and flow fields (V = 600V, l = 900 nm).
図6は流路中における繊維の配向度を電場の有無で比較したものである.ここで,繊維配向度とは繊維の長軸(\(\hat{z}\)軸)とz軸とのなす角φから以下の式を用いて評価される(1).なお,配向度Sは繊維配向が完全にランダムの場合に0となり,完全配向の場合において1となる.配向分布関数I(φ)はガウス分布に従うと仮定し,任意の位置における1000個の繊維群の平均繊維角μと分散値σから式(12)により求められる.
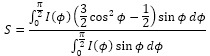 |
(11) |
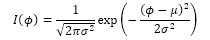 |
(12) |
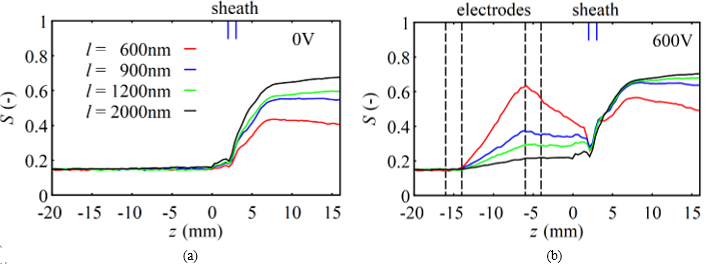
Figure 6 Effect of applied electric field on CNF alignment for (a) V = 0 V and (b) V = 600 V.
図6(a)より,電場を印加しない場合いずれの繊維長に対しても,シース流が流入するz = 2 mmの位置において配向度が上昇しており,伸長流によって生じるせん断・伸長効果により配向することが分かる.また,このとき長い繊維ほど高い配向度を示す.一方,電場を印加した場合,図6(b)より,短い繊維ほど電場応答性が高く,電場印加領域では高い配向度が得られるが,電場領域下流(z = -6 mm ~ 2 mm)においては,ブラウン運動の影響がより支配的となり,配向度が急激に低下する.
図7はシース流下流壁から7 mm下流(z = 10 mm)での繊維群の配向度を電場の有無に対して比較して示したものである.先に述べたように無電場時では長い繊維ほど高い配向度が得られることが分かる.電場を印加した場合,いずれの繊維長に対しても配向度の向上効果が得られた.また,配向度の向上率は短繊維ほど高く,600 nmの繊維群では25.7 %の向上が得られる.900 nmの繊維においては,電場を印加することにより無電場時での2000 nmとほぼ同等の高い配向度が得られることが明らかとなり,短い繊維であっても電場を印加することにより十分に高い配向度が得られることが示された.
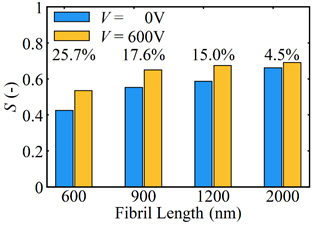
Figure 7 Obtained order parameter at z = 10 mm for different fibril length with or without electric field.
4. 結 言
本研究では,電場印加型フローフォーカシング法を用いてCNFを再合成することによって得られるセルロース単繊維の高強度化を実現するため,CNF配向に与える電場印加効果を数値シミュレーションにより明らかにした.
- 無電場においては,伸長流による配向効果により,長いCNF繊維ほど高い配向度が得られる.
- 電場を印加した場合,いずれの繊維長に対しても配向度の向上効果が得られる.また,電場による配向度の向上率は短繊維ほど高く,短繊維であっても無電場での長繊維とほぼ同等の配向度が得られる.



